MATLAB教学_06进阶绘图
本文学习视频:https://www.bilibili.com/video/av68228488?p=6
本文学习内容:
- 进阶2D绘图
- 绘图空间
- 3D绘图
semilogx(x,y); %x轴取对数
semilogy(x,y); %y轴取对数loglog函数
%%
clc;
clear all;
x=logspace(-1,1,100); %从10^{-1}到10^1,取100个字
y=x.^2;
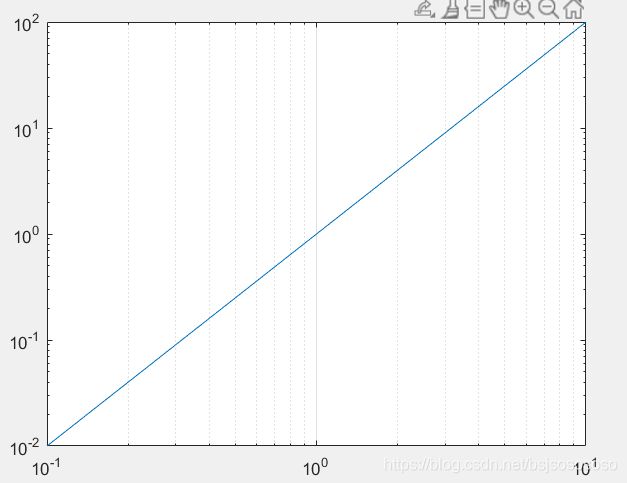
loglog(x,y); %X轴和Y轴都取对数
set(gca,'Xgrid','on'); %因为可以看到X和Y的距离不一样,所以最好打开网格。plotyy()函数
有关plotyy()函数的的帮助文件
[AX,H1,H2] = plotyy(___) returns the handles of the two axes created in AX and the handles of the graphics objects from each plot in H1 and H2. AX(1) is the left axes and AX(2) is the right axes.
plotyy()函数会有3个句柄,实际可以理解为4个。第一个AX,创建两个轴的句柄,而H1和H2是每个绘图的图形对象的句柄。AX(1)是左坐标轴,AX(2)是右坐标轴。
clear;
clc;
x=0:0.01:20;
y1=200*exp(-0.05*x).*sin(x);
y2=0.8*exp(-0.5*x).*sin(10*x);
[AX H1 H2]=plotyy(x,y1,x,y2);
set(get(AX(1),'Ylabel'),'String','Left Y-axis'); %这里是先提取AX(1)里的 Ylabel,再设置
set(get(AX(2),'Ylabel'),'String','Right Y-axis');
title('Labeling plotyy');
set(H1,'LineStyle','--');
set(H2,'LineStyle',':','Color',[1 0 1]);
在MATLAB帮助文件中,可以看到:
不推荐使用plotyy()函数,而是推荐使用 yyaxis()函数。因此以上程序 可以改写为:
clear;
clc;
x=0:0.01:20;
y1=200*exp(-0.05*x).*sin(x);
y2=0.8*exp(-0.5*x).*sin(10*x);
yyaxis left %先设置左边Y轴的信息
plot(x,y1,'--');
ylabel('Left Y-axis');
hold on
yyaxis right %设置右边Y轴的信息
plot(x,y2,':r');
ylabel('Right Y-axis');
title('Labeling plotyy');Histogram() 直方图
这个函数MATLAB不推荐使用,
clear;
y=randn(1,1000); %成生一个1 *1000 的符号正态随机的矩阵
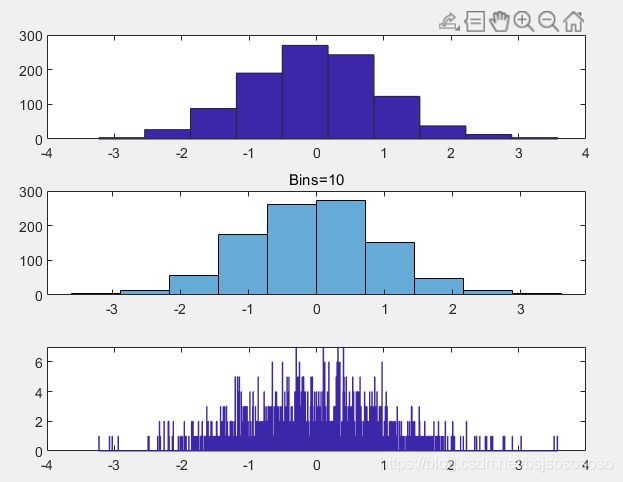
subplot(3,1,1);
hist(y,10); %分成10个BIN,Y轴表示在每个BIN中的元素个数
subplot(3,1,2);
histogram(y,10);
title('Bins=10');
subplot(3,1,3);
hist(y,1000);bar()
bar( 创建一个条形图,y)y 中的每个元素对应一个条形。如果 y 是矩阵,则 bar 根据 y 中的行对条形分组。
x=[1 2 5 4 8]; y=[x;1:5];
subplot(1,3,1); bar(x); %x 中的每个元素对应一个条形。
subplot(1,3,2); bar(y); %y 中的每个元素对应一个条形。如果 y 是矩阵,则 bar 根据 y 中的行对条形分组。
subplot(1,3,3); bar3(y); %会生成三维图
x=[1 2 5 4 8]; y=[x;1:5];
subplot(1,3,1); bar(y,'stacked');
title('stacked');
subplot(1,3,2); bar(y,'histc');
title('histc');
subplot(1,3,3); bar(y,'hist');
title('hist');可以用不同的属性让bar()函数显示不同的图形
演示如下:
17分钟练习
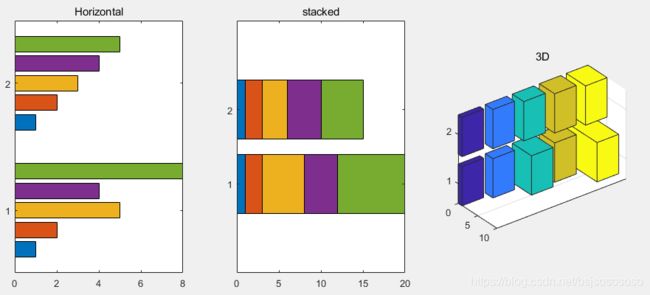
x=[1 2 5 4 8]; y=[x;1:5];
subplot(1,3,1);
barh(y);
title('Horizontal');
subplot(1,3,2);
barh(y,'stacked');
title('stacked');
subplot(1,3,3);
bar3h(y);
title('3D');
Pie Charts() 函数
pie( 将扇区从饼图偏移一定位置。X,explode)explode 是一个由与 X 对应的零值和非零值组成的向量或矩阵。pie 函数仅将对应于 explode 中的非零元素的扇区偏移一定的位置。
如果 X 为 categorical 数据类型,则 explode 可以是由对应于类别的零值和非零值组成的向量,或者是由要偏移的类别名称组成的元胞数组。
通过将对应的 explode 元素设置为 1 来偏移第饼图扇区。
clear; % 18分钟练习
a=[10 5 20 30];
subplot(2,2,1); pie(a);
subplot(2,2,2); pie(a,[0 0 0 1]);
subplot(2,2,3); pie3(a,[0 0 0 1]);
subplot(2,2,4); pie(a,[1 1 1 1]);Polar Chart
polar 函数接受极坐标,对这些数据在笛卡尔平面中绘图,并在平面上绘制极坐标网格。
polar(theta,rho) 创建角 theta 对半径 rho 的极坐标图。theta 是从 x 轴到半径向量所夹的角(以弧度单位指定);rho 是半径向量的长度(以数据空间单位指定)。
polar(theta,rho,LineSpec) LineSpec 指定线型、绘图符号以及极坐标图中绘制线条的颜色。
polar(axes_handle,...) 将图形绘制到带有句柄 axes_handle 的坐标区中,而不是当前坐标区 (gca) 中。
h = polar(...) 返回 h 中的线条对象。
不过MATLAB不推荐使用些函数,改用如下:
polarplot( 在极坐标中绘制线条,由 theta,rho)theta 表示弧度角,rho 表示每个点的半径值。输入必须是长度相等的向量或大小相等的矩阵。如果输入为矩阵,polarplot 将绘制 rho 的列对 theta 的列的图。也可以一个输入为向量,另一个为矩阵,但向量的长度必须与矩阵的一个维度相等。
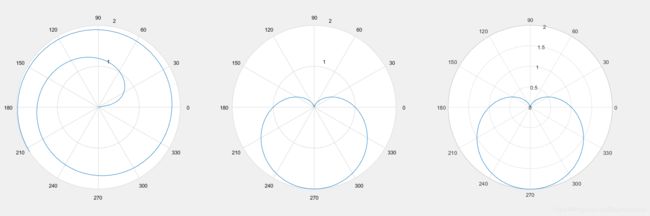
clear; %20分钟
x=1:100; theta=x/10; r=log10(x);
subplot(1,3,1); polar(theta,r);
theta=linspace(0,2*pi); r=1-sin(theta);
subplot(1,3,2); polar(theta,r);
subplot(1,3,3); polarplot(theta,r);
六边形的练习
%%
clear; %20分钟
theta=linspace(0,2*pi,7);
r=ones(1,length(theta));
subplot(1,3,1);polarplot(theta,r);
theta=linspace(0,2*pi,6); r=ones(1,length(theta));
subplot(1,3,2); polar(theta,r);
subplot(1,3,3);
r=[ones(1,length(theta))*2] %将半径变大,则图形也变大
polarplot(theta,r);
22分钟练习_六边形
%%
clear; %22分钟,6边形
theta=linspace(0,2*pi,7); %先用linspace产生6个点。每个点对应到角度到上就相当于5条向外发射的线
r=ones(1,length(theta)); % 用ones产生长度为1的length(theta)个1,这里length(theta)就是在MATLAB教学02里讲的矩阵里较为大的行或列,这里是列,所以为6
subplot(1,2,1);
polarplot(theta,r);
subplot(1,2,2);
r=[ones(1,length(theta))*2] %将半径变大,则图形也变大
polarplot(theta,r);Stairs and Stem Charts
x=linspace(0,4*pi,40); y=sin(x);
subplot(1,2,1); stairs(y); %阶梯图,其中每一段都是一个X的点,这里有40个点
subplot(1,2,2); stem(y); %离散序列图阶梯图像不像数电,在某一个范围内,电压值都一样。
离散图就更像了,在某一个时间段只取一个次值。哈哈哈
22分钟练习
clear; %25分钟练习,这里感觉不对。因为plot画图时点的数量不够,
t=linspace(0,10,50); y=sin(pi*t.^2/4);
hold on
plot(t,y,'b');
stem(t,y);
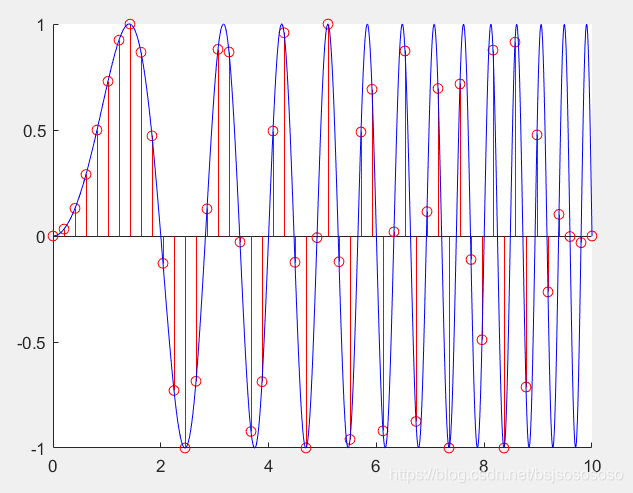
%% 25分钟练习,参看评论写的。
x1=linspace(0,10,50);
y1=sin((x1.^2)*pi/4);
x2=linspace(0,10,1000);
y2=sin((x2.^2)*pi/4);
hold on
stem(x1,y1,'r');
plot(x2,y2,'b');
ylim([-1 1]);
% get(gca,'YTick',[-1 0.5 0 0.5 1]);
yticks([-1 -0.5 0 0.5 1]);
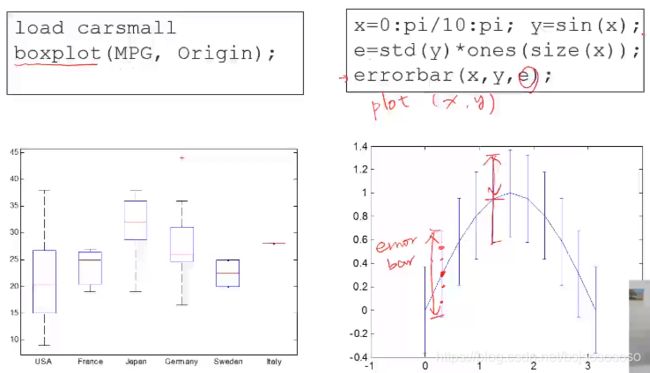
Boxplot and Error Bar
confidence interval 置信区间
error bar 误差线
这个就不懂了,好像是统计的。
fill()
clear all; %27分钟练习
clc;
t=(1:2:15)'*pi/8;
x=sin(t);
y=cos(t);
subplot(2,2,1);
plot(x,y); axis square off; box on; %用plot画了下,但是最上面的线没有
%这里用x,y,可以试着画下,就是取sin(t)和cos(t)的交点
subplot(2,2,2);
t=(1:2:19)*pi/8;
plot(x,y);axis square off; %试着把t变大,还是没看到线。疑问
subplot(2,2,3);
fill(x,y,'r');
subplot(2,2,4);
fill(x,y,'r'); axis square off; %fill就是填充函数
text(0,0,'STOP','Color','w','FontSize',38,... %文本函数
'FontWeight','bold','HorizontalAlignment','center');
%%
clear all; %画了三个图,可以看到是一个顺时针的顺序,所以上面用plot画时中间那里没线
clc;
t=[1*pi/8:pi/4:15*pi/8];
x=sin(t);
y=cos(t);
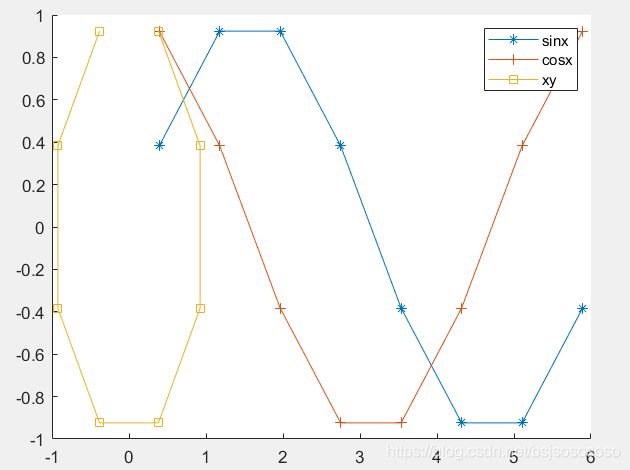
hold on
plot(t,x,'Marker','*');
plot(t,y,'Marker','+');
plot(x,y,'Marker','s');
legend('sinx','cosx','xy')这里 text()函数的有关介绍。最前面是坐标,然后后面跟所写的内容。再然后就是多组 'Name', 'Value'; 可以增加的Name 如下。
33分钟练习
clear; %33分钟练习
clc;
subplot(1,2,1);
t1=[1 0 -1 0]; t2=[0 1 0 -1]; %这个练习只有4个点,所以用矩阵更为方便
fill(t1,t2,'y'); axis square off;
text(0,0,'WAIT','FontSize',40,'FontWeight','bold','HorizontalAlignment',...
'center');
subplot(1,2,2);
t3=(0:pi/2:2*pi); %如果用cos和sin的话,也只取4个交点
x=sin(t3); y=cos(t3);
fill(x,y,'r'); axis square off;Color space
文本颜色,指定为 RGB 三元组、十六进制颜色代码、颜色名称或短名称。默认值 [0 0 0] 对应于黑色。
对于自定义颜色,请指定 RGB 三元组或十六进制颜色代码。
-
RGB 三元组是包含三个元素的行向量,其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内,例如[0.4 0.6 0.7]。 -
十六进制颜色代码是字符向量或字符串标量,以井号 (
#) 开头,后跟三个或六个十六进制数字,范围可以是0到F。这些值不区分大小写。因此,颜色代码'#FF8800'与'#ff8800'、'#F80'与'#f80'是等效的。
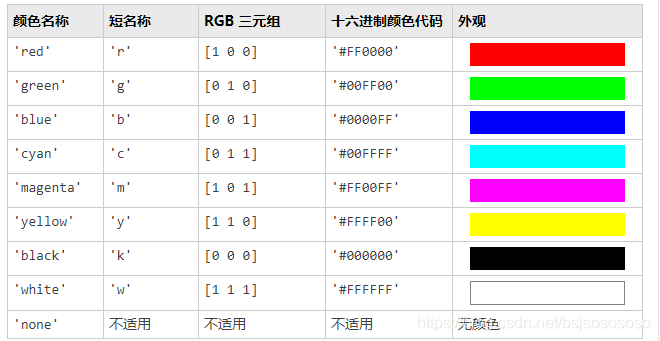
例如我们常用的一些颜色表如下:
也就是说你写一个颜色时,可以用这4个方式都可以。尤其是十六进制,是根据[ 255 255 255] 转换过来的。例如:
40分钟练习
clear all; %40分钟练习
clc;
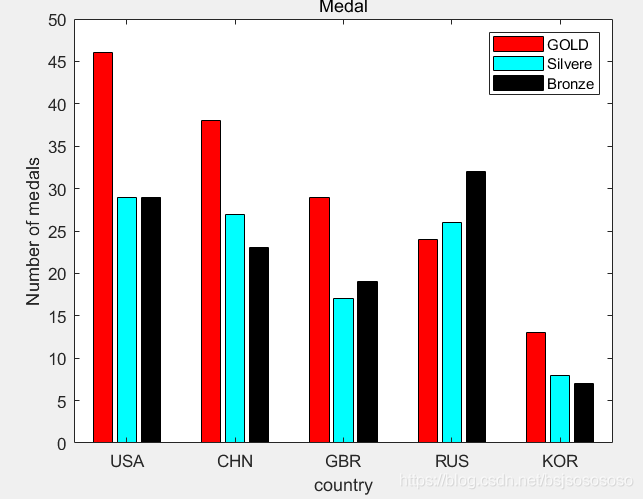
G=[46 38 29 24 13];
S=[29 27 17 26 8];
B=[29 23 19 32 7];
h=bar(1:5,[G' S' B']);
h(1).FaceColor='#FF0000';
h(2).FaceColor=[0 1 1];
h(3).FaceColor='black';
title('Medal');
ylabel('Number of medals');
xlabel('country');
legend('GOLD','Silvere','Bronze');
set(gca,'XTickLabel',{'USA' 'CHN' 'GBR' 'RUS' 'KOR'});imagesc()
[X,Y] = meshgrid(x,y)
[ 基于向量 X,Y] = meshgrid(x,y)x 和 y 中包含的坐标返回二维网格坐标。X 是一个矩阵,每一行是 x 的一个副本;Y 也是一个矩阵,每一列是 y 的一个副本。坐标 X 和 Y 表示的网格有 length(y) 个行和 length(x) 个列。例如:
surf( 创建一个三维曲面图。该函数将矩阵 X,Y,Z)Z 中的值绘制为由 X 和 Y 定义的 x-y 平面中的网格上方的高度。函数还对颜色数据使用 Z,因此颜色与高度成比例。
imagesc( 将数组 C)C 中的数据显示为一个图像,该图像使用颜色图中的全部颜色。C 的每个元素指定图像的一个像素的颜色。生成的图像是一个 m×n 像素网格,其中 m 和 n 分别是 C 中的行数和列数。这些元素的行索引和列索引确定了对应像素的中心。
clear all;
clc;
[x,y]=meshgrid(-3:0.2:3,-3:0.2:3);
z=x.^2+x.*y+y.^2;
subplot(1,2,1);
surf(x,y,z); box on; %曲面
xlim([-4 4]);
ylim([-4 4]);
subplot(1,2,2);
imagesc(z); %平面用 colorbar() 可以显示颜色条形码
49分钟练习
clear all; %49分钟练习
g=0.3;
x=[1:10; 3:12;5:14];
imagesc(x);
[m n]=size(x); %可以直接用max(max(x)) 和 min(min(x))找到最大值和最小值
max=0;
min=1000;
for i=1:m
for j=1:n
if maxx(i,j)
min=x(i,j)
end
j=j+1;
end
i=i+1;
end
map=zeros(max,3);
for i=1:14
map(i,2)=g;
g=g+0.05;
end
colormap(map);
colorbar; 这个在做颜色的时候,先是提取了X中有多少个数据 ,是30个。然后建了一个map的颜色矩阵,从第1行到30行分别设置颜色。结果最后发现老是被覆盖,而且颜色变得很乱。最后发现,原来使用colormap()函数时,它里面的颜色是根据你的这个原有数据的值去变化的,也就是比如第一行的第三个元素是3,然后第二行的第一个也是3,那么他两的颜色是一样的。而不能由map 去建立两个颜色的行。所以,修改后我先找出X里最大的值和最小的值,然后依次为这14个不同的数据建立14个颜色表就可以。
3D Plots
plot3()
clear all; % 52分钟练习
clc;
x=0:0.1:3*pi;
z1=sin(x); z2=sin(2*x); z3=sin(3*x);
y1=zeros(size(x)); y3=ones(size(x)); y2=y3./2;
plot3(x,y1,z1,'r-',x,y2,z2,'b:',x,y3,z3,'g--');
grid on; %打开网格clear all; %60分钟练习
x=-3.5:0.2:3.5; y=-3.5:0.2:3.5;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
subplot(1,2,1); mesh(X,Y,Z); %网格图
subplot(1,2,2); surf(X,Y,Z); %曲面图
clear all; %63分钟练习
x=-3.5:0.2:3.5; y=-3.5:0.2:3.5;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
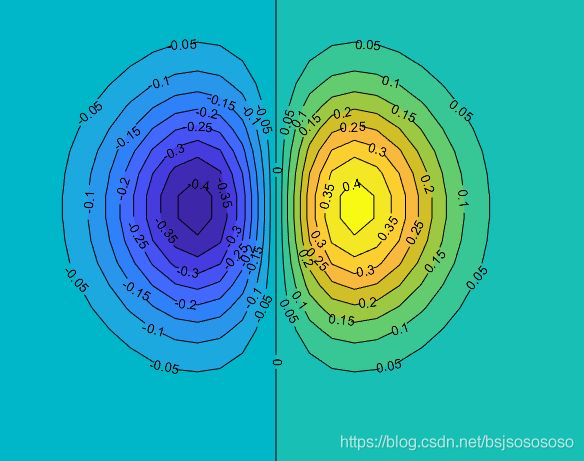
subplot(1,4,1); contour(Z);
subplot(1,4,2); contour(Z,[-0.45:0.1:0.45]); axis square;
subplot(1,4,3); [C,h]=contour(Z);
clabel(C,h);
subplot(1,4,4); contourf(Z);这里C和h是从contour() 里提取的数据 ,关于C:
等高线矩阵,返回为二行矩阵。此矩阵包含等高线层级(高度)和每个层级上各顶点的坐标。对于 n 条等高线,数据按顺序排列在 n 组列中:
-
每组中的第一列包含等高线层级和该层级上的顶点数量。顶部数字是等高线层级,底部数字是顶点数量。
-
组中的后续列是顶点的 (x, y) 坐标。每列表示一个有序对组。顶部的数字是 x 坐标,底部的数字是 y 坐标。
例如,以下是等高线矩阵 M = contour(peaks(3)) 的前几列:
关于h : 解释为等高线对象,就是每一条线,从图上看出来的每一条等高线。
从h中提取的数据可以看到。 LevelList: [-0.4000 -0.3000 -0.2000 -0.1000 0 0.1000 0.2000 0.3000 0.4000], 所以h就是等高线。每条线,可以对这些线的宽啊,颜色啊之类做改变。
64分钟练习
clear all; %64分钟练习
x=-3.5:0.2:3.5; y=-3.5:0.2:3.5;
[X,Y]=meshgrid(x,y);
Z=X.*exp(-X.^2-Y.^2);
[C,h]=contourf(Z,[-0.45:0.05:0.45]);
clabel(C,h); axis square;meshc() 和 surfc()
这个指令用法与mesh() 和 surf() 一样。
只不过底部会有影印。
View()
view(-45,20); 这里是指两个角度,其中-45度是图里的Azimuth, 从-Y轴开始逆时针旋转; Elevation是从XY平面向Z轴旋转;
关于light() 和 patch()
light()用于打光;
patch()用于画多边形;
v=[0 0 0;1 0 0;1 1 0;0 1 0;... %这里分别指的是8个顶点里下面4个顶点的坐标;
0.25 0.25 1;0.75 0.25 1;0.75 0.75 1;0.25 0.75 1]; %这里分别指的是8个顶点里上面4个顶点的坐标;
f=[1 2 3 4; %这里指的是面的连接,将第1个顶点与第2个相连,2与3连,3与4连,下面相同
5 6 7 8;
1 2 6 5;
2 3 7 6;
3 4 8 7;
4 1 5 8];
subplot(1,2,1);
patch('Vertices',v,... %顶点坐标
'Faces',f,... %定义每个面的顶点连接
'FaceVertexCData',hsv(6),... %属性是面和顶点颜色,hsv(m) 是产生包含m 个颜色的颜色图
'FaceColor','flat'); %面颜色,对于插值颜色,请将此属性指定为 'interp'。对于统一颜色,请将此属性指定为 'flat'。
view(3); axis square tight; grid on;patch()函数的设置很复杂,大家可以看MATLAB的帮助文件,如下:
https://ww2.mathworks.cn/help/matlab/ref/matlab.graphics.primitive.patch-properties.html#buduav0-1-Faces
Exercise
load cape
X=conv2(ones(9,9)/81,cumsum(cumsum(randn(100,100)),2)); %这里用的是full类型的二维卷积,cumsum是反回这个随机矩阵中每列的累积和的矩阵。2是第二个维度计算。矩阵的行中的连续元素进行求和并返回一个包含每行累积和的列向量。
surf(X,'EdgeColor','none','EdgeLighting','Phong','FaceColor','interp');
colormap(map);
caxis([-10,300]);
grid off;
axis off;最后一个完全看不懂哦,就感觉很牛逼 !!