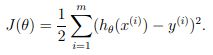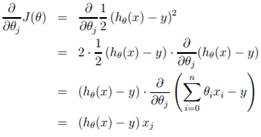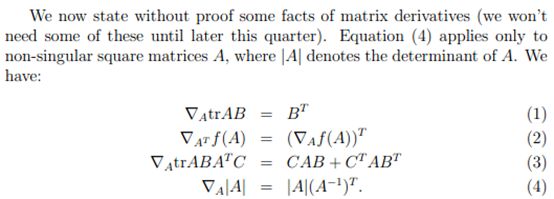机器学习第一课
由于最近在学习standford大学 Andrew Ng 大牛的机器学习视频,所以想对所学的方法做一个总结,后面所要讲到的算法主要是视频里面学到的机器学习领域常用的算法。在文中我们所要学的的算法主要有Linear Regression(线性回归),gradient descent(梯度下降法),normal equations(正规方程组),Locally weighted linear regression(局部加权线性回归)。由于开始研究mechine learning 的知识,所以之前的JAVA和C++,ACM学习暂时告一段落,同时由于方便以后写论文的需要,文中的一些专业术语会使用英文。希望和大家多多学习,交流,祝大家“国庆节快乐~”
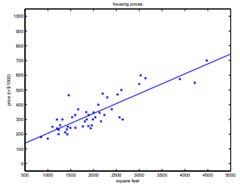
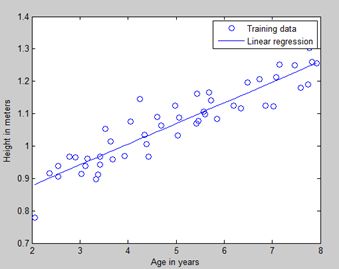
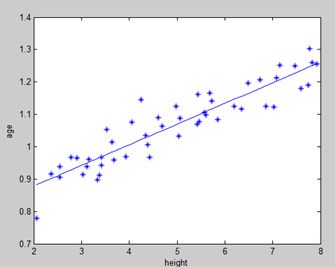
我们来学习线性回归。在高中的时候我们都已经接触到了Linear Regression的思想。(如下图所示)
给定一系列的点,需要我们拟合一条直线对所有点的位置进行一个预测,这种模型就称之为Linear Regression,所拟合出的直线是连续的直线。如果我们没给出一个input对应的直线上面都会给出一个output。好接下来我们的问题就来了,给我们一组数据我们怎样才能准确的拟合出这一条直线呢。最常用的方法有两个:1.gradient descent和2.rmal equations,其实这两种方法蕴含的思想是一样的,只不过normal equations是gradient descent在某些特殊情况下推导出来的一个我们直接可以用的方程组,下面我们会具体讨论。
来我们来讨论其数学模型,假定我们有一个input(x1, x2)代表两种特征。给定θ(θ1,θ2)对应的是每种特征的权值,![]() 是我们的预测output,即:
是我们的预测output,即:
定义cost function(损失函数)为:
式中我们可以看到,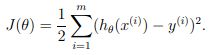 是一个二次函数,而梯度下降法正是一种对二次函数进行迭代从而求minimum value的方法。下面我们来讲怎么用gradient descent求解cost function 的minimum value,我们给出下式:
是一个二次函数,而梯度下降法正是一种对二次函数进行迭代从而求minimum value的方法。下面我们来讲怎么用gradient descent求解cost function 的minimum value,我们给出下式:
其中 ![]() 是每次迭代更新后的参数向量,
是每次迭代更新后的参数向量,![]() 是学习率(每次迭代的步长),
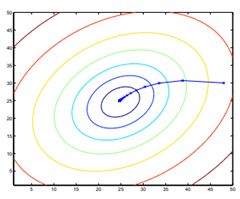
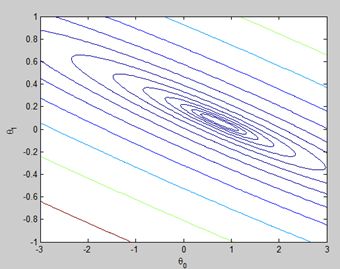
是学习率(每次迭代的步长),![]() 指cost function对参数求偏导,由高数知识可知,偏导对应的就是梯度方向,也就是参数变化最快的方向,这样我们通过不断的迭代直至函数收敛就可以求出minimu value。如下图所示(梯度等高线):
指cost function对参数求偏导,由高数知识可知,偏导对应的就是梯度方向,也就是参数变化最快的方向,这样我们通过不断的迭代直至函数收敛就可以求出minimu value。如下图所示(梯度等高线):
沿着箭头方向不断的下降就可以求出最小值,值得注意的是,如果所求的cost function不是“凸函数”,有多个极值,我们可能陷入“局部最优”。而且根据数学公式的推导,梯度越往后迭代下降的越慢(怎么推导的我也没弄明白,反正大牛是这么说的)。
到此我们就几乎将gradient descent方法大概的讲清楚了,接下来我们来讲一下normal equations:
我们先给出正规方程组的形式:![]() 也就是我们不通过迭代直接就可以求出参数向量
也就是我们不通过迭代直接就可以求出参数向量![]() ,其中
,其中![]()
接下来是视频讲义中![]() 的推导过程,这里涉及大量数学公式,直接粘贴过来:
的推导过程,这里涉及大量数学公式,直接粘贴过来:
到此为止我们就讲最小二乘法normal equations讲完了。接下来我们简单的讲解一下Locally weighted linea regression(局部加权线性回归)。 Locally weighted linear regression是建立在Linear Regression基础上的一种非线性的线性回归的方法。其思想如下:给定一组input,我们选取每一个点的局部区域在其局部区域内利用Linear Regression求取一回归直线,组合所有局部区域求得的回归直线就是Locally weighted linear regression了。
下面是我在Matlab中对Linear Regression和Normal equations的实现:
Linear Regression:
1: clear all; close all; clc
2: x = load('ex2x.dat'); y = load('ex2y.dat');
3:
4: m = length(y); % number of training examples
5:
6:
7: % Plot the training data
8: figure; % open a new figure window
9: plot(x, y, 'o');
10: ylabel('Height in meters')
11: xlabel('Age in years')
12:
13: % Gradient descent
14: x = [ones(m, 1) x]; % Add a column of ones to x
15: theta = zeros(size(x(1,:)))'; % initialize fitting parameters
16: MAX_ITR = 1500;
17: alpha = 0.07;
18:
19: for num_iterations = 1:MAX_ITR
20: % This is a vectorized version of the
21: % gradient descent update formula
22: % It's also fine to use the summation formula from the videos
23:
24: % Here is the gradient
25: grad = (1/m).* x' * ((x * theta) - y);
26:
27: % Here is the actual update
28: theta = theta - alpha .* grad;
29:
30: % Sequential update: The wrong way to do gradient descent
31: % grad1 = (1/m).* x(:,1)' * ((x * theta) - y);
32: % theta(1) = theta(1) + alpha*grad1;
33: % grad2 = (1/m).* x(:,2)' * ((x * theta) - y);
34: % theta(2) = theta(2) + alpha*grad2;
35: end
36: % print theta to screen
37: theta
38:
39: % Plot the linear fit
40: hold on; % keep previous plot visible
41: plot(x(:,2), x*theta, '-')
42: legend('Training data', 'Linear regression')%标出图像中各曲线标志所代表的意义
43: hold off % don't overlay any more plots on this figure,指关掉前面的那幅图
44:
45: % Closed form solution for reference
46: % You will learn about this method in future videos
47: exact_theta = (x' * x)\x' * y
48:
49: % Predict values for age 3.5 and 7
50: predict1 = [1, 3.5] *theta
51: predict2 = [1, 7] * theta
52:
53:
54: % Calculate J matrix
55:
56: % Grid over which we will calculate J
57: theta0_vals = linspace(-3, 3, 100);
58: theta1_vals = linspace(-1, 1, 100);
59:
60: % initialize J_vals to a matrix of 0's
61: J_vals = zeros(length(theta0_vals), length(theta1_vals));
62:
63: for i = 1:length(theta0_vals)
64: for j = 1:length(theta1_vals)
65: t = [theta0_vals(i); theta1_vals(j)];
66: J_vals(i,j) = (0.5/m) .* (x * t - y)' * (x * t - y);
67: end
68: end
69:
70: % Because of the way meshgrids work in the surf command, we need to
71: % transpose J_vals before calling surf, or else the axes will be flipped
72: J_vals = J_vals';
73: % Surface plot
74: figure;
75: surf(theta0_vals, theta1_vals, J_vals)
76: xlabel('\theta_0'); ylabel('\theta_1');
77:
78: % Contour plot
79: figure;
80: % Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
81: contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 2, 15))%画出等高线
82: xlabel('\theta_0'); ylabel('\theta_1');%类似于转义字符,但是最多只能是到参数0~9
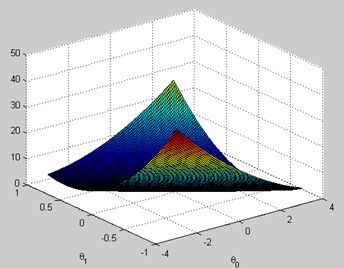
三幅图依次是:回归直线,损失函数,等高线。
Normal equations:
1: %%方法一 使用Normal Equations方法
2: clear all;
3: clc;
4: addpath('ex2Data');
5:
6: x = load('ex2x.dat');
7: y = load('ex2y.dat');
8: plot(x,y,'*')
9: xlabel('height')
10: ylabel('age')
11: x = [ones(size(x),1),x];
12: w=inv(x'*x)*x'*y %Normal Equations
13: hold on
14: %plot(x,0.0639*x+0.7502)
15: plot(x(:,2),0.0639*x(:,2)+0.7502)%更正后的代码
这是Normal equations 得到的直线,可以看出两种方法得到的直线几乎是一样的。