2020第十一届蓝桥杯国赛C/C++b组总结（填空题）

2020第十一届蓝桥杯国赛C/C++b组总结

试题 A: 美丽的 2
本题总分:5 分

【问题描述】
小蓝特别喜欢 2,今年是公元 2020 年,他特别高兴。
他很好奇,在公元 1 年到公元 2020 年(包含)中,有多少个年份的数位中包含数字 2?
解：直接暴力就好，
答案：563

试题 B: 扩散
本题总分:5 分

【问题描述】
小蓝在一张无限大的特殊画布上作画。
这张画布可以看成一个方格图,每个格子可以用一个二维的整数坐标表示。
小蓝在画布上首先点了一下几个点:(0, 0), (2020, 11), (11, 14), (2000, 2000)。
只有这几个格子上有黑色,其它位置都是白色的。
每过一分钟,黑色就会扩散一点。具体的,如果一个格子里面是黑色,它就会扩散到上、下、左、右四个相邻的格子中,使得这四个格子也变成黑色(如果原来就是黑色,则还是黑色)。
请问,经过 2020 分钟后,画布上有多少个格子是黑色的。

解：BFS，把四个起始点放入queue队列中，然后每次出队列一个，把周围的四个格子变为黑色，标记分钟，直到2020停止

答案：20312088

#include
#include
#include
#include
#include
#include
#include
#include
#include
#define N 100000
#define INF 0x3f3f3f3f
#define ll long long
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
using namespace std;
bool a[8000][8000];
int cnt=2020;
int dir[4][2]={
     0,1,0,-1,1,0,-1,0};

struct node{
     
	int x,y,step;
};
queue<node>qu;
void bfs() 
{
     
	a[0+3000][0+3000]=1;
	a[2020+3000][11+3000]=1;
	a[11+3000][14+3000]=1;
	a[2000+3000][2000+3000]=1;
	qu.push(node{
     0+3000,0+3000,0});
	qu.push(node{
     2020+3000,11+3000,0});
	qu.push(node{
     11+3000,14+3000,0});
	qu.push(node{
     2000+3000,2000+3000,0});
	while(qu.size())
	{
     
		node temp=qu.front();
		qu.pop();
		if(temp.step==cnt)
			continue;
		for(int i=0;i<4;i++)
		{
     
			int xx=temp.x+dir[i][0];
			int yy=temp.y+dir[i][1];
			if(!a[xx][yy])
			{
     
				a[xx][yy]=1;
				qu.push(node{
     xx,yy,temp.step+1});
			}
		}
	}
}
int main()
{
     
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int i,j;
	int sum=0;
	bfs();
	
	for(i=0;i<8000;i++)
	for(j=0;j<8000;j++)
	{
     
		sum+=a[i][j];
	}
	cout<<sum<<endl;
	return 0;
}

试题 C: 阶乘约数
本题总分:10 分

【问题描述】
定义阶乘 n! = 1 × 2 × 3 × · · · × n。
请问 100! （100 的阶乘）有多少个约数。

解：其实就是把从那些因子中挑出来问你最多能组成多少个数。
为了防止23=6的重复计算，我们不能直接挑，所以要先用唯一分解定理分解成素因子乘积的形式
如：5!=12345=2331*51;
所以现在的情况变成了：2有4种选择（0、1、2、3个），3有2种选择（0、1个），5有2种选择（0、1个）.即每个素因子的选择个数是其幂次+1。
所以对于100！的答案就是把2-100的每一个数进行分解，记录下每一个素因子的个数，然后+1乘起来即可

答案：39001250856960000

#include
#include
#include
using namespace std;

int main()
{
     
	int a[101];
	long long sum=1;
	memset(a,0,sizeof(a));
	for(int i=2;i<=100;i++)
	{
     
		int temp=i;
		for(int j=2;j<=temp;j++)
		{
     
			while(temp%j==0)
			{
     
				temp=temp/j;
				a[j]++;
			}
		}
	}
	for(int i=2;i<=100;i++)
	{
     
		if(a[i]!=0)
		sum=sum*(a[i]+1);
	}
	cout<<sum<<endl;
}

试题 D: 本质上升序列
本题总分:10 分

【问题描述】
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt,内容与下面的文本相同)
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?

解：我们先考虑如果出现重复的字符串怎么办：比如axxbxxxb，那么有两个ab递增子序列，则对于该ab递增子序列，在其后面延展字母构成新的递增子序列个数我们可以发现肯定是前一个ab的递增子序列的个数要>=第二个的，可以说第二个的答案是第一个是子集。那么我们对于同一种的递增子序列我们只需要记录其最早出现的即可，后续的出现也不需要管了。
基于上述所讲，我们可以使用BFS，使用队列，队列内记录字符串以及该递增子序列最后一个字符的位置，对于每次队首的字符串s，其末尾位置设为t，我们只需要从t+1到s.size()-1位置找到任何比s[t]大的即可插入到队列中去，这个过程进行去重、计数即可。
答案：3616159

#include
#include
#include
#include
#include
using namespace std;
map<string,int>mp;

int main()
{
     
	string str;
	int ans=0;
	cin>>str;
	queue<pair<string,int> >qu;
	for(int i=0;i<=str.size()-1;i++)
	{
     
		string s="";
		s=s+str[i];
		if(!mp[s])
		{
     
			mp[s]++;
			qu.push(make_pair(s,i));
			ans++;
		}
	}
	while(qu.size())
	{
     
		string st=qu.front().first;
		int ii=qu.front().second;
		qu.pop();
		for(int i=ii+1;i<=str.size()-1;i++)
		{
     
			if(str[i]>str[ii]&&!mp[st+str[i]])
			{
     
				mp[st+str[i]]=1;
				qu.push(make_pair(st+str[i],i));
				ans++;
			}
		}
	}
	cout<<ans<<endl;
}

试题 E: 玩具蛇
本题总分:15 分

【问题描述】
小蓝有一条玩具蛇,一共有 16 节,上面标着数字 1 至 16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4 的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母 A 到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:

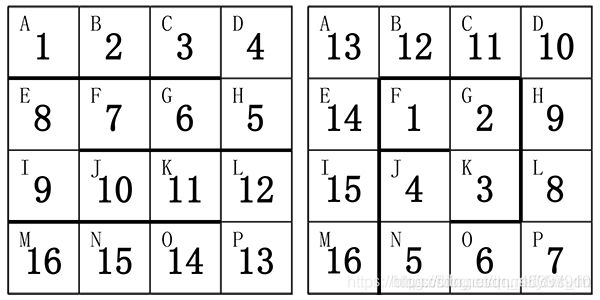
解：同样是BFS，从每一个格子开始，暴力就好
答案：552

#include
#include
using namespace std;
long long  ans;
int dir[4][2]={
      {
     0,1},{
     1,0},{
     0,-1},{
     -1,0} };
int vis[4][4];
void dfs(int x,int y,int cnt)
{
     
	if(x>=4||y>=4||x<0||y<0)
	return ;
	if(cnt==16)
	{
     
		ans++;
	}
	for(int i=0;i<4;i++)
	{
     
		int xx=x+dir[i][0];
		int yy=y+dir[i][1];
		if(vis[xx][yy])
			continue;
		
		vis[xx][yy]=1;
		dfs(xx,yy,cnt+1); 
		vis[xx][yy]=0;
	}
	
}
int main()
{
     
	for(int i=0;i<4;i++)
	for(int j=0;j<4;j++)
	{
     
		memset(vis,0,sizeof(vis));
		vis[i][j]=1;
		dfs(i,j,1);
		vis[i][j]=0;
	}
	cout<<ans<<endl;
}