C++进阶数据结构_红黑树

1. R-B Tree简介

• R-B Tree，全称是Red-Black Tree，又称为“红黑树”，它一种特殊的二叉搜索树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

1.1 红黑树的特性

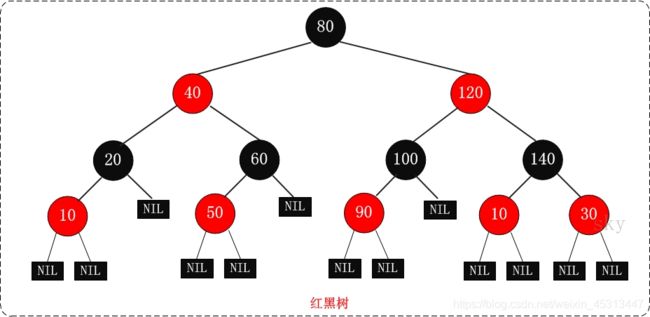
1. 每个节点或者是黑色，或者是红色。
2. 根节点是黑色。
3. 每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
4. 如果一个节点是红色的，则它的子节点必须是黑色的。
5. 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

注意：

1. 特性3中的叶子节点，是只为空的节点。
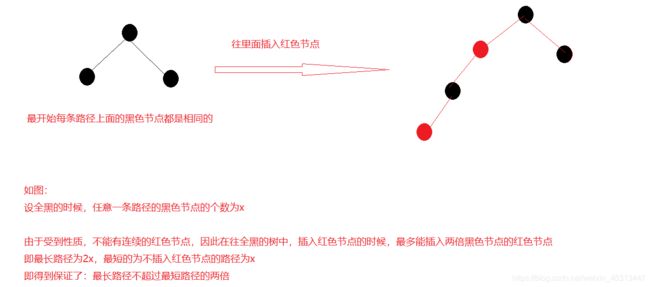
2. 特性5确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。

1.2 红黑树示意图

2 性质分析

2.1 与AVL树进行比较

• 设红黑树的黑色节点数为x个，任意一颗红黑树中，总结点的个数N为[x,2x]，即查找的效率为 logN~log2N 即O(logN)。
  底层实现中，AVL是严格的平衡二叉树，红黑树只是近似平衡二叉树，即AVL树要进行更多的旋转操作，因此红黑树的性能更优于AVL树。常用的set和map在底层用的就是红黑树。

3. 红黑树的基本操作

• 红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后，都会用到旋转方法。为什么呢？添加或删除红黑树中的节点之后，红黑树就发生了变化，可能不满足红黑树的5条性质，也就不再是一颗红黑树了，而是一颗普通的树。而通过旋转，可以使这颗树重新成为红黑树。简单点说，旋转的目的是让树保持红黑树的特性。
  旋转包括两种：左旋 和 右旋。下面分别对它们进行介绍：

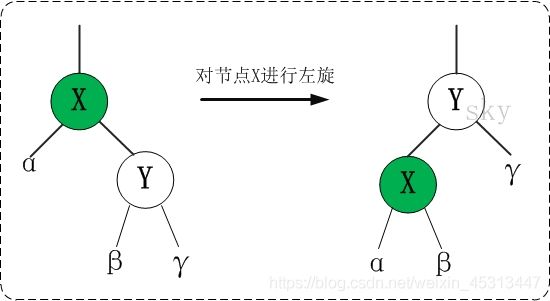
3.1 左旋

• 对x进行左旋，意味着"将x变成一个左节点"。
  

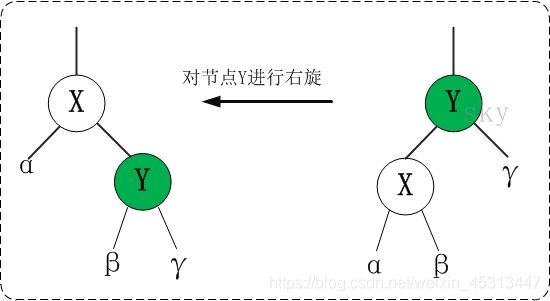
3.2 右旋

• 对Y进行右旋，意味着"将Y变成一个右节点"。
  

3.3 添加

• 将一个节点插入到红黑树中，需要执行哪些步骤呢？首先，将红黑树当作一颗二叉查找树，将节点插入；插入的结点为红色；最后，通过旋转和重新着色等方法来修正该树，使之重新成为一颗红黑树。详细描述如下：

第一步: 将红黑树当作一颗二叉查找树，将节点插入。

• 红黑树本身就是一颗二叉查找树，将节点插入后，该树仍然是一颗二叉查找树。也就意味着，树的键值仍然是有序的。此外，无论是左旋还是右旋，若旋转之前这棵树是二叉查找树，旋转之后它一定还是二叉查找树。这也就意味着，任何的旋转和重新着色操作，都不会改变它仍然是一颗二叉查找树的事实。
  想方设法的旋转以及重新着色，使这颗树重新成为红黑树！

第二步：将插入的节点着色为"红色"。

• 为什么着色成红色，而不是黑色呢？为什么呢？在回答之前，我们需要重新温习一下红黑树的特性：
  (1) 每个节点或者是黑色，或者是红色。
  (2) 根节点是黑色。
  (3) 每个叶子节点是黑色。 [注意：这里叶子节点，是指为空的叶子节点！]
  (4) 如果一个节点是红色的，则它的子节点必须是黑色的。
  (5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
  将插入的节点着色为红色，不会违背"特性(5)"！少违背一条特性，就意味着我们需要处理的情况越少。接下来，就要努力的让这棵树满足其它性质即可；满足了的话，它就又是一颗红黑树了。

第三步: 通过一系列的旋转或着色等操作，使之重新成为一颗红黑树。

• 第二步中，将插入节点着色为"红色"之后，不会违背"特性(5)"。那它到底会违背哪些特性呢？
  对于特性(1)，显然不会违背了。因为我们已经将它涂成红色了。
  对于特性(2)，显然也不会违背。在第一步中，我们是将红黑树当作二叉查找树，然后执行的插入操作。而根据二叉查找数的特点，插入操作不会改变根节点。所以，根节点仍然是黑色。
  对于特性(3)，显然不会违背了。这里的叶子节点是指的空叶子节点，插入非空节点并不会对它们造成影响。
  对于特性(4)，是有可能违背的！
  那接下来，想办法使之满足特性(4)，就可以将树重新构造成红黑树了。

3.3.1父亲结点为黑色

• 父亲节点为黑色，插入的节点为红色，不需要进行操作。

3.3.2父亲节点为红色，叔叔节点存在，并且为红色

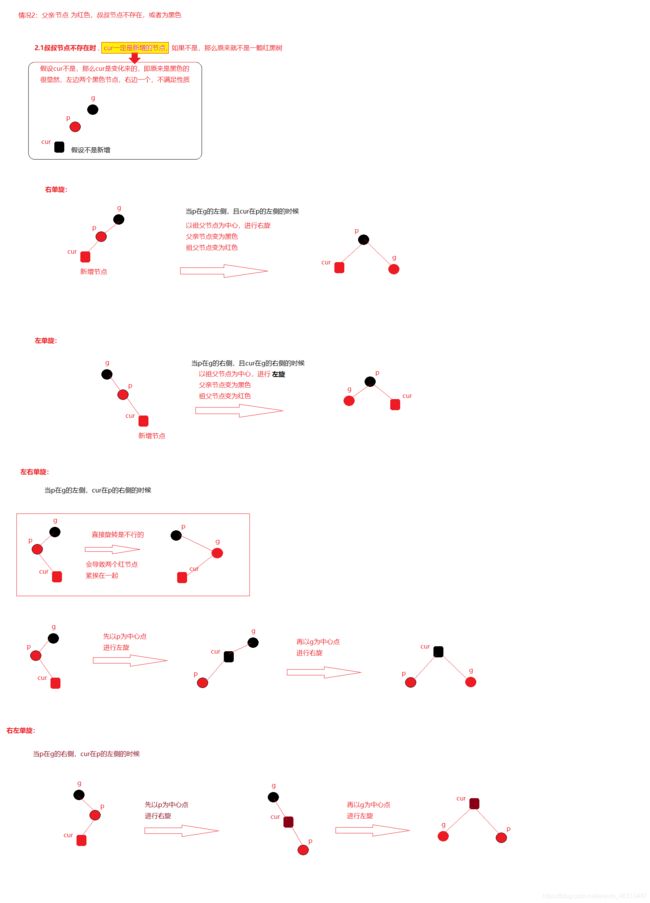
3.3.3父亲节点为红色，叔叔节点不存在或存在且为黑色

• 叔叔节点不存在
  
• 叔叔节点存在，且为黑色

4. 总结

红黑树的添加操作主要有以下几种：

1. 父亲节点是·黑色，插入的节点为红色，不需要进行操作。
2. 父亲节点和叔叔节点是红色，插入一个红色的节点后，父亲节点和叔叔节点变为黑色，祖父节点变为红色
3. 父亲节点是红色、叔叔节点不存在或者存在且为黑色：
   • parent在grandfather左侧：
     cur在parent左侧 -> 以祖父为中心，进行右旋，并且祖父变为红色，父亲变为黑色 (右旋)
     cur在parent右侧 -> 先以父亲为中心进行左旋，再以祖父为中心进行右旋 (左右双旋)
   • parent在grandfather右侧：
     cur在parent右侧 -> 以祖父为中心，进行左旋,并且祖父变为红色，父亲变为黑色 (左旋)
     cur在parent左侧 -> 先以父亲为中心进行右旋，再以祖父为中心进行左旋 (右左双旋)

5. 代码实现

#pragma once
#include 
using namespace std;

enum Color
{
     
	RED,
	BLACK
};


template<class K,class V>
struct RBTreeNode
{
     
	RBTreeNode(const pair<K, V>&kv)
	:_left(nullptr)
	, _right(nullptr)
	, _parent(nullptr)
	, _kv(kv)
	, _col(RED)
	{
     }

	RBTreeNode<K, V> *_left;
	RBTreeNode<K, V> *_right;
	RBTreeNode<K, V> *_parent;
	pair<K, V> _kv;
	enum  Color _col;
};

template<class K,class V>
class RBTree
{
     
	typedef RBTreeNode<K,V> Node;

public:

	void RotateL(Node *parent)//左旋
	{
     
		Node *subR = parent->_right;//左旋,p的右边一定不为空
		Node *subL = subR->_left;//可能为空
		Node *pparent = parent->_parent;

		//将subR左侧节点链接到p的右侧
		parent->_right = subL;
		if (subL != nullptr)
			subL->_parent = parent;

		//将p链接到subR的左侧
		subR->_left = parent;
		parent->_parent = subR;
		
		//subR与pp的链接
		subR->_parent = pparent;
		if (pparent == nullptr)
			_root = subR;
		else
		{
     
			if (pparent->_left == parent)
				pparent->_left = subR;
			else
				pparent->_right = subR;
		}

		//颜色更改
		parent->_col = RED;
		subR->_col = BLACK;

	}

	void RotateR(Node *parent)//右旋
	{
     
		Node *subL = parent->_left;
		Node *subR = subL->_right;
		Node *pparent = parent->_parent;

		parent->_left = subR;
		if (subR != nullptr)
			subR->_parent = parent;

		subL->_right = parent;
		parent->_parent = subL;

		subL->_parent = pparent;
		if (pparent == nullptr)
			_root = subL;
		else
		{
     
			if (pparent->_left == parent)
				pparent->_left = subL;
			else
				pparent->_right = subL;
		}

		//颜色更改
		parent->_col = RED;
		subL->_col = BLACK;

	}

	pair<Node*, bool> Insert(pair<K, V>&kv)
	{
     
		if (_root == nullptr)
		{
     
			_root = new Node(kv);
			_root->_col = BLACK;
			return make_pair(_root, true);
		}

		//有根节点了
			Node *parent = nullptr;
			Node *cur = _root;

			while (cur)
			{
     
				if (kv.first > cur->_kv.first)
				{
     
					parent = cur;
					cur = cur->_right;
				}
				else if (kv.first < cur->_kv.first)
				{
     
					parent = cur;
					cur = cur->_left;
				}
				else//相等，，去重
				{
     
					return make_pair(cur, false);
				}

			}

			//此时进行节点的插入
			cur = new Node(kv);
			Node* newnode = cur;//保存一份，返回用

			if (parent->_kv.first > kv.first)//在左边
			{
     
				parent->_left = cur;
				cur->_parent = parent;
			}
			else//在右边
			{
     
				parent->_right = cur;
				cur->_parent = parent;
			}

			//插入红色的节点，维护规则-》相邻节点不能同样是红色

			while (parent&&parent->_col == RED)//父亲节点不为空，并且为红色，说明此时需要进行调整
			{
     
				Node *grandfather = parent->_parent;//父亲节点存在且为红色，那么一定不是根节点

					Node *uncle = grandfather->_right;
					if (grandfather->_right == parent)//父亲节点为右，则叔叔节点为左
						uncle = grandfather->_left;

					if (uncle != nullptr&&uncle->_col == RED)//情况1：叔叔节点存在且为红色
					{
     
						//颜色更改
						parent->_col = BLACK;
						uncle->_col = BLACK;
						grandfather->_col = RED;

						//继续向上判断
						cur = grandfather;//新的红节点
						parent = cur->_parent;//
					}
					else//叔叔节点不存在，或者存在为黑色
					{
     
						if (grandfather->_left == parent)//p在g的左侧
						{
     
							if (cur == parent->_left)//c在p的左侧，只需要进行右旋
							{
     
								RotateR(grandfather);
							}
							else//c在p的右侧，先左再右
							{
     
								RotateL(parent);
								RotateR(grandfather);
							}
						}
						else//p在g的右侧
						{
     
							if (cur == parent->_right)//c在p的右侧，左旋
							{
     
								RotateL(grandfather);
							}
							else//先右再左旋
							{
     
								RotateR(parent);
								RotateL(grandfather);
							}
						}
						break;//旋转之后即完成了要求，不需要再进行判断
					}
			}

		_root->_col = BLACK;//防止根节点被改成红色，根节点赋予黑色，每条路径上都是适用的
		return make_pair(newnode, true);
	}

	//[]重载

	V &operator [](const K &k)//string、int、vector等等都可以是V，是由默认的构造函数的 int()=0
	{
     
		//insert返回的是pair

		return  ((Insert(make_pair(k, V())).first)->_kv).second;
	}


	//检测相关

	//遍历
	void _Inorder(Node *root)
	{
     
		if (root == nullptr)
			return;
		_Inorder(root->_left);

		cout << root->_kv.first << " " << root->_kv.second <<" "<<root->_col<< endl;
		_Inorder(root->_right);

	}

	void Inorder()
	{
     
		_Inorder(_root);
	}



	//判断是否是红黑树 ->判断一个红色节点的左右子树是否是红色的  -> 判断一个红色节点的父亲是否是红色的

	bool CheckCol(Node* root)
	{
     
		if (root == nullptr)
			return true;

		if (root->_col == RED)//当前节点为红色
		{
     
			if (root->_parent != nullptr)
			{
     
				if (root->_parent->_col == RED)//红色节点的父亲也为红色，则不是红黑树
				{
     
					cout << root->_kv.first << " " << root->_kv.second <<"颜色判断失败 ->不是红黑树"<< endl;
					return false;
				}
			}
		}

		return CheckCol(root->_left) && CheckCol(root->_right);
	}

	bool CheckBlack(Node *root,int TrueNum,int BlackNum)//统计路径上面的黑色节点
	{
     
		if (root == nullptr)//表示一条路径走到底了
		{
     
			return TrueNum == BlackNum;//判断每条路径的黑色节点是否相等
		}
		
		
		if (root->_col == BLACK)
			BlackNum++;

		return
			CheckBlack(root->_left, TrueNum, BlackNum) &&
			CheckBlack(root->_right, TrueNum, BlackNum);
	}


	bool Check()
	{
     
		Node *cur = _root;
		int TrueNum = 0;
		
		if (_root&&_root->_col == RED)//根不能为红色
		{
     
			return false;
		}

		while (cur)//统计一条路径上面的黑色节点的个数
		{
     
			if (cur->_col == BLACK)
				TrueNum++;
			cur = cur->_left;
		}


		return CheckCol(_root) && CheckBlack(_root, TrueNum, 0);

	}
	
private:
	Node *_root = nullptr;

};