树状数组从前往后求和,用来解第k大(或小)的数 poj 2985 The k-th Largest Group
来自http://www.cnblogs.com/oa414/archive/2011/07/21/2113234.html的启发,
看上述博客如何求第k大的数时,被其第二份代码影响,感觉很巧妙,于是研究了一下,搞懂后顿时神清气爽啊。。。
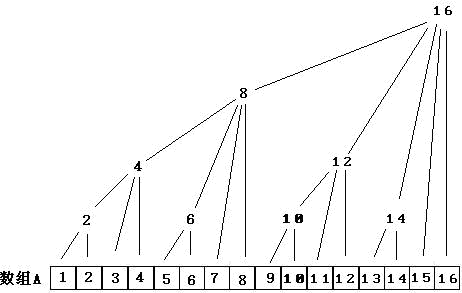
还是看这张经典的图吧,知识在图上就变得形象多了
现在假设要求sum[a]的值,一般我们都是从后往前求和,如a=15
15-lowbit(15)=14;
14-lowbit(14)=12;
12-lowbit(12)=8;
8-lowbit(b)=0;
答案就是sum[15]+sum[14]+sum[12]+sum[8];
现在我们可以这样来求,从不超过15的只有一个1的最大二进制数开始,也可以理解为指数从log(15)取整开始,即3,2的3次等于8,依次加上2的2次,2的1次,2的0次,数字依次为8,12,14,15,也就是把普通的求和过程反向。
好了,方向求和有什么好处呢?
在求第k大的数的时候就派上用场了,虽然还有很多其他方法可以解决第k大的数,但树状数组无疑是最优雅的方法了
下面就以poj 2418这一题来简单说一下怎么求第k大的数
由于树状数组记录的是比当前元素小的数的个数,所以可以先把求第k大的数转换为求第num-k+1小的数,num是总的数的个数
int find_kth(int k)//太神奇了(大概是以前没有完全领会),log(n)复杂度
{
int ans = 0, cnt = 0, i;
for (i = 20; i >= 0; i--)//利用二进制的思想,把答案用一个二进制数来表示
{
ans += (1 << i);
if (ans >= maxn|| cnt + c[ans] >= k)
//这里大于等于k的原因是可能会有很多个数都满足cnt + c[ans] >= k,所以找的是最大的满足cnt+c[ans]<k的ans
ans -= (1 << i);
else
cnt += c[ans];//cnt用来累加比当前ans小的总组数
}//求出的ans是累加和(即小于等于ans的数的个数)小于k的情况下ans的最大值,所以ans+1就是第k大的数
return ans + 1;
}
完整代码即详细注释
 View Code
View Code
#include<stdio.h>
#include<string.h>
#define maxn 300000
int a[maxn],c[maxn],p[maxn];//值为i的数有i个
int find(int x){return x==p[x] ? x : p[x]=find(p[x]);}
int lowbit(int x){
return x&-x;
}
void update(int x,int d){
for(;x<=maxn;x+=lowbit(x))
c[x]+=d;
}//因为是从左往右手动求和了,所以也不需要sum()操作了
int find_kth(int k)//太神奇了(大概是以前没有完全领会),log(n)复杂度
{
int ans = 0, cnt = 0, i;
for (i = 20; i >= 0; i--)//利用二进制的思想,把答案用一个二进制数来表示
{
ans += (1 << i);
if (ans >= maxn|| cnt + c[ans] >= k)
//这里大于等于k的原因是可能大小为ans的数不在c[ans]的控制范围之内,所以这里求的是 < k
ans -= (1 << i);
else
cnt += c[ans];//cnt用来累加比当前ans小的总组数
}//求出的ans是累加和(即小于等于ans的数的个数)小于k的情况下ans的最大值,所以ans+1就是第k大的数
return ans + 1;
}
/*
因为要求第k小的数,所以要从左往右加过去,
上述过程其实就是把树状数组的求和操作逆向,从左往右求和,
边求和边判断控制范围内比当前值要小的数是否超过或等于k,如果是则跳回兄弟节点(ans-=(1<<i))
如8+4=12,假如12不满足要求,则重新变回8,下一次就加2,8+2=10,即跳到10控制的位置
上述累加过程不会重复计算,因为
比如15=8+4+2+1,数字依次为8 12 14 15,每次累加后的值都与前面的值无关,i小于其二进制末尾0的个数
即c[8] 、c[12] 、c[14]、 c[15]相加的话不会重复计算,再如11=8+2+1;数字依次为8 10 11,c[8],c[10],c[11]
各自控制着自己的范围,不会重复累加,所以就可以用cnt来累加前面的结果,最后cnt+c[ans]就表示了值<=ans的个数
简言之:上述的各个数字两两间控制的范围不会相交
*/
int main()
{
int i,n,m,q,x,y,k,l,r;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++) p[i]=i;
for(i=1;i<=n;i++) a[i]=1;
update(1,n);//初始状态值为1的数有n个
int num=n;
for(i=1;i<=m;i++)
{
scanf("%d",&q);
if(q==0)
{
scanf("%d%d",&x,&y);
x=find(x);
y=find(y);
if(x==y) continue;
update(a[x],-1);
update(a[y],-1);
update(a[x]+a[y],1);
p[y]=x;
a[x]+=a[y];
num--;//合并集合
}
else
{
scanf("%d",&k);
k=num-k+1;//转换为找第k小的数
printf("%d\n",find_kth(k));
}
}
return 0;
}
二分做法
 View Code
View Code
#include<stdio.h>
#include<string.h>
#define maxn 300000
int a[maxn],c[maxn],p[maxn];//值为i的数有i个
int find(int x){return x==p[x] ? x : p[x]=find(p[x]);}
int lowbit(int x){
return x&-x;
}
void update(int x,int d){
for(;x<=maxn;x+=lowbit(x))
c[x]+=d;
}
int sum(int x){
int ans=0;
for(;x>0;x-=lowbit(x))
ans+=c[x];
return ans;
}
int main()
{
int i,n,m,q,x,y,k,l,r;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++) p[i]=i;
for(i=1;i<=n;i++) a[i]=1;
update(1,n);//初始状态值为1的数有n个
int num=n;
for(i=1;i<=m;i++)
{
scanf("%d",&q);
if(q==0)
{
scanf("%d%d",&x,&y);
x=find(x);
y=find(y);
if(x==y) continue;
update(a[x],-1);
update(a[y],-1);
update(a[x]+a[y],1);
p[y]=x;
a[x]+=a[y];
num--;//合并集合
}
else
{
scanf("%d",&k);
k=num-k+1;//转换为找第k小的数
l=1;
r=n;
while(l <= r)
{
int mid=(l+r)>>1;
if(sum(mid) >= k) r=mid-1;//尽量往左逼近
else l=mid+1;
}
printf("%d\n",l);
}
}
return 0;
}
好像还可以用平衡树,线段树等来做,改天再补上
treap写法:比树状数组还快
 View Code
View Code
#include<cstdio> #include<set> #include<cstdlib> #include<cstring> using namespace std; const int maxn = 300010; #define L ch[rt][0] #define R ch[rt][1] int ch[maxn][2], aux[maxn] , num[maxn] , size[maxn] , cnt[maxn]; int val[maxn]; int tot,rt; inline void init(){ size[0]=0; rt = tot = 0; ch[0][0] = ch[0][1] = 0; aux[0] = 0; } inline void pushup(int rt){ size[rt]=cnt[rt]+size[L]+size[R]; } inline void Rotate(int &rt,int f){//f=1:右旋 f=0:左旋 int t = ch[rt][!f]; ch[rt][!f] = ch[t][f]; ch[t][f] = rt; pushup(rt);pushup(t); rt = t; } void insert(int &rt,int key){ if(!rt) { rt = ++tot; val[rt] = key; L = R = 0; size[rt]=cnt[rt]=1; aux[rt] = ( rand() << 14 ) + rand(); return ; } if(key==val[rt]) { ++cnt[rt]; }else if(key < val[rt]){ insert(L , key); if( aux[L] < aux[rt] ) Rotate(rt,1); }else { insert(R , key); if( aux[R] < aux[rt] ) Rotate(rt,0); } pushup(rt); } void treap_delete(int &rt){//real deletion if(!L || !R){ rt=L?L:R; }else { if(aux[L] < aux[R]){ Rotate(rt,1); treap_delete(R); }else { Rotate(rt,0); treap_delete(L); } } } void del(int &rt , int key){//lazy deletion if(key == val[rt]) { cnt[rt]--; size[rt]--; if(cnt[rt]==0) treap_delete(rt); } else { if(key < val[rt]) del(L,key); else del(R,key); size[rt]--; } } int find(int rt,int key){ if(!rt) return 0; else if(key < val[rt]) return find(L,key); else if(key > val[rt]) return find(R,key); else return cnt[rt]; } //找后继结点 void succ(int rt,int key,int &ans){//找>=key的第一个结点,即后继结点 if(!rt) return ; if(val[rt] >= key){ ans=val[rt]; succ(L,key,ans); }else succ(R,key,ans); } //找前驱结点 void pre(int rt,int key,int &ans){ if(!rt) return ; if(val[rt]<=key) { ans=val[rt]; succ(R,key,ans); }else succ(L,key,ans); } int getmin(int rt){ while(L) rt=L; return val[rt]; } int getmax(int rt){ while(R) rt=R; return val[rt]; } //找第k小的数 int find_kth(int rt,int k){ if(k<size[L]+1) return find_kth(L,k); else if(k>size[L]+cnt[rt]) return find_kth(R,k-size[L]-cnt[rt]); else return val[rt]; } //确定key的排名 int treap_rank(int rt,int key,int cur){//cur:当前已知比要求元素(key)小的数的个数 if(key == val[rt]) return size[L] + cur + 1; else if(key < val[rt]) treap_rank(L,key,cur); else treap_rank(R,key,cur+size[L]+cnt[rt]); } int a[maxn],c[maxn],p[maxn];//值为i的数有i个 int find(int x){return x==p[x] ? x : p[x]=find(p[x]);} int main() { init(); int i,n,m,q,x,y,k,l,r; scanf("%d%d",&n,&m); for(i=1;i<=n;i++) p[i]=i; for(i=1;i<=n;i++) a[i]=1; for(int i=1;i<=n;i++) insert(rt,1); int num=n; for(i=1;i<=m;i++) { scanf("%d",&q); if(q==0) { scanf("%d%d",&x,&y); x=find(x); y=find(y); if(x==y) continue; del(rt,a[x]); del(rt,a[y]); insert(rt,a[x]+a[y]); p[y]=x; a[x]+=a[y]; num--;//合并集合 } else { scanf("%d",&k); k=num-k+1;//转换为找第k小的数 printf("%d\n",find_kth(rt,k)); } } return 0; }
