Bitmap - 性能和原理研究

注：本文转自我的个人博客（Bitmap - 性能和原理研究）

Paper原文地址：An Experimental Study of Bitmap Compression vs.
Inverted List Compression
Bitmap可以说是一个很万能的存储了，无论是空间消耗，还是查询响应，在最佳实践下，都可以达到很好的效果。最近做了不少Bitmap的研究，简单的基于上面的Paper去做一个记录。

---

History

从最原始的Bitmap到RoaringBitmap（可能是目前大多数场景的最佳选择？），虽然仔细研究Roaring的原理并不复杂，但也是经过了十几年的变化和迭代。

WAH(Word Aligned Hybrid)

这个算法只压缩全0或者全1的group。将所有bits按照连续的31bit进行分组，然后对每一组进行编码，编码后的长度为32bit。具体结构如下图所示：

WAH

EWAH(Enhanced Word Aligned Hybrid)

基于WAH加了一个Header，作为元信息的存储。我理解这其实并没有在存储上做到太多帮助的优化，反而是在查询或者插入中，会更加便捷。Header结构如下所示。

EWAH

CONCISE(Compressed N Composble Integer Set)

这也是基于WAH做的一个优化。在WAH算法中，只要有一个bit被置1，那么整个group都无法被压缩，这一算法在这种odd bit上做了优化。记录了这个单一odd bit的位置。

CONCISE

VALWAH(Variable-Aligned Length WAH)

基于参数的优化，缓解了WAH的每个group固定32bit的限制（因为32bit最多能表示2^31 - 1个压缩group，但是实际上不会那么多）。采用了参数去调控，没有固定的规则，对于不同的bitmap自动采用不同的参数，很影响查询的效率。

Roaring

以65535bit分bucket，每个bucket里的integer共享高16bit（为bucket的编号），例如第一个bucket为[0 ~ 65535]，高16bit为0，第二个bucket为[65536 ~ 65536*2 - 1]，高16bit为1。其中，65536中以short integer(16bit)为单位表示integer的低16bit。所以当这个bucket中integer 个数 > 4096时，不存在压缩。

---

RoaringBitmap源码解读

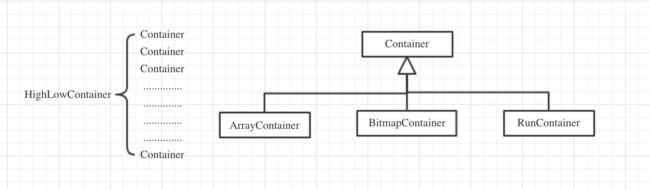
RoaringBitmap的基本构成如下:HighLowContainer中存储了每个Integer的高16bit的公共索引keys以及具体存储数字的Container。由于Container是最终的载体，所以优化基本都在Container里。下面直接分析源码中的Add方法，通过这个方法基本上可以看出Container的内部结构。

RoaringBasic

先看一个代码里比较常出现的binarySearch方法，这里比较灵活的一点是，如果找到则返回对应的index，如果没找到则返回对应位置的负数，这样既可以传递位置信息，又可以传递是否存在的信息。

protected static int hybridUnsignedBinarySearch(final short[] array, final int begin,
      final int end, final short k) {
    int ikey = toIntUnsigned(k);
    // next line accelerates the possibly common case where the value would
    // be inserted at the end
    if ((end > 0) && (toIntUnsigned(array[end - 1]) < ikey)) {
      return -end - 1;
    }
    int low = begin;
    int high = end - 1;
    // 32 in the next line matches the size of a cache line
    while (low + 32 <= high) {
      final int middleIndex = (low + high) >>> 1;
      final int middleValue = toIntUnsigned(array[middleIndex]);

      if (middleValue < ikey) {
        low = middleIndex + 1;
      } else if (middleValue > ikey) {
        high = middleIndex - 1;
      } else {
        return middleIndex;
      }
    }
    // we finish the job with a sequential search
    int x = low;
    for (; x <= high; ++x) {
      final int val = toIntUnsigned(array[x]);
      if (val >= ikey) {
        if (val == ikey) {
          return x;
        }
        break;
      }
    }
    return -(x + 1);
}

ArrayContainer

short[] content;

@Override
public Container add(final short x) {
    int loc = Util.unsignedBinarySearch(content, 0, cardinality, x);
    if (loc < 0) {
      // Transform the ArrayContainer to a BitmapContainer
      // when cardinality = DEFAULT_MAX_SIZE
      if (cardinality >= DEFAULT_MAX_SIZE) {
        BitmapContainer a = this.toBitmapContainer();
        a.add(x);
        return a;
      }
      if (cardinality >= this.content.length) {
        increaseCapacity();
      }
      // insertion : shift the elements > x by one position to
      // the right
      // and put x in it's appropriate place
      System.arraycopy(content, -loc - 1, content, -loc, cardinality + loc + 1);
      content[-loc - 1] = x;
      ++cardinality;
    }
    return this;
}

相关变量说明：

• content: 为了增删改查的方便性，采用short有序数组来存储数字(注意高16bit已经存储在HighLowContainer中，所以这里只需要存储低16bit的short就满足了)。
• DEFAULT_MAX_SIZE: 由于有序数组在插入时需要做二分查找，效率较低，所以这里有一个限定4096，超过这个大小自动转成BitmapContainer。

add流程如下：

1. 通过二分查找找到x所在的content中的位置，若存在则不处理，不存在则进入下一步。
2. 对cardinality进行判断，决定是否需要升级Container或者扩容。
3. 将content中loc之后的子数组后移一位，将数据插入，形成新的content数组。

BitmapContainer

final long[] bitmap;

@Override
public Container add(final short i) {
    final int x = Util.toIntUnsigned(i);
    final long previous = bitmap[x / 64];
    long newval = previous | (1L << x);
    bitmap[x / 64] = newval;
    if (USE_BRANCHLESS) {
      cardinality += (previous ^ newval) >>> x;
    } else if (previous != newval) {
      ++cardinality;
    }
    return this;
}

相关变量说明：

• bitmap: 1个Container中可以存储65536(2^16 bit)个数字Integer，在BitmapContainer中再以long(2^6bit)做分组，形成了long数组。

add流程如下:

1. 通过x/64找到bitmap中的long数组中的位置得到原值previous。
2. previous | (1L << x) 得到newval。
3. 改变cardinality。
   可以发现当Integer分布稠密时，容易在一个long中出现连续1的情况，在这种情况下也存在优化空间，可以调用runOptimize升级为RunContainer。

RunContainer

主要解决了连续1的情况，例如15、16、17、18可以被优化成15,3。RunContainer中的关键变量为valuesLength，类型是short[]。其中，2n位是具体数值，2n+1为2n往后的连续个数。
例如：valuesLength = [1,3,15,2,88,4]表达的RoaringBitmap为1,2,3,15,16,88,89,90,91。

private short[] valueslength;
int nbrruns = 0;

add方法如下所示:

@Override
public Container add(short k) {
    // TODO: it might be better and simpler to do return
    // toBitmapOrArrayContainer(getCardinality()).add(k)
    // but note that some unit tests use this method to build up test runcontainers without calling
    // runOptimize
    int index = unsignedInterleavedBinarySearch(valueslength, 0, nbrruns, k);
    if (index >= 0) {
      return this;// already there
    }
    index = -index - 2;// points to preceding value, possibly -1
    if (index >= 0)   {// possible match
      int offset = toIntUnsigned(k) - toIntUnsigned(getValue(index));
      int le = toIntUnsigned(getLength(index));
      if (offset <= le) {
        return this;
      }
      if (offset == le + 1) {
        // we may need to fuse
        if (index + 1 < nbrruns) {
          if (toIntUnsigned(getValue(index + 1)) == toIntUnsigned(k) + 1) {
            // indeed fusion is needed
            setLength(index,
                (short) (getValue(index + 1) + getLength(index + 1) - getValue(index)));
            recoverRoomAtIndex(index + 1);
            return this;
          }
        }
        incrementLength(index);
        return this;
      }
      if (index + 1 < nbrruns) {
        // we may need to fuse
        if (toIntUnsigned(getValue(index + 1)) == toIntUnsigned(k) + 1) {
          // indeed fusion is needed
          setValue(index + 1, k);
          setLength(index + 1, (short) (getLength(index + 1) + 1));
          return this;
        }
      }
    }
    if (index == -1) {
      // we may need to extend the first run
      if (0 < nbrruns) {
        if (getValue(0) == k + 1) {
          incrementLength(0);
          decrementValue(0);
          return this;
        }
      }
    }
    makeRoomAtIndex(index + 1);
    setValue(index + 1, k);
    setLength(index + 1, (short) 0);
    return this;
}

这里的决策方法略为复杂，用流程图来表示应该会比较直观。

FLOW

Container之间比较如下：

Container	空间利用率	查询效率
ArrayContainer	无压缩、低	使用二分查找，低
BitmapContainer	无压缩、低	直接利用索引命中，高
RunContainer	有压缩、高	顺序查找，中