堆和堆排序

1. 堆的基础知识

1.1 什么是堆

堆是一种特殊的二叉树，它需要满足如下两个条件

堆是一颗完全二叉树
堆中每个节点的值都大于或等于（小于或等于）它的子节点的值

我们把每个节点都大于或等于它的子节点的值的对叫做大顶堆；每个节点的值都小于等于它的子节点的堆叫做小顶堆。

上面图中这几颗树，第1个和第2个是大顶堆，第3个是小顶堆，第4个不是堆，它不是一颗完全二叉树

1.2 堆的存储

根据堆是一颗完全二叉树的特性，所以我们可以使用数组来存储堆。

假如我们从数组的下标1开始存储，则如图的这样一个堆对应的存储如图中数组

从数组下标为1的位置开始存储，完全二叉树的节点关系

下标为i的节点的左孩子的下标就是i*2
下标为i的节点的右孩子的下标就是i*2+1

根据完全二叉树的特性，最后一个非叶子节点是第n/2个节点，这里从数组下标1开始存储，所以最后一个非叶子节点对应的下标就是n/2。第1到第n/2个节点是非叶子结点，第n/2+1到第n个节点是叶子结点。

1.3 堆的常见操作

堆中常见的操作有:插入一个元素、删除堆顶元素

1.3.1 插入一个元素

插入一个元素可以将要插入的元素放到堆的最后面，然后对这个元素采用自下而上的方式来进行堆化

将插入的元素放到堆的最后的示意图

插入一个元素的堆化过程就是沿着节点所在的路径，自下而上和父节点比较大小，如果父子节点之间不满足大小关系，则交换两个节点的位置，然后继续拿着插入节点和新的父节点比较，直到满足大小关系或者插入节点已经是堆顶元素了

插入元素的堆化过程示意图

1.3.2 删除堆顶元素

删除堆顶元素，我们采用使用堆中最后一个元素来替代堆顶元素，然后对新的堆顶元素自顶向下的堆化的方式来实现

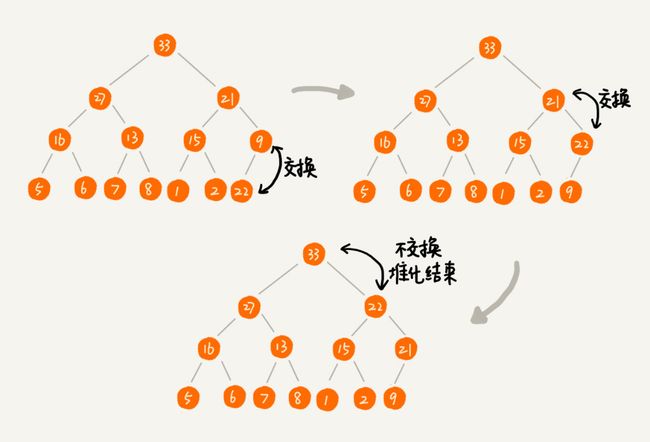
删除堆顶元素的过程（我们以维护一个大顶堆来讲解）：第一步，拿堆中最后一个元素替换掉堆顶元素；第二步：比较新的堆顶元素和它的左右孩子中值较大的孩子之间的大小，如果不满足大小关系，则交换堆顶元素与值较大的孩子之间的位置，然后拿着刚才那个堆顶元素和它新的左右孩子中的值较大的孩子比较，重复这个过程，直到满足大小关系或者新的堆顶元素已经交换到了叶子节点的位置

删除堆顶元素的堆化过程示意图

1.4 如何创建一个堆

创建一个堆有两种思路

第一种是借助前面讲的，在堆中插入一个元素的思路。我们假设起始堆中只包含一个数据，就是下标为1的数据，然后我们调用前面讲的插入操作，将下标为2到n的数据依次插入到堆中。这样我们就将包含n个数据的数组，组织成了堆。
第二种实现思路，跟第一种截然相反。第一种建堆思路的处理过程是从前往后处理数据，并且每个数据插入堆中时，都是从下往上堆化。第二种实现思路，是从后往前处理数据，并且每个数据都是从上往下堆化。具体实现就是从最后一个非叶子节点开始，依次堆化每个非叶子节点，每个节点都从上往下完成堆化

下面我们看一个堆化过程演示，我们依次对8,19,5,7四个非叶子节点进行了从上到下的堆化

堆化过程示意图

代码实现

public static void createHeap(int[] a, int n) {
    /**
     * 构建过程：从最后一个非叶子节点开始，从后往前，对每个节点进行自上而下的堆化
     */
    for (int i = n / 2; i >= 1; i--) {
        heapify(a, n, i);
    }
}

/**
 * 堆化根节点：找出当前节点的左右孩子中较大的一个，和根节点比较，符合顺序则结束；不符合顺序，则交换并继续比较
 *
 * @param a
 * @param n
 * @param i
 */
private static void heapify(int[] a, int n, int i) {
    int current = i;
    while (true) {
        int maxPos = -1;
        int left = current * 2;//左孩子的位置
        int right = left + 1;//右孩子的位置
        if (right <= n) {
            if (a[left] < a[right]) {
                maxPos = right;
            } else {
                maxPos = left;
            }
        } else if (left <= n) {
            maxPos = left;
        }
        if (maxPos == -1) {//没有子孩子
            break;
        }
        if (a[current] >= a[maxPos]) {//根节点比子孩子大
            break;
        } else {//和子孩子交换位置，继续比较
            int temp = a[maxPos];
            a[maxPos] = a[current];
            a[current] = temp;
            current = maxPos;
        }
    }
}

2. 堆的应用：堆排序

2.1 如何利用堆进行排序

假如我们要进行从小到大的排序，那我们先将数据建立一个大顶堆，这样建堆完成之后，数组中的数据就已经是按照大顶堆的特性来组织的了。数组中的第一个元素就是堆顶元素，也就是最大的元素。我们把它和最后一个元素交换，那最大元素就放到了下标为n的位置。

这个过程有点类似于“删除堆顶元素”的操作，当堆顶元素移除之后，我们把下标为n的元素放到堆顶，然后再通过堆化的方法，将剩下的n-1个元素重新构建成堆。堆化完成之后，我们再取堆顶元素和第n-1个元素交换位置，然后再将前面的n-2个元素堆化，一直重复这个过程，直到最后堆中只剩下下标为1的一个元素，排序工作就完成了。

排序过程演示图

代码实现

public static void sort(int[] a, int n) {
    //将堆顶元素和最后一个元素交互位置，然后自上而下堆化前面n-1个元素；重复这个过程直到堆中只有一个元素
    if (n == 1) {
        return;
    }
    createHeap(a, n);
    for (int i = n; i >= 2; i--) {
        int temp = a[i];
        a[i] = a[1];
        a[1] = temp;
        heapify(a, i - 1, 1);
    }
}

2.2 堆排序的性能分析

创建堆的性能分析
删除堆顶元素的性能分析

2.2.1 创建堆的性能分析

堆化过程中，我们只需要对第1到n/2个节点进行堆化。而每个节点堆化的过程中，需要比较和交互的节点个数，跟这个节点的高度K成正比

下图表示了每一层的节点个数和对
应的高度。我们只需要将每个节点的高度求和，得出的就是建堆的时间复杂度。

节点层次和高度示意图

我们将每个非叶子节点的高度求和，就是下面的这个公式

将公式左右两侧都乘以2，得到另外一个公司S2，然后将用S2-S1,可以得到S

S的中间部分是一个等比数列，所以最后可以用等比数列求和公式来计算，最终的结果就是下面图中画的这个样子。

因为h=log2(n),代入公式S，就得到了S=O(n)，所以，建堆的时间复杂度就是O(n)

2.2.2 删除堆顶元素的性能分析

删除的算法复杂度推算过程和建堆的复杂度推算过程类似，最后计算出来的复杂度是O(nlogn)。

所以堆排序总的时间复杂度是O(nLogn).

源码

完整的源码和测试用例，请查看github之堆和堆排序

说明

文中图片来源：极客时间，王争《数据结构与算法之美》