机器学习作业3-神经网络
一、算法目标
通过神经网络,识别图片上的阿拉伯数字
作业材料中提供了原始图片素材,并标记了观察的值
每一张小图,宽高20 * 20,用灰度值表示。
二、逻辑回归算法实现
1.加载数据
import matplotlib.pyplot as plt
import numpy as np
import scipy.io as sio
import matplotlib
import scipy.optimize as opt
from sklearn.metrics import classification_report#这个包是评价报告
def load_data(path, transpose=True):
data = sio.loadmat(path)
y = data.get('y') # (5000,1)
y = y.reshape(y.shape[0]) # make it back to column vector
X = data.get('X') # (5000,400)
if transpose:
# for this dataset, you need a transpose to get the orientation right
X = np.array([im.reshape((20, 20)).T for im in X])
# and I flat the image again to preserve the vector presentation
X = np.array([im.reshape(400) for im in X])
return X, y
X, y = load_data('ex3data1.mat')
print(X.shape)
print(y.shape)
(5000, 400)
(5000,)
定义用到的绘图函数
def plot_an_image(image):
# """
# image : (400,)
# """
fig, ax = plt.subplots(figsize=(1, 1))
ax.matshow(image.reshape((20, 20)), cmap=matplotlib.cm.binary)
plt.xticks(np.array([])) # just get rid of ticks
plt.yticks(np.array([]))
#绘图函数
简单的观察下效果
pick_one = np.random.randint(0, 5000)
plot_an_image(X[pick_one, :])
plt.show()
print('this should be {}'.format(y[pick_one]))
'y'数据集里存放了图片对应的实际值
从5000条数据里随机选100条数据显示,观察效果
def plot_100_image(X):
""" sample 100 image and show them
assume the image is square
X : (5000, 400)
"""
size = int(np.sqrt(X.shape[1]))
# sample 100 image, reshape, reorg it
sample_idx = np.random.choice(np.arange(X.shape[0]), 100) # 100*400
sample_images = X[sample_idx, :]
fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))
for r in range(10):
for c in range(10):
ax_array[r, c].matshow(sample_images[10 * r + c].reshape((size, size)),
cmap=matplotlib.cm.binary)
plt.xticks(np.array([]))
plt.yticks(np.array([]))
#绘图函数,画100张图片
plot_100_image(X)
plt.show()
2. 先用逻辑回归处理数据
下面这段话非常重要,是数字识别的核心逻辑
raw_y表示结果集,存储了5000条数据的结果,单一维度的机器学习算法并不能识别出多种可能。这里分两步走
- 把0~9的结果集转成bool型,转化成逻辑回归问题,astype方法转成0/1值
- 用10个向量分别存储单一数值的结果集,每一个向量用来训练单一数值的模型
raw_X, raw_y = load_data('ex3data1.mat')
print(raw_X.shape)
print(raw_y.shape)
(5000, 400)
(5000,)
# add intercept=1 for x0 (增加截距,即theta0的值)
X = np.insert(raw_X, 0, values=np.ones(raw_X.shape[0]), axis=1)#插入了第一列(全部为1)
X.shape
1556
(5000, 401)
# matlab的角标从1,开始用10代表0
# y have 10 categories here. 1..10, they represent digit 0 as category 10 because matlab index start at 1
# I'll ditit 0, index 0 again
y_matrix = []
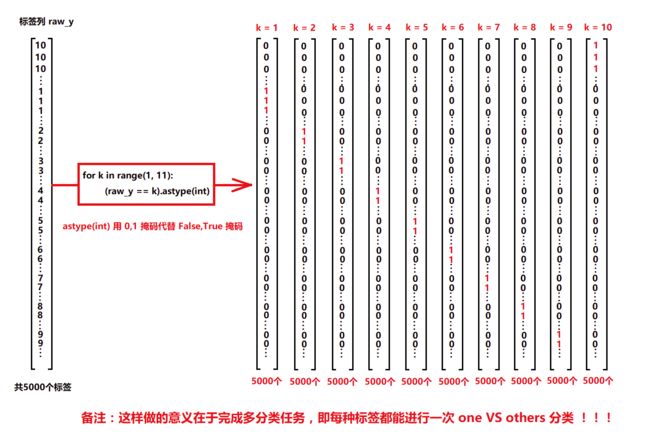
# 重点,这里把[5000]的数据编成10 * 5000的矩阵,用来一次性训练0~9的所有参数集。要体会使用矩阵运算的魅力。
for k in range(1, 11):
y_matrix.append((raw_y == k).astype(int)) # 见配图 "向量化标签.png"
# last one is k==10, it's digit 0, bring it to the first position,最后一列k=10,都是0,把最后一列放到第一列
y_matrix = [y_matrix[-1]] + y_matrix[:-1]
y = np.array(y_matrix)
y.shape
# 扩展 5000*1 到 5000*10
# 比如 y=10 -> [0, 0, 0, 0, 0, 0, 0, 0, 0, 1]: ndarray
# """
(10, 5000)
2. 训练一维模型
实现基础函数:损失函数、梯度下降等
def cost(theta, X, y):
''' cost fn is -l(theta) for you to minimize'''
return np.mean(-y * np.log(sigmoid(X @ theta)) - (1 - y) * np.log(1 - sigmoid(X @ theta)))
def regularized_cost(theta, X, y, l=1):
'''you don't penalize theta_0'''
theta_j1_to_n = theta[1:]
regularized_term = (l / (2 * len(X))) * np.power(theta_j1_to_n, 2).sum()
return cost(theta, X, y) + regularized_term
def regularized_gradient(theta, X, y, l=1):
'''still, leave theta_0 alone'''
theta_j1_to_n = theta[1:]
regularized_theta = (l / len(X)) * theta_j1_to_n
# by doing this, no offset is on theta_0
regularized_term = np.concatenate([np.array([0]), regularized_theta])
return gradient(theta, X, y) + regularized_term
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def gradient(theta, X, y):
'''just 1 batch gradient'''
return (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y)
def logistic_regression(X, y, l=1):
"""generalized logistic regression
args:
X: feature matrix, (m, n+1) # with incercept x0=1
y: target vector, (m, )
l: lambda constant for regularization
return: trained parameters
"""
# init theta
theta = np.zeros(X.shape[1])
# train it
res = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient,
options={'disp': True})
# get trained parameters
final_theta = res.x
return final_theta
def predict(x, theta):
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int)
先训练一维参数,对"0" or "1" 做判断,y.shape是(10, 5000)
t0 = logistic_regression(X, y[0])
y.shape
y_pred = predict(X, t0)
print(t0.shape)
print('Accuracy={}'.format(np.mean(y[0] == y_pred)))
(401,)
Accuracy=0.9974
3. train k model(训练k维模型)
和1维模型的训练类似,循环10次
k_theta = np.array([logistic_regression(X, y[k]) for k in range(10)])
print(k_theta.shape)
(10, 401)
k_theta是10组向量,每组向量401个参数,与一个图片的400个像素对应,多出来的一个是截距,即初始向量
4. k维预测
- think about the shape of k_theta, now you are making
- after that, you run sigmoid to get probabilities and for each row, you find the highest prob as the answer
prob_matrix = sigmoid(X @ k_theta.T)
np.set_printoptions(suppress=True)
#预测的结果集:
prob_matrix
array([[0.99577491, 0. , 0.00053534, ..., 0.00006469, 0.0000391 ,
0.00172015],
[0.99834696, 0.0000001 , 0.0000561 , ..., 0.00009682, 0.0000029 ,
0.00008487],
[0.99139841, 0. , 0.00056797, ..., 0.00000655, 0.02655473,
0.00197369],
...,
[0.00000068, 0.04139552, 0.00321035, ..., 0.00012717, 0.00297688,
0.70767493],
[0.00001843, 0.00000013, 0.00000009, ..., 0.00164739, 0.06816852,
0.8611639 ],
[0.02879718, 0. , 0.00012972, ..., 0.36613378, 0.00497566,
0.14818646]])
y_pred = np.argmax(prob_matrix, axis=1)#返回沿轴axis最大值的索引,axis=1代表行
y_pred
array([0, 0, 0, ..., 9, 9, 7]) -->(5000,)
y_answer = raw_y.copy()
y_answer[y_answer==10] = 0 #前面raw_y中'10'表示'0'
print(classification_report(y_answer, y_pred))
precision recall f1-score support
0 0.97 0.99 0.98 500
1 0.95 0.99 0.97 500
2 0.95 0.92 0.93 500
3 0.95 0.91 0.93 500
4 0.95 0.95 0.95 500
5 0.92 0.92 0.92 500
6 0.97 0.98 0.97 500
7 0.95 0.95 0.95 500
8 0.93 0.92 0.92 500
9 0.92 0.92 0.92 500
accuracy 0.94 5000
macro avg 0.94 0.94 0.94 5000
weighted avg 0.94 0.94 0.94 5000
看上表,‘0’、‘1’、‘6’预测的准确率比较高,'5'、'8'、'9'准确率比较低
三、神经网络模型
上面使用普通的逻辑回归来训练模型,神经网络其实就是多层逻辑回归
这里没有对神经网络模型进行训练,直接使用了已经训练好的参数来观察预测结果,猜测可能是降低难度,或者担心学生电脑跑步起来复杂的模型
加载模型参数,可以看到中间层是25个神经元,整个流程是
5000条数据->拟合出25组参数-->继续拟合出10组参数,分别用来预测0~9
中间加一层,真的就这么神奇吗???
def load_weight(path):
data = sio.loadmat(path)
return data['Theta1'], data['Theta2']
theta1, theta2 = load_weight('ex3weights.mat')
theta1.shape, theta2.shape
((25, 401), (10, 26))
因为在数据加载函数中,原始数据做了转置。然而,转置的数据与给定的参数不兼容,因为这些参数是由原始数据训练的。 所以为了应用给定的参数,我需要使用原始数据(不转置)??
这里说的要点啰嗦,大意应该是数据的存储结构吧,anyway,这不是重点,不丛深究
X, y = load_data('ex3data1.mat',transpose=False)
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # intercept
X.shape, y.shape
((5000, 401), (5000,))
feed forward prediction(前馈预测)
z2 = a1 @ theta1.T # (5000, 401) @ (25,401).T = (5000, 25)
z2.shape
z2 = np.insert(z2, 0, values=np.ones(z2.shape[0]), axis=1)
a2 = sigmoid(z2)
z3 = a2 @ theta2.T
a3 = sigmoid(z3)
y_pred = np.argmax(a3, axis=1) + 1 # numpy is 0 base index, +1 for matlab convention,返回沿轴axis最大值的索引,axis=1代表行
y_pred.shape
总结
虽然人工神经网络是非常强大的模型,但训练数据的准确性并不能完美预测实际数据,在这里很容易过拟合。
print(classification_report(y, y_pred))
precision recall f1-score support
1 0.97 0.98 0.97 500
2 0.98 0.97 0.97 500
3 0.98 0.96 0.97 500
4 0.97 0.97 0.97 500
5 0.98 0.98 0.98 500
6 0.97 0.99 0.98 500
7 0.98 0.97 0.97 500
8 0.98 0.98 0.98 500
9 0.97 0.96 0.96 500
10 0.98 0.99 0.99 500
accuracy 0.98 5000
macro avg 0.98 0.98 0.98 5000
weighted avg 0.98 0.98 0.98 5000
对比上面的普通的逻辑回归,或者说是没有中间层的神经网络,准确率确实提升了不少
print(classification_report(y_answer, y_pred))
precision recall f1-score support
0 0.97 0.99 0.98 500
1 0.95 0.99 0.97 500
2 0.95 0.92 0.93 500
3 0.95 0.91 0.93 500
4 0.95 0.95 0.95 500
5 0.92 0.92 0.92 500
6 0.97 0.98 0.97 500
7 0.95 0.95 0.95 500
8 0.93 0.92 0.92 500
9 0.92 0.92 0.92 500
accuracy 0.94 5000
macro avg 0.94 0.94 0.94 5000
weighted avg 0.94 0.94 0.94 5000