理解numpy中array和pytorch中tensor的操作是开始科学运算的第一步!
首先明白维度的感念:
维度
我们通常能听到的都是2D, 3D,其实这边的D就是dimension的含义即维度。2D,我们通常理解为是平面,如我们最熟悉的直角坐标系就是平面坐标系,还有极坐标系。而3D呢,就是在平面的基础上增加了一维——高度,从而使平面的物体立起来了,同样3D也有耳熟能详的坐标系——3维坐标系。
更官方的解释呢:维度(Dimension),又称为维数,是数学中独立参数的数目。在物理学和哲学的领域内,指独立的时空坐标的数目。0维是一个无限小的点,没有长度。1维是一条无限长的线,只有长度。2维是一个平面,是由长度和宽度(或部分曲线)组成面积。3维是2维加上高度组成体积。4维分为时间上和空间上的4维,人们说的4维通常是指关于物体在时间线上的转移。(4维准确来说有两种。1.四维时空,是指三维空间加一维时间。2.四维空间,只指四个维度的空间。)四维运动产生了五维。
从哲学角度看,人们观察、思考与表述某事物的“思维角度”,简称“维度”。例如,人们观察与思考“月亮”这个事物,可以从月亮的“内容、时间、空间”三个思维角度去描述;也可以从月亮的“载体、能量、信息”三个思维角度去描述。这边的维度其实也可以理解为角度,从不同的方面去看待、确定一个事物。
所以代数上来说,维度其实是数学里在表示方面的一个重要的概念,它反映的是一个空间的本质性质。
科学计算中维度的概念
从二维点位置->编程中的坐标系
维度的考量主要集中在矩阵的运算上。首先我们来看一个元素:4,其实它就是一个点,可以被认为是0维的。但往往我们不会只有一个元素。我们最常见的是编程中的数组,如[1,2,3,4],这个是由多个元素构成的,它的维度就是一维的,这个我们也比较好理解。
而二维是什么呢?我们能直观理解的二维是平面坐标系的那种:(1,3), (4,5)...即给一个x,一个y,那么在平面中就可以在直角坐标系下确定这个点(物)。现在我们规整下这些坐标点[ (1, 3), (4, 5) ],从这个角度上离我们的矩阵,或是数组好像还是有点远。那么我们继续变形。
如果我们需要画出坐标系中有哪些点的话, 1.第一种做法就是跟上述一样, 把点都存一个vector中[ (1, 3), (4, 5) ],然后遍历,再在坐标系中点出。2.第二种呢,就是在坐标系中把所有的位置都列出来,如果有点存在就把它标出来,即跟我们列出迷宫地图一样,先把地图画出来,然后再把宝藏标出来。所以上述的两个点可以理解为。在给出了map[20][20]的地图上,(1, 3)和(4, 5)位置为true, 即map[1][3] = 1, map[4][5] = 1,其他位置map[x][y] = 0,所以这样我们就从[(1, 3), (4, 5)]==> 用map形式表现出了这两个点,两者成功在二维上进行了转换。接下来我们就来分析这个二维的map。
数组,在编程中,我们都不陌生,如int arr[50][50],虽然可以通过这个二维的数组,根据val的不同来表示三维的量,但是我们这边不把它这么理解,仅是当做bool arr[50][50]来理解维度上的概念。===>同样,面对numpy中的array我们也是这么个理解。
import numpy as np
import torch
x = np.random.randint(2, size = (2,3))
print(x)
y = torch.randint(2, size = (2, 3))
print(y)
'''
[[0 1 1]
[1 0 1]]
tensor([[1, 0, 1],
[0, 0, 1]])
'''
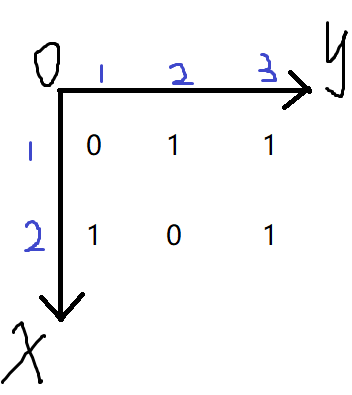
我们从numpy的x上理解,这边是创建了一个2*3的矩阵,其中x[0][1], x[0][2], x[1][0], x[0][2]全1,其余为0,输入x.shape得到的结果是(2, 3),有两项,跟我们从map的理解上是一致的,这个地图map拥有长和宽两个维度。
然后我们从编程中观察这个2*3的矩阵或是叫数组,可以发现x[a][b]第一个[]中的内容a范围是从0-1的,第一个[]中的内容b范围是从0-2的,0的话学编程的人都能很快的理解,而第二个的范围却不太那么肯定。为什么呢?因为它跟我们普通认知的直角坐标系不一致。下面我们把x画出来(不改变输出显示的形式,而是让坐标系去适应这种表现形式)。
为什么是这样画的呢?首先明确的原则是,不改变输出显示的形式,而是让坐标系去适应这种输出形式,因此输出长啥样,我们坐标系只能去适应。由于我们碰到有x,有y的时候,习惯上把第一个出现的当作x,第二个当作y,所以就有了第一个[]为x,第二个[]为y。
好了,现在我们确定好坐标系长什么样了。接下来就是具体理解dim的含义了
编程中坐标系->科学计算中array的dim
想必大家在学习numpy或者torch的时候都被各种函数方法中的dim参数折磨过,感觉怎么理解都有问题,不敢自己使用。因此,这边就是解决,这些函数中的dim到底是怎么确定的
比如我们创建一个高维的array
A = torch.randint(2, size = (1,2,3,4))
'''
tensor([[[[0, 0, 1, 0],
[1, 1, 0, 1],
[0, 0, 0, 0]],
[[0, 0, 1, 1],
[1, 1, 1, 0],
[0, 1, 0, 0]]]])
'''
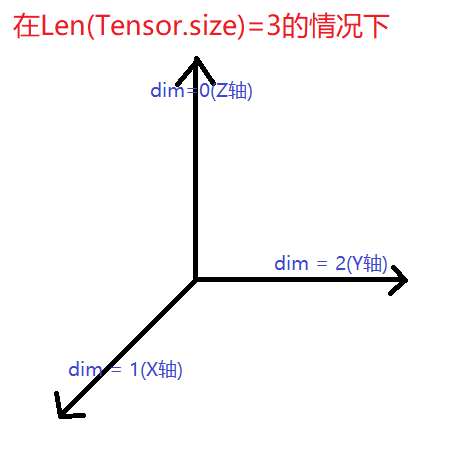
举个我自己最初理解dim的笨方法:硬记x为第一维(dim = 0), y为第二维(dim = 1)
实际上这种记法是比较低效的,最好的方法是我们怎么定义这个array就怎么记,比如我们这边创建的是一个size=(1, 2, 3, 4),输出len(A.shape)为4,可以看到这就是个4维的tensor,那么我们顺理成章地就把把各个维度依次定义出来了。如dim = 0地指的就是size = 1的那层,dim = 1就是指size = 2的那层,依次类推。这样说可能有点抽象,因此我们回归简单的。
B = torch.randint(2, size = (3, 2))
print(B)
'''
tensor([[1, 0],
[1, 1],
[0, 0]])
'''
按照我们刚的定义,dim=0就是size=3的这一层,也就是我们坐标系中的X轴orX面。
好了,想必大家这个时候还不知道我在说什么。接下来就带大家来测试函数。
测试dim在函数参数中的定义
提前指出把:要注意函数介绍中dim指的是"沿着dim这个维度"or"删除、增加....dim这个维度(在dim这个维度上进行维度修改)"
规约计算
一般是指分组聚合计算,表现结果就是会进行维度压缩
sum
沿着dim累加元素
C = torch.randint(5, size = (2, 5))
print(C)
'''
tensor([[2, 3, 3, 4, 0],
[1, 0, 2, 4, 4]])
'''
print(C.sum(dim = 0))
print(C.sum(dim = 1))
'''
tensor([3, 3, 5, 8, 4])
tensor([12, 11])
'''
可以看到sum就是比较典型的"沿着dim"的例子,当dim = 0时就沿着dim = 0即x轴进行累加,由于sum这个函数会进行维度的压缩,所以最后的结果为tensor([3, 3, 5, 8, 4])
cumprod
通过dim指定沿着某个维度计算累积
其他的函数还有cumsum、prod、sum,实际上两者是相同的,还有mean、median、var、std、min、max
#
x = torch.Tensor([
[2,3,4,5,6],
[9,8,7,6,5,]
])
print(torch.cumprod(x, dim = 0))
print(torch.cumprod(x, dim = 1))
'''
tensor([[ 2., 3., 4., 5., 6.],
[18., 24., 28., 30., 30.]])
tensor([[2.0000e+00, 6.0000e+00, 2.4000e+01, 1.2000e+02, 7.2000e+02],
[9.0000e+00, 7.2000e+01, 5.0400e+02, 3.0240e+03, 1.5120e+04]])
'''
# min
x = torch.Tensor([
[2,3,4,5,6],
[9,8,7,6,5,]
])
print(torch.min(x, dim = 0))
print(torch.min(x, dim = 1))
'''
torch.return_types.min(
values=tensor([2., 3., 4., 5., 5.]),
indices=tensor([0, 0, 0, 0, 1]) )
torch.return_types.min(
values=tensor([2., 5.]),
indices=tensor([0, 4]) )
'''
# mean
x = torch.Tensor([
[2,3,4,5,6],
[9,8,7,6,5,]
])
print(torch.mean(x, dim = 0))
print(torch.mean(x, dim = 1))
'''
tensor([5.5000, 5.5000, 5.5000, 5.5000, 5.5000])
tensor([4., 7.])
'''
索引、切片、连接
squeeze,unsqueeze
unsqueeze关键字:参数dim指定在第几个维度增加"[]",以提升维度
squeeze: unsqueeze的逆操作,删除dim指定的维度
unsqueeze
D = torch.Tensor( [1, 2, 3, 4, 5] )
y = D.unsqueeze(dim = 0)
print(y, y.shape)
'''
tensor([[1., 2., 3., 4., 5.]]) torch.Size([1, 5])
'''
y = D.unsqueeze(dim = 1)
print(y.shape)
'''
tensor([[1.],
[2.],
[3.],
[4.],
[5.]]) torch.Size([5, 1])
'''
可以看到的是dim = 0的时候就是在dim = 0 维度上增加了一维, 使得变成了[1, 5]。第二个是在dim=1的位置加了一维变成了[5, 1] (这也就是为什么很多书上会说其实就是在dim维度上加了1)
▲这个典型就是要区分: 在dim维度上 和 沿着dim维度了
squeeze
F = torch.Tensor( [ [0, 2, 3, 4],
[22, 33, 44 ,55]
])
y = torch.squeeze(F, dim = 0)
print(y, y.shape)
'''
tensor([[ 0., 2., 3., 4.],
[22., 33., 44., 55.]]) torch.Size([2, 4])
'''
y = torch.squeeze(F, dim = 1)
print(y, y.shape)
'''
tensor([[ 0., 2., 3., 4.],
[22., 33., 44., 55.]]) torch.Size([2, 4])
'''
这边变换不大的原因是因为dim上没有size=1可以删除
split
按(沿着)dim维度将tensor分成n个部分
x = torch.Tensor([
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
])
print(x)
print(torch.split(x, 5, dim = 1))
# 指定划分列表,表示依次有1,2,3,4个长度 (总和得跟dim维度上元素个数相同)
print(torch.split(x, [1,2,3,4], dim = 1))
'''
tensor([[ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.],
[10., 9., 8., 7., 6., 5., 4., 3., 2., 1.]])
(tensor([ # 可以看到这个是在x[:][6]的地方将tensor切成了两个
[ 1., 2., 3., 4., 5.],
[10., 9., 8., 7., 6.]
]),
tensor([
[ 6., 7., 8., 9., 10.],
[ 5., 4., 3., 2., 1.]
]))
(tensor([[ 1.],
[10.]]), tensor([[2., 3.],
[9., 8.]]), tensor([[4., 5., 6.],
[7., 6., 5.]]), tensor([[ 7., 8., 9., 10.],
[ 4., 3., 2., 1.]]))
'''
unbind
删除某个维度后,返回所有切片组成的元组
x = torch.rand(1,2,3)
# x = torch.rand(size=(1,2,3))
print(x, x.shape)
out = torch.unbind(x, dim = 1)
print(out, len(out))
'''
tensor([
[
[0.3631, 0.6672, 0.9489],
[0.4944, 0.1606, 0.6122]
]
]) torch.Size([1, 2, 3])
(
tensor([[0.3631, 0.6672, 0.9489]]), torch.Size([1, 3])
tensor([[0.4944, 0.1606, 0.6122]]) torch.Size([1, 3])
) 2
'''
x = torch.Tensor([
[[1,2,3,4,],
[5,6,7,8],
[9,10,11,12]],
[[13,14,15,16],
[17,18,19,20],
[21,22,23,24]]
])
print(x, x.shape)
out = torch.unbind(x, dim = 1)
print(out, len(out))
print(out[0].shape)
'''
tensor([
[[1,2,3,4,],
[5,6,7,8],
[9,10,11,12]],
[[13,14,15,16],
[17,18,19,20],
[21,22,23,24]]
]) torch.Size([2, 3, 4])
(tensor([
[ 1., 2., 3., 4.],
[13., 14., 15., 16.]]),
tensor([
[ 5., 6., 7., 8.],
[17., 18., 19., 20.]]),
tensor([
[ 9., 10., 11., 12.],
[21., 22., 23., 24.]]))
删除dim = 1, 把size[1] = 3的tensor拆成了3个tensor
不要记这个: 因为dim0为z轴, dim1为x轴, dim2为y轴,所以删除dim1就是删除x轴,最后得到的就是yOz平面
'''
cat、stack
通过关键字dim指定按哪个维度拼接
x = torch.randint(1, 100, size=(2,3))
print(x)
y = torch.randint(1, 100, size=(2,3))
print(y)
res = torch.cat((x, y), dim = 1)
print(res)
'''
tensor([[71, 56, 44],
[64, 30, 87]])
tensor([[39, 56, 63],
[68, 28, 65]])
tensor([[71, 56, 44, 39, 56, 63],
[64, 30, 87, 68, 28, 65]])
'''
# 加强高维理解
x = torch.randint(1, 100, size=(2,3,4))
print(x)
y = torch.randint(1, 100, size=(2,3,4))
print(y)
res = torch.cat((x, y), dim = 1)
print(res)
'''
tensor([[[81, 79, 10, 8],
[47, 30, 48, 35],
[10, 57, 68, 88]],
[[33, 51, 60, 97],
[27, 14, 83, 51],
[51, 54, 79, 65]]])
tensor([[[85, 9, 95, 95],
[29, 99, 12, 8],
[32, 8, 3, 84]],
[[13, 24, 46, 20],
[86, 83, 72, 10],
[76, 33, 79, 48]]])
tensor([[[81, 79, 10, 8],
[47, 30, 48, 35],
[10, 57, 68, 88],
[85, 9, 95, 95],
[29, 99, 12, 8],
[32, 8, 3, 84]],
[[33, 51, 60, 97],
[27, 14, 83, 51],
[51, 54, 79, 65],
[13, 24, 46, 20],
[86, 83, 72, 10],
[76, 33, 79, 48]]]) torch.Size([2, 6, 4])
dim=1即沿元素为3的方向上延伸,所以结果变成了6
不要记:也可以理解为沿x轴方向
'''
官方文档: https://pytorch.org/docs/stable/generated/torch.cat.html?highlight=cat#torch.cat
总结
正确理解姿势
dim是指tensor在shape上的顺序(可以这么理解),如x的shape是2x3x4,也就是[2, 3, 4]。故可以这样一一对应来。
比如dim = 1就是按具有3个元素的那个轴操作,从而不用死记硬背那些dim = 0是对列操作还是对行操作了。
强记三维
但还是不提倡强记,因为一旦高维就理解不了了。
附:
关于size的设置
在ones、rand等函数上,size = (2,3,4),我们在C++数组中int arr[x][y][z]的理解是然后z为4, 但实际上在科学运算中size = (2,3,4)的矩阵是有4个的矩阵叠加而成,这边是要区分的
>>> import numpy as np
>>> a = np.random.randint(1, 100, [2, 3, 4])
>>> a
array([[[26, 36, 31, 21],
[74, 59, 79, 32],
[77, 94, 81, 32]],
[[72, 76, 85, 93],
[66, 34, 80, 12],
[99, 17, 98, 23]]])
x = torch.randint(1, 100, size=(2,3,4))
print(x)
print(x[1][2][3]) # 高度索引为1的, 在x = 2, y = 3的元素就是76
'''
tensor([[[63, 54, 57, 17],
[78, 64, 76, 44],
[96, 3, 59, 37]],
[[86, 3, 92, 84],
[89, 36, 8, 79],
[10, 87, 15, 76]]])
tensor(76)
'''
x = torch.randint(1, 100, size=(2,3,4,2))
print(x)
'''
tensor([[[[29, 50],
[50, 69],
[95, 70],
[21, 35]],
[[58, 65],
[15, 53],
[96, 25],
[11, 75]],
[[12, 71],
[36, 12],
[71, 92],
[87, 47]]],
[[[43, 89],
[88, 22],
[61, 56],
[47, 97]],
[[71, 7],
[44, 88],
[54, 32],
[15, 65]],
[[96, 22],
[90, 78],
[30, 85],
[65, 57]]]])
'''
pytorchAPI:
https://pytorch.org/docs/stable/torch.html#torch.arange