【高考地位】
立体几何中的二面角是一个非常重要的数学概念,求二面角的大小更是历年高考的热点问题,每年各省、市的高考试题中几乎都会出现此类题型。其求解的策略主要有三种方法:其一是定义法,即按照二面角的定义进行求解;其一是射影法,即找其中一个平面的垂线;其一是空间向量法,即建立直角坐标系进行求解. 在高考中常常以解答题出现,其试题难度属中高档题.
【方法点评】
方法一 定义法
使用情景:空间中面面角的求法
解题步骤:
第一步 首先分别在两个平面中找出与交线垂直的直线;
第二步 然后运用平移或解三角形的知识求其夹角;
第三步 得出结论.
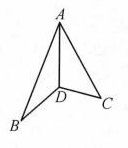
【例】. 在边长为的正三角形中,于,沿折成二面角后,,这时二面角的大小为___.
【解析】
根据已知条件知为正三角形边中点,且,;
所以为二面角的平面角,连接
由得为正三角形;
所以
故二面角的大小为.
【总结】
本题考查二面角平面角的概念及求法,属中档题.弄清图形折叠前后的变化,认识到等边三角形的高线也是中线是解题的关键,根据已知条件能够说明为二面角的平面角,连接,从而容易说明为正三角形,从而得出二面角的大小为.
方法二 射影法
使用情景:空间中面面角的求法
解题步骤:
第一步 首先求出其中一个平面的垂线;
第二步 然后过垂足作交线的垂线即可得到二面角的平面角;
第三步 运用解三角形等相关知识即可求出其大小.
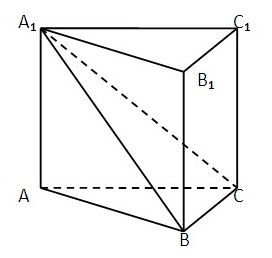
【例】. 如图所示,在直三棱柱中,平面侧面,且.
(1)求证:;
(2)若直线与平面所成角的正弦值为,求锐二面角的大小.
【解析】
(1)证明:如图,取的中点,连接.
因,则,
由平面侧面,
且平面侧面,
得平面,又平面,
所以
因为三棱柱是直三棱柱,
则底面,所以.
又,从而侧面,
又侧面,故.
(2)连接,由(1)可知平面,则是在平面内的射影,
所以即为直线与平面所成的角,
因为直线与平面所成角的正弦值为,则,
在等腰直角中,,且点是中点,
且,,
,过点作于点,连接,
由(1)知平面,则,且
即为二面角的一个平面角.
且中,,
又,
,且二面角为锐二面角,
,即二面角的大小为.
方法三 空间向量法
使用情景:空间中面面角的求法
解题步骤:
第一步 首先建立适当的直角坐标系并写出相应点的空间直角坐标;
第二步 然后求出两个平面的法向量;
第三步 再利用即可得出结论.
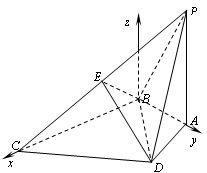
【例1】 如图,在四棱锥中,底面,,为等边三角形,,,为的中点.
(1)求;
(2)求平面与平面所成二面角的正弦值.
【解析】
(1)连接, 因为底面,平面,所以,
又因为,,
所以底面,
因为平面,
所以,
因为为等边三角形,
所以.
又已知,,
可得.
(Ⅱ)分别以,所在直线为,轴,过且平行的直线为轴建立空间直角坐标系.
则,,,.
由题意可知平面的法向量为.
设平面的法向量为,
则,得则.
.
所以平面与平面所成二面角的正弦值.
【总结】本题主要考查了线面垂直的判定定理与性质定理、空间向量求立体几何问题、推理论证能力、空间想象能力和推理论证能力,考查学生综合应用知识的能力和应变能力,属综合题.其解题过程中最容易出现以下错误:
其一是不能准确找出线线关系,尤其是线线垂直、线面垂直的关系,进而不能正确地求出所得的结果;
其二是对于第二问不能正确地运用空间向量求立体几何问题,进而导致失误.
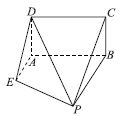
【例2】、如图, 已知矩形所在平面垂直于直角梯形所在平面, 平面平面,且,,,且. 求二面角的余弦值.
【解析】
以为原点,,,所在直线分别为轴,轴,轴建立坐标系,
平面
平面的法向量,另外,,,
,
设平面的法向量,则,令,得
,
又为锐二面角,所以二面角的余弦值为.
【总结】:本题考查平面与平面垂直的证明,属中档题.解题时要认真审题,注意合理地进行等价转化,合理地运用向量法进行解题.