程序 = 数据结构 + 算法
1.数据结构和算法
(1)数据结构
- 数据结构是由数据和结构两方面组成。
- 比如:数据就是姓名、年龄和性别,结构就是姓名、年龄和性别的关系。
- 数据结构指的是数据与数据之间的逻辑关系。
(2)数据结构有什么用
解决问题,如何高效(多快好省)的从已知数据求解未知数据。
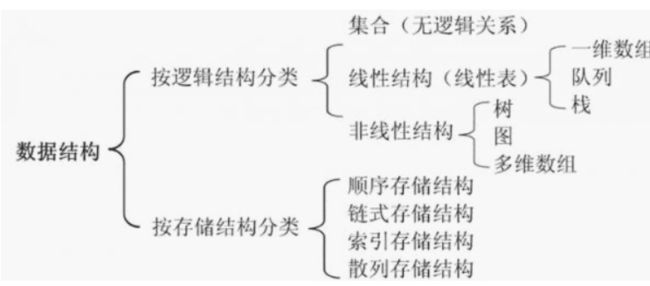
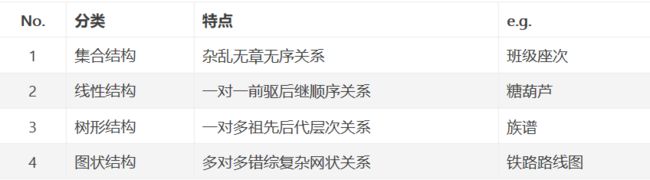
(3)数据结构的分类
顺序表和链表都是线性表,用线性表实现队列和栈,所以队列和栈是线性结构。
(2)算法
<1>算法是什么
算法指的是解决特定问题的步骤和方法。
<2>算法有什么用?
解决问题,如何高效(多快好省)的从已知数据求解未知数据。
<3>算法的好坏?
- 准确性:必须能够解决这个问题
- 健壮性:这个算法编写的程序要求在任何情况下不能崩溃
运行效率体现在两方面: - 时间复杂度:算法的运行时间
- 空间复杂度:运行算法所需的内存空间大小
2.时间复杂度和空间复杂度
(1)时间复杂度
<1>定义
时间复杂度主要度量基本操作重复执行的次数,是输入规模和基本操作的数量关联,随着输入规模扩大的增长量。
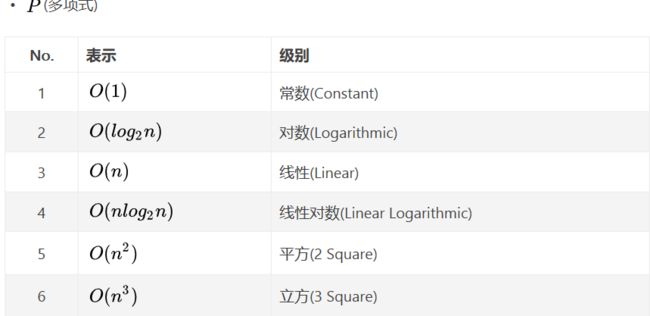
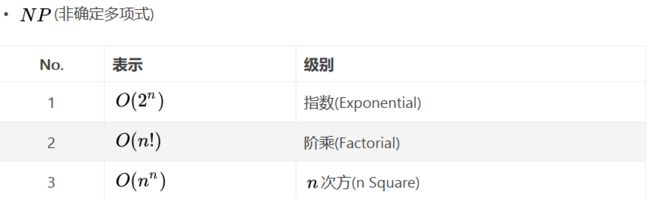
<2>如何表示时间复杂度
用O记号表示算法的时间性能。
<3>如何计算时间复杂度?(***)
- 1.找出基本语句(执行次数最多的语句):
最内层循环的循环体 - 2.计算基本语句的执行次数的数量级:
只保留最高次幂,忽略低次幂和最高次幂的系数 - 3.用大O记号表示算法的时间性能:
int i=1;
int n =100;
while(i序列找数-招商银行信用卡中心2018秋
思路:(1)双重循环
(2)求和
(2)空间复杂度
<1>空间复杂度是什么
空间复杂度是指运行完一个程序所需内存的大小。
<2>如何表示空间复杂度
程序执行时所需存储空间包括以下两部分:
- 固定部分。这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间(即代码空间)、数据空间(常量、简单变量)等所占的空间。这部分属于静态空间。
- 可变空间。这部分空间的主要包括动态分配的空间,以及递归栈所需的空间等。这部分的空间大小与算法有关。
3.顺序表
(1)概念
顺序表是用一组地址连续的存储单元依次存储线性表中的各个元素,使线性表中在逻辑结构上相邻的数据元素存储在相邻的物理存储单元中。
数组的缺点:大小(元素个数)不能改变,不能适用元素个数变化的情况。
数组可以看作无法改变大小的顺序表。
(2)使用
顺序表通过一个结构体和结构体对应的接口使用。
(3)实现
<1>定义结构
typedef int SeqType; //存储单元类型
typedef struct{
SeqType *elem; //存储空间基地址
int size; //当前长度
} List;
定义一个存储单元类型SeqType是为了使顺序表适和更多数据类型,使用的时候修改SeqType类型即可。
<2>定义操作
- 1.初始化顺序表
为什么要初始化?因为局部变量默认初始化为随机值。
怎么初始化?把结构体变量成员赋值为合法的初始值。
void list_init(List* seq);
- 2.添加元素
int sqlist_append(SqList* plist,SeqType value);
int sqlist_prepend(SqList* plist,SeqType value);
- 3.获取元素
SeqType sqlist_get(SqList* plist,int index);
SeqType* sqlist_at(SqList* plist,int index);//可以修改元素
- 4.获取元素个数
int sqlist_size(SqList* plist);
- 5.插入元素
void sqlist_insert(SqList* plist,int index,SeqType value);
- 6.删除元素
void sqlist_remove(SqList* plist,int index);
- 7.销毁顺序表
void sqlist_destroy(SqList* plist);
- 8.增加容量
int capacity; //当前分配的存储容量
- 9.遍历
typedef void (*SqList_Traversal)(const SeqType* value);
void sqlist_traverse(SqList* plist,SqList_Traversal fp);
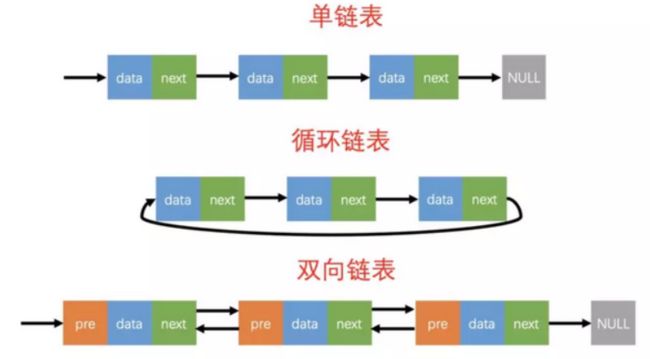
4.链表
(1)概念
<1>顺序表的缺点
- 添加和删除操作需要移动元素。
- 当数据量特别大的情况,可能没有连续的内存可使用。
<2>定义
别名链式存储结构或单链表,用于存储逻辑关系为 "一对一" 的数据。与顺序表不同,链表不限制数据的物理存储状态。顺序表通过连续的地址建立元素之间前后连接关系,链表通过指针方式建立元素之间前后连接关系。
- 首结点:存放第一个有效数据的结点。
- 头结点:在单链表的第一个结点之前附设一个结点,它没有直接前驱,称之为头结点,头结点的数据域可以不存储任何信息,指针域指向第一个节点(首节点)的地址。头结点的作用是使所有链表(包括空表)的头指针非空。(哨兵)
- 尾结点:存放最后一个有效数据的节点。
- 头指针:指向头节点的指针
- 尾指针:指向尾结点的指针
(2)使用
链表用法与顺序表相似,只是适用场景有所不同。
(3)实现
<1>定义结构
使用链表存储的数据元素,其物理存储位置是随机的。数据元素随机存储,并通过指针表示数据之间逻辑关系的存储结构就是链式存储结构。
- 链表中每个数据的存储都由以下两部分组成:
1.数据元素本身,其所在的区域称为数据域;
2.指向直接后继元素的指针,所在的区域称为指针域;
单链表与字符串有很多相似之处:单链表的结尾为NULL,字符串的结尾为\0。
typedef int LinkType;
//定义结点
typedef struct _Node{
LinkType val;
struct _Node* next;//指向下一个结点,所以指针类型是struct _Node
}Node;
//定义链表
typedef struct{
Node* head;//头指针
Node* tail;//尾指针
int size;
}List;
<2>定义操作
和顺序表的操作一样。
(4)链表的常用手法
<1>链表的反转
Node* reverse(Node* head){
Node* p=head;
Node* qhead=NULL;
while(NULL !=p){
Node* n=p;
p=p->next;
n->next=qhead;
qhead=n;
}
return qhead;
}
<2>快慢指针
- 形式1:
让快指针先走n步,使快指针领先慢指针n步,然后再和慢指针同时移动,并且速度相等。 - 形式2:
格式
快慢指针判断的固定格式:
struct ListNode* slow=head;
struct ListNode* fast=head;
while(NULL !=fast && NULL !=fast->next)//条件一定要为&&
快指针的速度是慢指针速度的两倍。
中间结点:从同一地点出发,一个的速度是另一个的两倍,快的到达NULL,慢的刚好到达中点。
判断是否存在环:从不同地点出发,一个的速度是另一个的两倍,当快慢指针相等时,存在环。
(5)其他链表
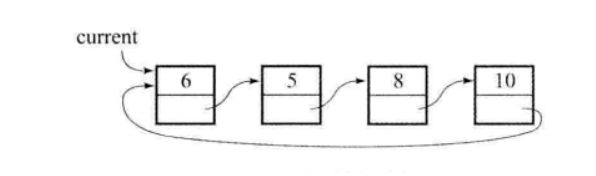
<1>循环单链表
单链表有一个特点只能从头指针开始遍历整个链表,循环单链表可以从任意节点开始遍历整个链表。
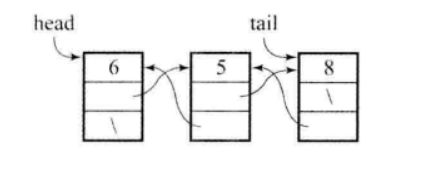
<2>双向链表
单链表在末尾删除节点时,需要获得删除节点前面的一个节点。这需要从队列开头一直遍历到结尾,导致效率瓶颈。双向链表很好的解决这个问题。
注意:
存在两种特殊情况需要处理
1.空链表删除节点
此情况使用断言或者抛出异常。
2.待删除节点的链表中只有一个节点
删除后,需要把头指针和尾指针设置为空
5.栈
在线性表中,顺序表和链表可以访问任意位置结点,在任意位置插入和删除结点。栈和队列是对上述操作加以限制。
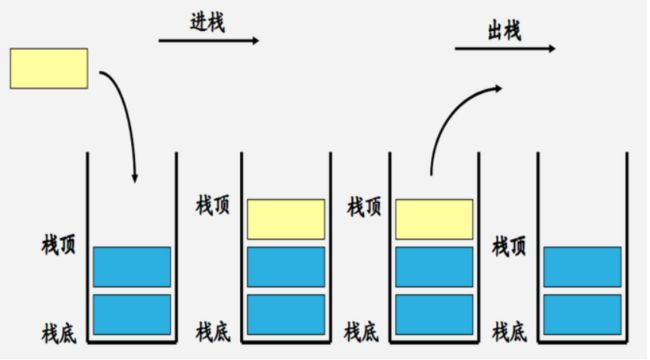
(1)栈是什么
<1>概念
栈是一种只能从表的一端存取数据且遵循 LIFO(先进后出)原则的线性存储结构。
- 栈顶:栈的开口端称为栈顶
-
栈底:封口端称为栈底。
<2>操作
- 进栈:向栈中添加元素,此过程被称为"进栈"(入栈或压栈);
- 出栈:从栈中提取出指定元素,此过程被称为"出栈"(或弹栈)
(2)使用
栈一般来处理逆序和回退的相关处理。
(3)实现
<1>结构
栈是操作受限制的线性表,根据不同的存储结构可分成顺序栈和链式栈。
- 顺序栈:将顺序表的有效长度作为栈顶指针,在顺序表的末尾删除和插入节点。
- 链式栈:将链表的头结点作为栈顶指针,入栈采用头插法。
<2>操作
- 创建栈
- 入栈
- 出栈
- 获取栈顶元素
- 判空
6.队列
(1)队列是什么
<1>概念
队列是一种只能从表的一端存数据另一端取数据且遵循FIFO(先进先出)原则的线性存储结构。
- 队尾:在队列的一端只能插入元素,
- 队首:在队列的另一端只能删除元素。
<2>操作
- 入队:数据元素进队列的过程称为 "入队"
- 出队:出队列的过程称为 "出队"。
(2)使用
队列一般用来处理与等待相关的处理。
(3)实现
考虑到每次出队和入队都要移动队首和队尾指针。若采用顺序存储,将会有可能造成顺序表前段部分存储单元的浪费。虽说可以采用循环队列的方式复用存储单元,若遇到队列满的情况,将队列扩容比较麻烦。因此建议用链表的方式实现队列。
- 顺序队列:在index=0,入队,在index=size-1,为出队元素
- 链式队列:尾部入队,头部出队,尾插法。
<1>结构
链式队列 (技巧:使用哑元)
链式的head指向dummy,tail指向尾部,从尾部入队,从头部出队。(尾插法)
<2>函数
- 创建队列
- 入队
- 出队
- 获取队首元素
- 判空
(4)两个栈实现一个队列
思想:(两个栈各司其职)
- stack1作为队列的入口,stack2作为队列的出口;
- 入队列的操作就是入stack1;出队列操作:若stack2为空,则将stack1里面的数据入栈到stack2中,再出栈,如果stack2不为空则直接出栈。
(5)两个队列实现一个栈
思想:(空队列和非空队列的互捣)
- 两个队列que1和que2不管是插入还是弹出或者查看栈顶元素,总是要保证有一个队列为空。
- 入栈操作:总是往有数据的列队插入,默认两个列队空时,往que1插入
- 出栈操作:从非空队列中删除元素并插入到空队列中,直到非空队列剩下一个元素,改元素就是出栈的元素。
7.简单排序算法
(1)qsort
qsort包含在
<1>函数原型
void qsort(s,n,sizeof(s[0]),cmp);
- 参数
s:参与排序的数组名或者也可以理解成开始排序的地址;
n:参与排序的元素个数;
sizeof:单个元素的大小;
cmp:比较函数(回调函数)
<2>cmp函数
返回1:左边放在右边的后面;-1:左边的放在右边的前面。
int cmp(const void* a,const void* b){
int l=*(int*)a;
int r=*(int*)b;
if(l==r) return 0;
return l>r?1:-1;
}
<3>缺点
1、快排是不稳定的,这个不稳定一个表现在其使用的时间是不确定的,最好情况(O(n))和最坏情况(O(n^2))差距太大,我们一般说的O(nlog(n))都是指的是其平均时间。
-
2、部分排序:如果要对数组进行部分排序,比如对一个s[n]的数组排列其从s[i]开始的m个元素,只需要在第一个和第二个参数上进行一些修改:
void qsort(&s[i],m,sizeof(s[i]),cmp);
(2)冒泡排序
<1>原理
从第一个元素开始比较相邻的两个元素,如果左边的大于右边的,就交换这两个元素,大的往后移动,当右边大于左边就保持不变。所以每经过一次冒泡,就会找出最大的一个元素。当有n个元素时,第一次参与冒泡的元素是n个,比较n-1次;第二次参与冒泡的元素是n-1个(最大的元素不再需要排序),比较n-2次,总共需要n-1次冒泡。
<2>代码
void bubble_sort(int* arr,int n){
for(int i=0;i<3>复杂度分析
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:稳定的,排序过程中不改变相同元素的相对位置。
(3)选择排序
<1>原理
设定索引为0的元素是最大值max,其索引为maxindex,然后让max与index等于1...n-1的元素进行比较,找到max和maxindex,最后让max和最后一个元素进行交换,这样每次选择,就会找到当前元素的最大值。
<2>代码
void select_sort(int* arr,int n){
for(int i=0;imax){
max=arr[j];
maxindex=j;
}
}
arr[maxindex]=arr[n-i-1];//交换最大元素和最后一个元素
arr[n-i-1]=max;
}
}
<3>复杂度
时间复杂度:O(n^2)
空间复杂度:O(1)
不稳定。
(4)插入排序
打扑克。
<1>原理
- 只含有1个元素的序列必定是有序的;
- 第1轮:将第2个元素插入到由第1个元素组成的序列中,将其与第1个元素进行比较,如果第2个元素小于第1个元素,进行交换,此时前两个元素组成的序列完成排序。
- 第2轮:将第3个元素插入到由前两个元素组成的有序序列中,将第3个元素与有序序列的最后一个元素进行比较,如果需要发生交换,则将第三个元素替换成有序序列的最后一个元素,并保存之前的第三个元素,再将改元素与有序序列的倒数第二个进行比较,如果不需要交换,则停止,把保存的第三个元素填到有序序列的倒数第二个元素的位置。
- 第 i 轮,将第 i+1 个元素插入由前 i 个元素组成的子序列中,依次与第 i、i-1、……、1 个元素做比较,如果小于则交换位置。由于前 i 个元素都是有序的,因此一旦出现不大于第 i+1 个元素的数即可停止比较,比较次数 ≤ i,此时前 i+1 个元素组成的子序列完成排序。
<2>代码
void insert_sort(int* arr,int n){
for(int i=1;i=0;--j){
if(j>0 && arr[j-1]>tmp){
arr[j]=arr[j-1];
}else{
arr[j]=tmp;
break;//否则后面的元素都会变成tmp
}
}
}
}
}
<3>复杂度
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:稳定的,排序过程中不改变相同元素的相对位置。
8.递归(Recursion)
(1)概念
<1>定义
递归是一种直接或者间接调用自身函数。
<2>本质
把问题分解成规模缩小的同类问题的子问题。(递归就是函数的“套娃”)
<3>套路
关系+出口
- 确定递归公式
- 确定边界条件
<4>示例
- 打印1到10
法1:
void printN(int n){
if(n<0) return;
printN(n-1);
printf("&n=%p:n=%d\n",&n,n);//
}
法2:
int f(int n){
if(n==1) return 1;
else return f(n-1)+1;
}
int main(){
//printN(10);
for(int i=1;i<11;++i){
printf("%d ",f(i));
}
printf("\n");
}
- 1-n求和
关系:f(n)=f(n-1)+n
出口:f(1)=1
代码:
int sum(int n){
if(n==0) return 0;
else return sum(n-1)+n;
}
- 打印数组
void printN(int* arr,int n,int i){
if(i==n) return;
cout<< arr[i]<- 数组求和
int sumN(int* arr,int n,int i){//i是下标,表示从i开始求和
if(i==n-1) return arr[i];
else return arr[i]+sumN(arr,n,i+1);
}
int sumN(int* arr,int n){
return sumN(arr,n,0);
}
- 求数组的最大值
int maxarr(int* arr,int n,int i){
if(i==n-1) return arr[i];
else{
if(maxarr(arr,n,i+1)>arr[i]){
return maxarr(arr,n,i+1);
}else{
return arr[i];
}
}
}
- 斐波那契数列(*)
(1)兔子问题
//f(n)=f(n-1)+f(n-2)
//f(1)=1;f(2)=1
int Fibonacci(int n){
if(n==1 || n==2) return 1;
//递归
//return Fibonacci(n-1)+Fibonacci(n-2);
//迭代
int prev = 1;
int curr = 1;
for(int i=3;i<=n;++i){
int res = prev + curr;
prev = curr;
curr = res;
}
return curr;
}
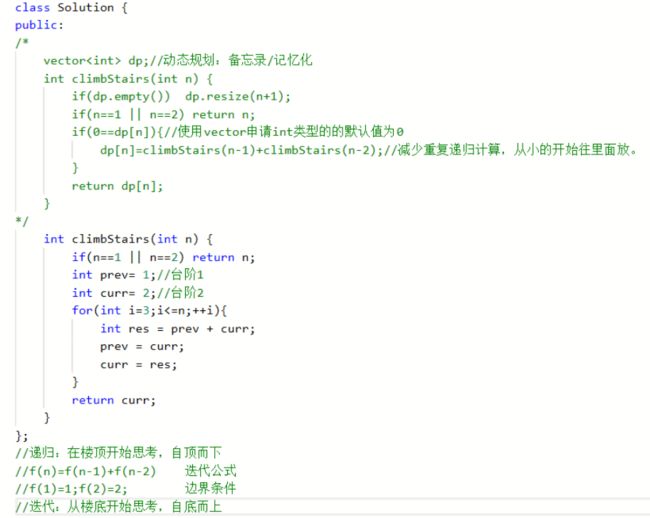
(2)爬楼梯
直接使用递归可能会超时!!需要用到动态规划。!!!
(2)递归的缺点
<1>空间
递归可能耗内存。(因为:函数参数中的每个变量都会重新申请内存)
可能导致吐核。
<2>时间
会很耗时(尤其对于两个或者三个函数相加的运算),主要原因是会重复计算某些值,会导致运行超时,解决:使用动态规划,申请动态数组来记录已经计算过的函数值。
动态规划:解决递归性能问题的一种方法。
动态规划讲解:https://leetcode-cn.com/problems/house-robber/solution/dong-tai-gui-hua-jie-ti-si-bu-zou-xiang-jie-cjavap/
可以使用time来统计执行时间。
time ./a.out
9.高级排序算法
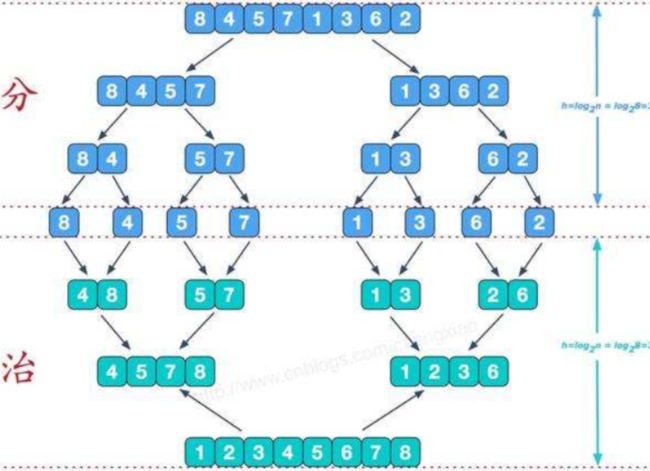
(1)归并排序
<1>原理
分到一定细度的时候,每一个部分就只有一个元素了,那么我们此时不用排序,对他们进行一次简单的归并就好了
<2>步骤
-
1.实现两个有序数组的合并(*)
void merge(int* arr,int n,int mid); -
2.拆分并合并数组(递归)
void merge_sort(int* arr,int n);
<3>代码
//归并排序
void merge(int*arr,int n,int mid) {
int temp[n];
int p=0;//前半部分下标
int q=mid;//后半部分下标
int k=0;//结果下标
while(p<4>复杂度
- 时间复杂度:一共拆分log2(n)次,每次比较n个元素,一共比较nlog2(n)次。
- 空间复杂度:需要增加额外空间n+log2(n)(临时数组n和递归调用函数栈log2(n)),空间复杂度为O(n)
- 稳定
(4)快速排序
<1>理解
以第一个个元素为基准,并且设置左右两个哨兵,右哨兵先走,当遇到比基准小的后,停止,然后左边的哨兵再走,当遇到比基准大的数停止,交换左右两个哨兵,然后再从右哨兵开始,重复,直到左右哨兵相遇为止。
<2>代码
- 递归
int partition(int* arr,int n){
int priot=arr[0];//以第一个元素为基准
int low=0;//从左往右
int height=n-1;//从右往左
while(low=priot) height--;
// 如果队尾元素小于tmp了,需要将其赋值给low
//arr[low]=arr[height];
// 当队首元素小于等于tmp时,向前挪动low指针
while(low - 非递归
递归的算法主要是在划分子区间,如果要非递归实现快排,只要使用一个栈来保存区间就可以了。
一般将递归程序改成非递归首先想到的就是使用栈,因为递归本身就是一个压栈的过程。
void quicksortnonrecursive(int* arr,int n){
stack s;
int low=0;
int height=n-1;
if(lowlow){
s.push(low);
s.push(pos-1);
}
if(pos+1start){
s.push(start);
s.push(mid-1);
}
if(mid+1 非递归的算法比递归实现还要慢。 因为递归算法使用的栈由程序自动产生,栈中包含:函数调用时的参数和函数中的局部变量。如果局部变量很多或者函数内部又调用了其他函数,则栈会很大。每次递归调用都要操作很大的栈,效率自然会下降。而对于非递归算法,每次循环使用自己预先创建的栈,因此不管程序复杂度如何,都不会影响程序效率。但是对于上面的快速排序,由于局部变量只有一个mid,栈很小,所以效率并不比非递归实现的低。
<3>复杂度
- 时间复杂度:一共拆分log2(n)次,每次比较n个元素,一共比较nlog2(n)次。
- 空间复杂度:需要增加额外空间log2(n)(递归调用函数栈log2(n)),空间复杂度为O(log2(n))
- 不稳定
(5)希尔排序(Shell排序)
希尔排序比插入排序的优势:
通过分组排序使元素逐渐靠近最终位置,从而减少了插入排序 时的移动次数。(先粗调再微调)
<1>理解
https://blog.csdn.net/qq_39207948/article/details/80006224
<2>代码
void ShellSort(int* arr,int len){
int temp,j;
for(int r=len/2;r>=1;r/=2){//间隔
//内层循环间距为r,分别比较对应元素,当r=1时,就是插入排序。
for(int i=r;i=0 && arr[j]>temp){
arr[j+r]=arr[j];
j -=r;
}
arr[j+r]=temp;
}
}
}