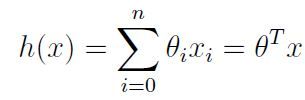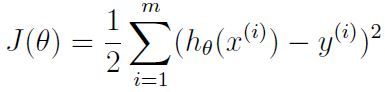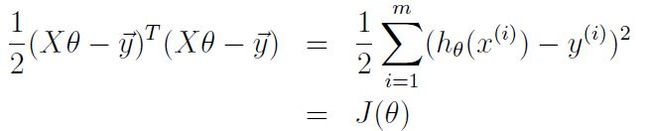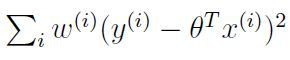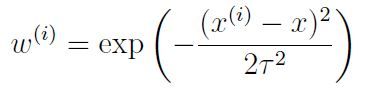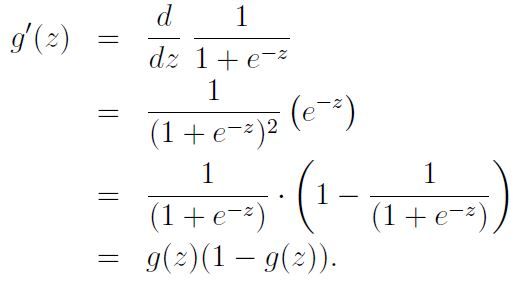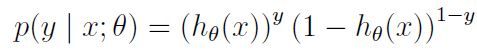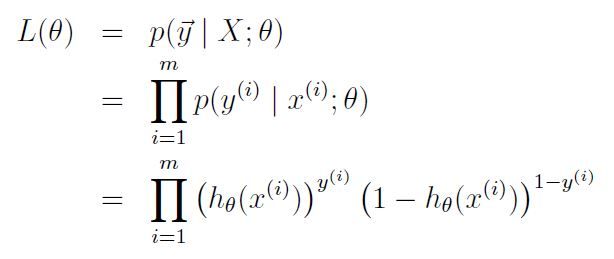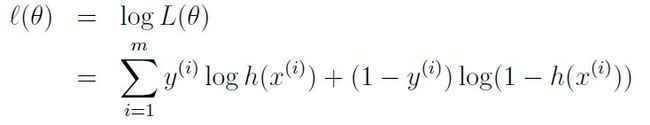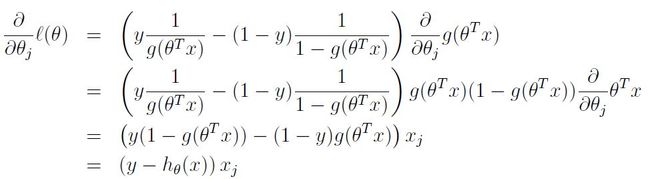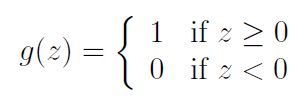最近发现脑子有点钝了，体重有点飘了，整个人有点颓废了，寻思写个记录一下学习内容吧，最近一直在看线性回归和逻辑回归，姑且把我学到的整理一下，预防老年痴呆。

以下内容是在看了吴恩达教授的CS229 之后自己整理出来的，估计有错，可能还TMD（战区导弹防御 Theater Missile Defense）有不少。

一. 线性回归

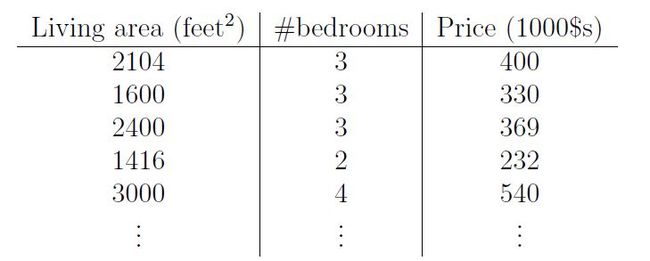
总说回归回归，到底做的是什么呢？个人理解，曲线拟合就可以算是一种线性回归，先简要概括一下note中用到的例子，老生常谈的房子估价问题，说是once upon a time不动产销售人员废了神劲调查到了一组房子的各项参数与售价，整理出来的表格如下：

参数1是房间面积（平方脚），参数2是卧室数量，随之对应房子的售价，当然对于其他问题而言可以加入更多参数，这里为了方便理解就用了一个相对简单的模型，课上教授用的例子是用polynomial来作为hypothesis function，还是那句话，具体问题具体分析，不同的模型需要不同的方程形式，用过matlab里cftool的同志可能有印象，拟合选项里有诸如一次函数，二次函数，多项式，傅里叶等等不同的拟合选项，得到的结果也是一母生 1001 子，连母 1010 个样，这个例子方程的具体形式如下：

我们的目的是找到最佳的 θ 来得到一个表现最好的方程，具体做法有梯度下降（GD），随机梯度下降（SGD），局部加权线性回归（Locally weighted linear regression）等等，保不齐哪天又整出个你没有玩过的船新版本算法了。

当大家面对一组数据时，我觉得不妨将自己的思维转变成向量思维，用向量的形式去看一组数，那么上述方程则可以写作：

接下来我们为了更加直接看到我们预测值与真实值的偏离程度，我们引入了一个至关重要的概念——COST FUNCTION

对于这道题教授说先用ordinary least square function 试试看，当然这不是唯一选择，对于不同问题我们也可以使用如交叉熵（cross entropy），absolute loss，log loss等等不同的函数，对症下药，这个函数形式如下：

好了，铺垫差不多结束，终于可以开始讲正题了。

梯度下降

刚开始接触这个知识时学长有一个问题三连直接把我噎死了，“谁的梯度下降，怎么降，为什么降”（虽然现在也在日常被噎。。。）

我们先来回顾一下一阶导数的意义，对于一个连续可导函数，一阶导数的正负确定了因变量随自变量的增加而上升或下降（连续不一定可导，可导必然连续。连续不一定可导，可导必然连续。连续不一定可导，可导必然连续。。。。）

连续不一定可导，可导必然连续

回过头看 cost function ，我们的目的不是没有蛀牙而是让预测值尽可能的靠近真实值（先不谈欠拟合过拟合问题），那么是不是就意味着cost function越小越好，在这个函数中自变量是 θ ，我们可以把这个问题用地理中的等高线模型来解释一下。

你的图不错，可惜下一秒就是我的了

我们可以把每一圈等高线看做一个J（θ）值，贫僧要做的不是“勇攀高峰”而是“下山还俗蹦迪”，代入一阶导数概念，如果为正，上山，那么相反，在原来位置减去使一阶导为正的自变量，是不是就go down了呢。

为了狗荡，我们需要求一下cost function对于参数 θ 的一阶偏导，具体过程如下：

根据上述结果，我们可以设置关于参数 θ 的update function了：

我们看到方程中有一个 α，这就是大名鼎鼎的 Learning Rate，它决定了每一步走多长，α值越大，迈的步子越长，当接近最低点时可能会来回爱的魔力转圈圈（晚期抖音PTSD患者），而α值越小，虽然能够更好得接近最优值但学习的越慢。

步子不能迈太大

至此，关于梯度下降的核心部分算是扯得差不多了，那么接下来讲讲具体做法吧。

批梯度下降（Batch Gradient Descent）

顾名思义，BGD的做法就是一批一批的来，可以从他的表达式看出其特点：

可以看出在迈出下一步之前，需要过一遍所有的sample，当数据规模小的时候还可以考虑一下，当数据规模庞大时如果还要全都放锅里焯一遍，计算成本太大，容易把硬件变成电磁炉。

所以人们就想能不能够找到一种新的做法来避免庞大计算量的出现，而且能够提高学习速度和精度呢？于是就有了

随机梯度下降（Stochastic Gradient Descent）

先看SGD的方程：

我们可以看到如果使用SGD，马上就可以获得学习进展，虽然寻找最优点的路线可能会相对曲折，而且在非常靠近最低点时可能会左右摇摆，但我们可以认为，在非常靠近最低点时，其周围的很小范围内所有值都可以看做是有效值，而且SGD从很大程度上减少了计算量，相比于BGD更加接近最低点，学习速度也更快。

对于上述的例子，我们可以用一个更直观的方法获得最佳参数。

正规化方程（Normal Equation）

个人感觉这个做法比之前两种更为直接，之前的算法需要一遍一遍的过，这位老哥可以直接出结果，用这个方法需要先知道几个符号概念和性质：

以及矩阵的迹（trace）相关知识，知道了这些我们回过头看一下cost function，将其写作vector的形式：

对其求关于参数 θ的偏导，吴教授在note中给出了运算过程，当然你也可以自己拿草纸自我纠缠一下：

根据求到的结果可以直接看到，理想情况是使偏导直接等于0，我们就可以找到极值点，因此可得关系式：

但是值得注意的是，虽然这种做法能够直接找到最优值，但由于它是基于矩阵运算，当数据规模增加后运算成本也会提高。

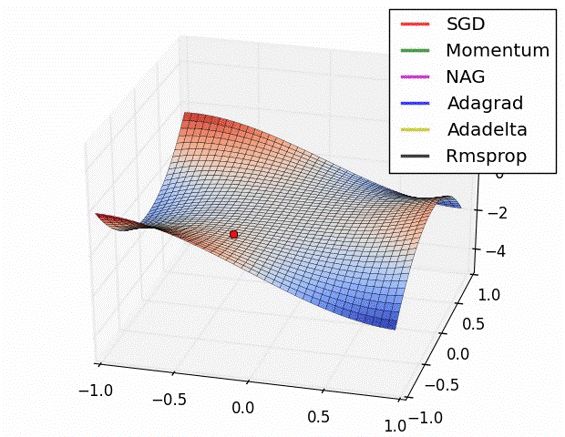
如何能够更快更好的下降一直是线性回归算法的研究方向之一，衍生出来的有例如 mini batch，momentum，AdaGrad，NAG等等，他们可以统称为优化器（optimizer），使用哪种还是要具体分析，不过最近发现Adam optimizer似乎烂大街了，是个人都用一下，再次不对各类optimizer做过多描述了，用的时候再说，各类optimizer的表现可以从下图看到：

第10080次尝试，似乎依然是静态，自己上网找吧，我不管了！

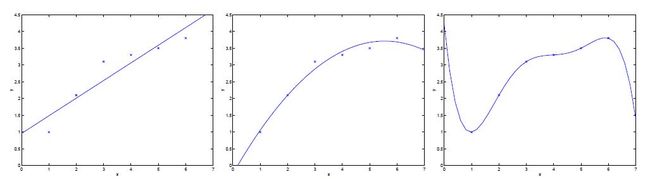
以上算法部分有一个共同的问题，都太过于追求曲线与数据的拟合程度，当θ数量比较少时这种现象可能不太明显，但假设一下training set若是有n个特征x，每个x都对应一个θ，曲线会经过所有点，这时候就会出现过拟合（overfitting）的情况，相反，若是 θ 过少，则会欠拟合（underfitting），如下图：

为了避免上述两种情况，首先讲一下

局部加权线性回归（Locally weighted linear regression）

简单来说，此种做法就是在cost function前加了一个weight项，使得其变为：

W的定义式为：

其中 τ 被称作带宽参数（bandwidth parameter）经过试验（自己回去编程自己看）可以看到如果此参数过小可能会存在过拟合，过大会存在欠拟合，所以需要通过反复试验来找到一个最佳值。

另外有其他解决拟合问题的做法

1.针对于想要研究的问题选择恰当的模型，如上文所说的在matlab cftool里的拟合选项那样。

2.正则化（regularization）在更新方程中加入正则项，例如L1正则，L2正则，具体特性可以查一下，简单说L1正则就是使得靠近0的参数趋近0，从而给一部分参数打个响指（紫薯精警告），L2正则则是会在越接近0时梯度越小，从而降低模型复杂度。

3.数据集扩增（data augmentation），顾名思义，多整点儿有用的数据呗，5个不行就500个，再不行切四瓣，在看不出特性就掉个个儿，还不够就加随机噪声，总有办法获取到大量有用的数据集。

4.删除结点个数（drop out），再开始学习前可以把网络中隐藏层（hidden layer）里的的一些结点随机删除，下一次之前换着删一波，这样也可以防止过拟合。

5.Early stopping，按照知乎上一位同志说的，一般做法是在训练时记录下最佳精度，当比如说10个，20个epoch都没能突破这个精度，此时认为啊这就是最佳精度了，就可以停止训练。

And so on，以上差不多就是我目前学习到的关于线性回归的知识了。

接下来是

逻辑回归（Logistic Regression）

目前来说逻辑回归经常被用来做分类问题，此时不能再用线性思维去解决非线性问题了，所以我们的预测方程需要变为：

这个形式可能还看不太出是啥，换一个形式：

这个方程称作逻辑函数（logistic function）或者别名：sigmoid function，对，就是激活函数（activation function）大军里的那个sigmoid，其图像如下：

这个函数有个神奇的性质就是他的一阶导：

因为逻辑回归说白了是个概率问题吗，假设只有两种标签0,1，我们可以写出概率的表达式：

假设训练集m个，我们可以写出这个问题的似然函数（likelihood function）：

说到似然函数第一个想到的跟苍蝇一样来回在眼前晃悠的四个字“最大似然”（Maximum Likelihood），顾名思义，对于此方程我们的目标是找到最大值，值越大证明我们预测的越准，举个栗子，我写了个方程来鉴定康师傅是不是个研究生，真实情况是他100%是个研究生（而且快要成shuttle王八了），刚开始算只是50%，我得想个办法至少把这个值提到百分之80,90吧。

不过在开始最大化之前，为了方便计算，先要对这个方程取个 log：