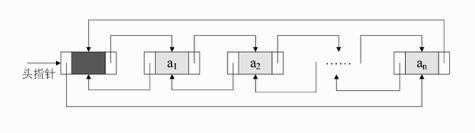
线性表
“线性表(List):零个或多个数据元素的有限序列。”
线性表的顺序存储结构
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。
线性表(a1,a2,......,an)的顺序存储示意图如下:
线性表的顺序存储结构的优缺点
- 优点:
尾插效率高,支持随机访问。 - 缺点:
中间插入或者删除效率低。 - 应用:
- 数组
- ArrayList
重要接口
构造方法()
add()
remove()
顺序存储结构的插入
- 插入算法的思路:
如果插入位置不合理,抛出异常;
如果线性表长度大于等于数组长度,则抛出异常或动态增加容量;
从最后一个元素开始向前遍历到第i个位置,分别将它们都向后移动一个位置;
将要插入元素填入位置i处; ?表长加1。
实现代码如下:
/* 初始条件:顺序线性表L已存在,1≤i≤
ListLength(L), */
/* 操作结果:在L中第i个位置之前插入新的数据元
素e,L的长度加1 */
Status ListInsert(SqList *L, int i, ElemType e)
{
int k;
/* 顺序线性表已经满 */
if (L->length == MAXSIZE)
return ERROR;
/* 当i不在范围内时 */
if (i < 1 || i >L->length + 1)
return ERROR;
/* 若插入数据位置不在表尾 */”
if (i <= L->length)
{
/*将要插入位置后数据元素向后移动一位 */
for (k = L->length - 1; k >= i - 1; k--)
L->data[k + 1] = L->data[k];
}
/* 将新元素插入 */
L->data[i - 1] = e;
L->length++;
return OK;
}
顺序存储结构的删除
- 删除算法的思路:
如果删除位置不合理,抛出异常;
取出删除元素;
从删除元素位置开始遍历到最后一个元素位置,分别将它们都向前移动一个位置;
表长减1。
实现代码如下:
/* 初始条件:顺序线性表L已存在,1≤i≤
ListLength(L) */
/* 操作结果:删除L的第i个数据元素,并用e返回
其值,L的长度减1 */
Status ListDelete(SqList *L, int i, ElemType *e)
{
int k;
/* 线性表为空 */
if (L->length == 0)
return ERROR;
/* 删除位置不正确 */
if (i < 1 || i > L->length)
return ERROR;
*e = L->data[i - 1];
/* 如果删除不是最后位置 */
if (i < L->length)
{
/* 将删除位置后继元素前移 */
for (k = i; k < L->length; k++)
L->data[k - 1] = L->data[k];
}
L->length--;
return OK;
}
线性表的链式存储结构
线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的。这就意味着,这些数据元素可以存在内存未被占用的任意位置
除了存储其本身的信息之外,还需存储一个指示其直接后继的信息(即直接后继的存储位置)。我们把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。指针域中存储的信息称做指针或链。这两部分信息组成数据元素ai的存储映像,称为结点(Node)。
n个结点(ai的存储映像)链结成一个链表,即为线性表(a1,a2,...,an)的链式存储结构,因为此链表的每个结点中只包含一个指针域,所以叫做单链表。单链
表正是通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起,
-头指针与头结点的异同
链表的学习通过简单的自定义LinkedList来学习记录下
public class LinkedList {
/**
* 结点
*/
private static class Node {
E item;
Node prev;
Node next;
public Node(Node prev, E item, Node next) {
this.item = item;
this.prev = prev;
this.next = next;
}
}
public LinkedList() {
}
//头节点
Node first;
//尾节点
Node last;
//大小
int size;
/**
* 添加数据在最后
*/
public void add(E e) {
linkLast(e);
}
/**
* 添加到最后
* @param e
*/
private void linkLast(E e) {
Node newNode = new Node(last, e, null);
Node l = last;
last=newNode;
if(l==null){
first=newNode;
}else {
l.next = newNode;
}
size++;
}
/**
* 查找位置
*/
public E get(int index){
if(index<0 || index>size){
return null;
}
return node(index).item;
}
/**
* 获取index位置上的节点
*/
private Node node(int index){
//如果index在整个链表的前半部分
if(index<(size>>1)){ //1000 100 10
Node node=first;
for (int i = 0; i < index; i++) {
node=node.next;
}
return node;
}else{
Node node=last;
for (int i = size-1; i > index; i--) {
node=node.prev;
}
return node;
}
}
/**
* 添加数据在index位置
*/
public void add(int index,E e) {
if(index<0 || index>size){
return ;
}
if(index==size){
linkLast(e);
}else{
Node target=node(index);// index=2
Node pre=target.prev;
Node newNode=new Node(pre,e,target);
if(pre==null){
first=newNode;
target.prev = newNode;//4
}else {
pre.next = newNode;//3
target.prev = newNode;//4
}
size++;
}
}
/**
* 删除元素
*/
public void remove(int index){
Node target=node(index);
unlinkNode(target);
}
private void unlinkNode(Node p) {//index=2
Node pre=p.prev;
Node next=p.next;
if(pre==null){
first=p.next;
}else{
pre.next=p.next;
}
if(next==null){
last=p.prev;
}else{
next.prev=p.prev;
}
size--;
}
}
双向链表(double linkedlist)
双向链表(double linkedlist)是在单链表的每个结点中,再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域,一个指向直接后继,另一个指向直接前驱。
既然单链表也可以有循环链表,那么双向链表当然也可以是循环表。
双向链表的循环带头结点的空链表如图
可参考
-
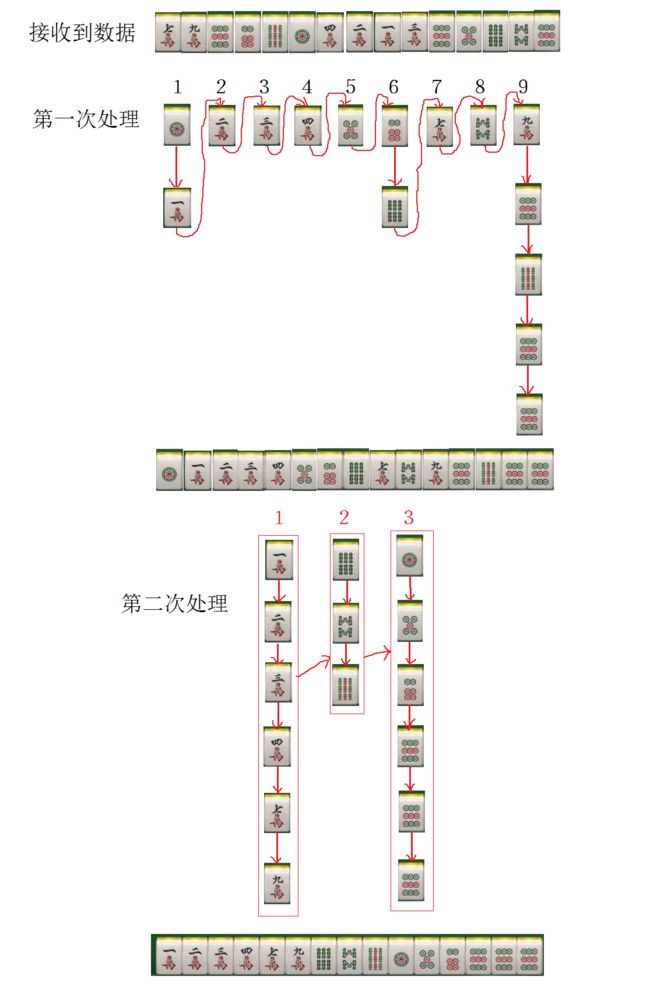
链式基数排序
基数排序是采用“分配”与“收集”的办法,用对多关键码进行排序的思想实现对单关键码进行排序的方法
麻将实体类:
public class Mahjong {
public int suit;//筒,万,索
public int rank;//点数 一 二 三
public Mahjong(int suit, int rank) {
this.suit = suit;
this.rank = rank;
}
@Override
public String toString() {
return "("+this.suit+" "+this.rank+")";
}
}
实现类:
public class ExampleUnitTest {
@Test
public void addition_isCorrect() throws Exception {
LinkedList list=new LinkedList();
list.add(new Mahjong(3,1));
list.add(new Mahjong(2,3));
list.add(new Mahjong(3,7));
list.add(new Mahjong(1,1));
list.add(new Mahjong(3,8));
list.add(new Mahjong(2,2));
list.add(new Mahjong(3,2));
list.add(new Mahjong(1,3));
list.add(new Mahjong(3,9));
System.out.println(list);
radixSort(list);
System.out.println(list);
}
public static void radixSort(LinkedList list){
//先对点数进行分组
LinkedList[] rankList=new LinkedList[9];
for (int i = 0; i < rankList.length; i++) {
rankList[i]=new LinkedList();
}
//把数据一个个放到对应的组中
while(list.size()>0){
//取一个
Mahjong m=list.remove();
//放到组中 下标=点数减1的
rankList[m.rank-1].add(m);
}
//把9组合并在一起
for (int i = 0; i < rankList.length; i++) {
list.addAll(rankList[i]);
}
//先花色进行分组
LinkedList[] suitList=new LinkedList[3];
for (int i = 0; i < suitList.length; i++) {
suitList[i]=new LinkedList();
}
//把数据一个个放到对应的组中
while(list.size()>0){
//取一个
Mahjong m=list.remove();
//放到组中 下标=点数减1的
suitList[m.suit-1].add(m);
}
//把3个组合到一起
for (int i = 0; i < suitList.length; i++) {
list.addAll(suitList[i]);
}
}
}
总结
- 蛮力法
蛮力法(brute force method,也称为穷举法或枚举法)
是一种简单直接地解决问题的方法,
常常直接基于问题的描述,
所以,蛮力法也是最容易应用的方法。
但是,用蛮力法设计的算法时间特性往往也是最低的,
典型的指数时间算法一般都是通过蛮力搜索而得到的 。(即输入资料的数量依线性成长,所花的时间将会以指数成长)冒泡排序
public static void bubbleSort(Cards[] array){ //3-5个数据 78
//1 2 3 4 5 9 4 6 7 n*(n-1)/2 n
for(int i=array.length-1;i>0;i--) {
boolean flag=true;
for (int j = 0; j < i; j++) {
if (array[j].compareTo(array[j+1])>0) {
Cards temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
flag=false;
}
}
if(flag){
break;
}
}
}
应用:数据量足够小,比如斗牛游戏的牌面排序
- 选择排序
public static void selectSort(int[] array){
for(int i=0;i- 快速排序的基础
来源百度百科:
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序是面试出现的可能性比较高的,也是经常会用到的一种排序,应该重点掌握。
一、第一趟快速排序
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小
百度百科的话并没有说到重点,更简单的理解是这样的:在数组中找一个支点(任意),经过一趟排序后,支点左边的数都要比支点小,支点右边的数都要比支点大!
现在我们有一个数组:int arr[]={1,4,5,67,2,7,8,6,9,44};
经过一趟排序之后,如果我选择数组中间的数作为支点:7(任意的),那么第一趟排序后的结果是这样的:{1,4,5,6,2,7,8,67,9,44}
那么就实现了支点左边的数比支点小,支点右边的数比支点大
二、递归分析与代码实现
现在我们的数组是这样的:{1,4,5,6,2,7,8,67,9,44},既然我们比7小的在左边,比7大的在右边,那么我们只要将”左边“的排好顺序,又将”右边“的排好序,那整个数组是不是就有序了?想一想,是不是?
又回顾一下递归:”左边“的排好顺序,”右边“的排好序,跟我们第一趟排序的做法是不是一致的?
只不过是参数不一样:第一趟排序是任选了一个支点,比支点小的在左边,比支点大的在右边。那么,我们想要”左边“的排好顺序,只要在”左边“部分找一个支点,比支点小的在左边,比支点大的在右边。
..............
在数组中使用递归依照我的惯性,往往定义两个变量:L和R,L指向第一个数组元素,R指向在最后一个数组元素
递归出口也很容易找到:如果数组只有一个元素时,那么就不用排序了
所以,我们可以写出这样的代码:
* 快速排序
*
* @param arr
* @param L 指向数组第一个元素
* @param R 指向数组最后一个元素
*/
public static void quickSort(int[] arr, int L, int R) {
int i = L;
int j = R;
//支点
int pivot = arr[(L + R) / 2];
//左右两端进行扫描,只要两端还没有交替,就一直扫描
while (i <= j) {
//寻找直到比支点大的数
while (pivot > arr[i])
i++;
//寻找直到比支点小的数
while (pivot < arr[j])
j--;
//此时已经分别找到了比支点小的数(右边)、比支点大的数(左边),它们进行交换
if (i <= j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
//上面一个while保证了第一趟排序支点的左边比支点小,支点的右边比支点大了。
//“左边”再做排序,直到左边剩下一个数(递归出口)
if (L < j)
quickSort(arr, L, j);
//“右边”再做排序,直到右边剩下一个数(递归出口)
if (i < R)
quickSort(arr, i, R);
}
摘抄 公众号(微信搜Java3y)文章
摘录来自: 程杰. “大话数据结构。” Apple Books.