Ragged tensor,即参差不齐的张量,用于记录长度不规则的数据。
例如,句子的语气分类任务中,不同句子的长度长短不一,却被保存在同一个数据集中,这时,就不能用张量去保存这句子了,就要用到Ragged tensor。
原生的python list实际上是支持类似的功能的,无非就是一个list,里面装了很多子list,这些子list的长度又不一样。
例如:
ragged_list = [[1],[2,3]]
这种写法是完全不会报错的。
当然,这种东西显然无法转化为numpy中的array。也就是说,在偏向矩阵运算的包中,不支持这种非规则矩阵数据的做法是十分常见的。
然而,tensorflow 2.0还是毅然决然地对这类数据进行了支持。这就是 Ragged tensor,例如要把上面的那个数据转化为Ragged tensor,只需要:
import tensorflow as tf
rt = tf.ragged.constant([[1],[2,3]])
虽然以最直白的方式介绍完这个Ragged tensor,就会觉得这玩意儿,也“不过如此”。但仔细想想这个东西还是极富想象力的。例如上面说的可以很好地对句子进行表示,而不是添加一系列烦人的padding。最关键的是,像RNN这种,本身就可以支持变长序列的神经网络,只因为之前的tensorflow 1.0 的tensor所表示的序列都必须是定长的,就导致我们必须间接地去实现RNN的对变长序列进行处理的能力。
而在tensorflow 2.0 中,你不仅可以使用Ragged tensor对你的变长序列数据进行最直白的记录,还可以利用封装好的“tf.keras.layers.LSTM”直接对包含变长序列的batch进行处理。
回到本文最初想介绍的ragged rank
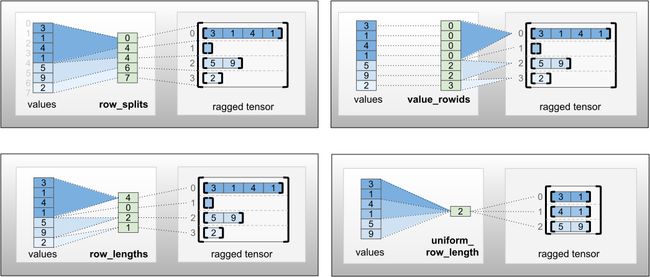
要解释ragged rank,首先就要介绍Ragged tensor在实现的底层的实现方式。事实上,Ragged tensor有两部分构成,一是一维的数组记录了所有的数据,二是一个表示归属的数组来表示每个数属于哪一行。(这其实是一种为了便于理解所采用的十分不精确的表述)。
我们来盗个图:
看右上角的图,[3,1,4,1,5,9,2]就是刚才说的那个记录所有实际数据的一维数组,我们后面称之为数据数组。[0,0,0,0,2,2,3]分别表示每一个数字属于第几行,我们称之为归属数组。可以发现,数据数组和归属数组是一一对应的。
例如归属数组的第一个数,0,表示对应的数据数组中的3属于第一行,同理,3,1,4,1都属于第一眼,因此所表示Ragged tensor的第一行就是[3,1,4,1]。二三四行同理。
现在不仅解释了上面黑体的那句话,还解释了那句话为什么不严谨。
首先,表示归属的方式不止一种,而是由如图所示的四种(大同小异)。其次,表示数据的不仅可以是个向量,还可以是个矩阵甚至张量。
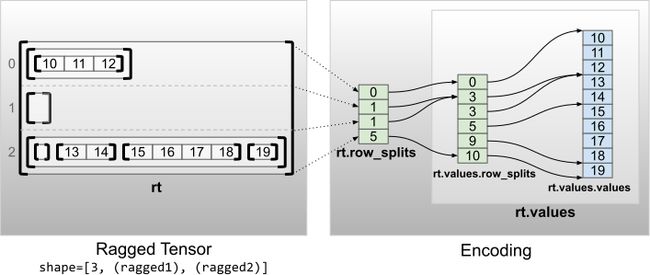
那如果一个三维的Ragged tensor,该如何表示呢?
再盗个图,
如图所示,这里整了一个两层的归属向量,结果就是把一个一维的向量,变成了一个三维的Ragged tensor。
讲到这里,就可以引出我们的ragged rank了。
通俗地讲,Ragged tensor的ragged rank就是指它所包含归属向量的层数。
我们第一次举的例子,归属向量只有一层,所以ragged rank就是1。而在三维的Ragged tensor中,由于采用了两层的归属向量,因此这里的ragged rank就是2。
我们再来看,另一种表示三维Ragged tensor的方式,
盗图:
在这个例子中,数据向量实际上是一个数据矩阵,然后利用一层的归属向量,得到了三维的Ragged tensor。那这里的ragged rank是多少呢?
因为这里的归属向量只有一层,因此,ragged rank竟然是1。
因此,一个Ragged tensor的ragged rank和它的维度并无直接关系,而是与其底层的实现方式直接相关。
查询一个Ragged tensor的ragged rank的方法?
上代码
rt = tf.RaggedTensor.from_row_splits(
values=[[1, 3], [0, 0], [1, 3], [5, 3], [3, 3], [1, 2]],
row_splits=[0, 3, 4, 6])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of partitioned dimensions: {}".format(rt.ragged_rank))
或者
tf.type_spec_from_value(rt)
所返回元组的倒数第二个数,就是rt的ragged_rank。
本文最有意思的部分:有没有可能,同样的一个Ragged tensor,由于底层实现不一样,导致它们对应的ragged_rank不一样?
亲测,答案是,有可能。
例子:
rt = tf.ragged.constant([[[1]],[[1],[1]]])
rt2 = tf.RaggedTensor.from_tensor(np.array([[[1],[1]],[[1],[1]]]), lengths=[1,2])
如果对二者进行打印,则都会得到:
但如果查看二者的ragged_rank,会发现,rt的是2,而rt2的则是1:
怎么样,是不是挺有意思的?