此文仅记录学习树相关的知识以及实现逻辑和代码片段。包含二叉树,二叉查找树,平衡二叉查找树(AVL树,红黑树),均已es6语法实现。查阅前默认你已经具备树相关的的基本概念,如果对某个部分感兴趣建议直接跳转到相应部分,have fun!
(图太难画了,有空补,逃 ~)
所有完整代码:Code
树的基本概念
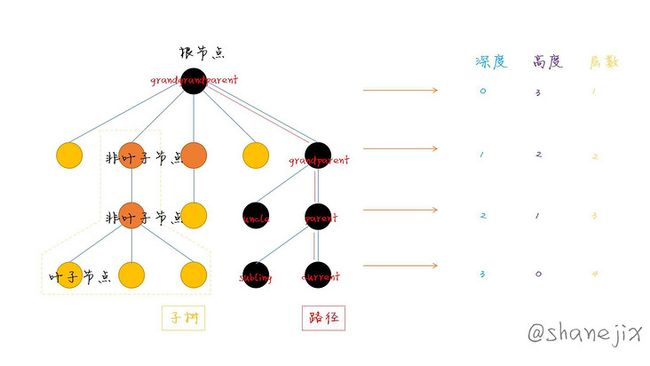
一图胜千言,下图是一棵多叉树:
树的概念类似生活中树的树根,一生二,二...,这样子。类比月现实中的树根不会错综交织成网状,树的概念也一样。如果树的分叉相互连结,那就脱离树的范畴。如下列举后续会用到的一些概念:
节点,度 :一个实心圆就是一个节点,向下分叉的个数就是节点的度(degree)。黑色节点表示了节点节点间的层次关系,树的旋转等操作会用到这些关系,比较重要。节点按度的个数又可以分为,叶子节点(度为0),非叶子节点(度不为零),当然一个节点的度就是该节点的一颗子树。
深度,高度,层数:这三个概念比较容易混淆,放在一起类比。深度,类比于树根从地表向下衍生的深度。高度,类比于楼房的地表绝对高度或者山峰的海拔高度。可能你也发现了,首先有一个参考标准,相对于谁的高度或深度。所以一般会计算整棵树的高度(深度),或者某个节点的高度(深度)。然后,就是计数的规则,一般情况,高度,深度都是从0开始计数,层次从1开始计数。但是,也有从层次从0计数,高度,深度从1计数的时候。
二叉树
各种二叉树:
二叉树的特点
最大度为2 :各个节点的度最大为2,最多有两颗子树有序树:左右子树严格有顺,即使左子树,右子树为空二叉树的性质
非空二叉树的第 k(k>=1) 层最多有 2^(k-1) 个节点在高为 h(h>=1)的二叉树中最多有 2^h -1 个节点非空二叉树中,如果度为零的节点个数为 n0 ,度为 1 的节点个数为 n1 ,度为 2 的节点个数为 n2 ,则:n0 = n2 + 1常见二叉树
真二叉树(full binary tree):所有节点的度都为0或2
满二叉树(perfect binary tree):最后一层节点的度都为0,其他节点的度都为2
完全二叉树(complete binary tree):根节点到倒数第二层,是满二叉树,最后一层的叶子节点靠左对齐
完全二叉树的性质
度为1的节点只有左子树,并且要么为1要么为0满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树节点相同的二叉树,完全二叉树的高度最小 假设完全二叉树高度为 h (h>=1),那么至少有 2^(h -1) 个节点,至多有 2^h - 1 个节点;
若总结点数为 n , 则 2^(h-1) < n < 2^h - 1二叉树的遍历
访问二叉树中的各个节点,一般是左右子树的访问顺序是先左子树,然后右子树;当然也可以先右子树后左子树,但是这就不是不是我们所熟知的前中后序遍历了。
前序遍历
遍历当前节点 -> 遍历当前节点的左子树 -> 遍历当前的节点的右子树BinaryTree.prototype.preorderTraversal = function (node, printer) {
if (node === null) return;
printer ? printer(node.value) : this.printer(node.value);
this.preorderTraversal(node.left, printer);
this.preorderTraversal(node.right, printer);
};中序遍历
遍历当前节点的左子树 -> 遍历当前节点 -> 遍历当前的节点的右子树BinaryTree.prototype.inorderTraversal = function (node, printer) {
if (node === null) return;
printer ? printer(node.value) : this.inorderTraversal(node.left);
this.printer(node.value, printer);
this.inorderTraversal(node.right, printer);
};后续遍历
遍历当前节点的左子树 -> 遍历当前的节点的右子树 -> 遍历当前节点BinaryTree.prototype.postorderTraversal = function (node, printer) {
if (node === null) return;
this.postorderTraversal(node.left, printer);
this.postorderTraversal(node.right, printer);
printer ? printer(node.value) : this.printer(node.value);
};层次遍历
从上到下,从坐到右,按层依次遍历二叉树BinaryTree.prototype.levelOrderTraversal = function (node, printer) {
if (node === null) return;
const queue = [];
queue.push(node);
while (queue.length) {
const currNode = queue.shift();
printer ? printer(node.value) : this.printer(currNode.value);
if (currNode.left) {
queue.push(currNode.left);
}
if (currNode.right) {
queue.push(currNode.right);
}
}
};二叉树搜索树
二叉搜索树,又名二叉排序树,二叉查找树,故名思意可以极大的提高查找效率
特征:
任意一个节点的值,都大于左子树中所有节点的值,都小于右子树中所有节点的值
二叉搜索树中节点存储的值必须具备可比较性实现二叉搜索树
接口设计:
export default class BinarySearchTreeNode extends BinaryTreeNode {
/**
* @param {*} value
* @param {function} compareFunction
* @return {*}
*/
constructor(value, compareFunction) {
super(value, compareFunction);
this.compareFunction = compareFunction;
}
/**
* @param {*} value
* @return {BinarySearchTreeNode}
*/
insert(value) {}
/**
* @param {*} value
* @return {boolean}
*/
find(value) {}
/**
* @param {*} value
* @return {boolean | Error}
*/
remove(value) {}
/**
* @param {*} value
* @return {boolean}
*/
contains(value) {}
/**
* @return {BinarySearchTreeNode}
*/
findMin() {}
}
允许传入自定义的比较器
插入:
- 树为空,插入root节点
- 树为不为空,找到父节点,插入父节点的左边 or 右边/**
* @param {*} value
* @return {BinarySearchTreeNode}
*/
insert(value) {
// curr.node.value === null
if (this.nodeValueComparator.equal(this.value, null)) {
this.value = value;
return this;
}
// curr.node.value < value
if (this.nodeValueComparator.lessThan(this.value, value)) {
// curr.node !== null
if (this.right) {
return this.right.insert(value);
}
// curr.node.right === null
const newNode = new BinarySearchTreeNode(value, this.compareFunction);
this.setRight(newNode);
return newNode;
}
// curr.node.value > value
if (this.nodeValueComparator.greaterThan(this.value, value)) {
// curr.node.left !== null
if (this.left) {
return this.left.insert(value);
}
// curr.node.left === null
const newNode = new BinarySearchTreeNode(value, this.compareFunction);
this.setLeft(newNode);
return newNode;
}
// curr.node.value === value
return this;
}删除:
- 删除的是叶子节点
-> 找到父节点,将父节点的左子树 or 右子树 设为null
-> 如果没有父节点,则是根节点,将root设置为null
- 删除的是度为1的节点
-> 找到父节点,用子树替代当前位置
-> 如果没有父节点,则是根节点,将root指向子树
- 删除的是度为2的节点
-> 找到父节点,找到前驱或者后继节点,替代当前节点,然后删除前驱或后继
-> 如果没有父节点,则是根节点,特殊处理
- 以上删除的节点可能是根节点
/**
* @param {*} value
* @return {boolean | Error}
*/
remove(value) {
const nodeToRemove = this.find(value)
if (!nodeToRemove) {
throw new Error('item not exit in this tree')
}
const parent = nodeToRemove.parent;
// degree === 0 node is a leaf and has no child
if (!nodeToRemove.left && !nodeToRemove.right) {
if (parent) {
parent.removeChild(nodeToRemove)
} else {
nodeToRemove.setValue(null)
}
}
// degree === 2 has tew children
else if (nodeToRemove.left && nodeToRemove.right) {
const nextBiggerNode = nodeToRemove.right.findMin();
if (!this.nodeComparator.equal(nextBiggerNode, nodeToRemove.right)) {
this.remove(nextBiggerNode.value);
nodeToRemove.setValue(nextBiggerNode.value)
} else {
nodeToRemove.setValue(nodeToRemove.right.value);
nodeToRemove.setRight(nodeToRemove.right.right);
}
}
// degree === 1 has only one child
else {
const childNode = nodeToRemove.left || nodeToRemove.right;
if (parent) {
parent.replaceChild(nodeToRemove, childNode)
// childNode.parent = parent
} else {
BinaryTreeNode.coypNode(childNode, nodeToRemove)
}
}
nodeToRemove.parent = null;
return true;
}前驱或后继是指中序遍历中当前节点的前一个或后一个节点其他接口相对容易,不再概述
平衡二叉搜索树
二叉搜索树在极端情况下添加和删除会退化为链表。
如何平衡二叉搜索树呢?只有在添加或删除后想办法降低树的高度。
下面一起看看AVL树和红黑树是如何实现的。
AVL树
引入平衡因子(balance factor) :某个节点的左右子树的高度差
特点:
每个节点的平衡因子只能是:1 0 -1;绝对值超过1则失衡实现AVL树
接口设计:
export default class AvlTree extends BinarySearchTree {
/**
* @param {*} value
*/
insert(value) { }
/**
* @param {*} value
*/
remove(value) {}
/**
* @param {BinarySearchTreeNode} node
*/
balance(node) {}
/**
* @param {BinarySearchTreeNode} rootNode
*/
rotateLeftLeft(rootNode) {}
/**
* @param {BinarySearchTreeNode} rootNode
*/
rotateLeftRight(rootNode) {}
/**
* @param {BinarySearchTreeNode} rootNode
*/
rotateRightRight(rootNode) { }
/**
* @param {BinarySearchTreeNode} rootNode
*/
rotateRightLeft(rootNode) {}
}添加:
- 当前节点不会失衡,父节点,祖先节点可能会失衡
- 失衡会像上逐级传播insert
/**
* @param {*} value
*/
insert(value) {
// BinarySearchTree.insert
super.insert(value);
// move up from current node to root to check balance factors
let currentNode = this.root.find(value);
while (currentNode) {
this.balance(currentNode);
currentNode = currentNode.parent;
}
}平衡
通过平衡因子判断节点插入位置的情况balance
/**
* @param {BinarySearchTreeNode} node
*/
balance(node) {
// balance factor is not ok
if (node.balanceFactor > 1) {
// left rotate
if (node.left.balanceFactor > 0) {
// left-left rotate
this.rotateLeftLeft(node);
} else if (node.left.balanceFactor < 0) {
// left-right rotate
this.rotateLeftRight(node);
}
} else if (node.balanceFactor < -1) {
// right rotate
if (node.right.balanceFactor < 0) {
// right-right rotate
this.rotateRightRight(node);
} else if (node.right.balanceFactor > 0) {
// right-left rotate
this.rotateRightLeft(node);
}
}
}通过层次和有序判断节点插入位置的情况balance2
/**
* @param {*} grand
* @returns {*}
*/
balance2(grand) {
const parent = grand.tallerChild();
const child = parent.tallerChild();
if (parent.isLeftChild(grand)) {
// left
if (child.isLeftChild(parent)) {
// left-left
rotateRight(grand);
} else {
// left-right
rotateLeft(parent);
rotateRight(grand);
}
} else {
// right
if (child.isRightChild(parent)) {
// right-right
rotateLeft(grand);
} else {
// right-left
rotateRight(parent);
rotateLeft(grand);
}
}
}通过层次和有序判断节点插入位置,4种情况统一处理balance3
/**
* @param {*} grand
* @returns {*}
*/
balance3(grand) {
const parent = grand.tallerChild();
const child = parent.tallerChild();
if (parent.isLeftChild(grand)) {
// left
if (child.isLeftChild(parent)) {
// left-left
rotate(grand, node, node.right, parent, parent.right, grand);
} else {
// left-right
rotate(grand, parent, node.left, node, node.right, grand);
}
} else {
// right
if (child.isRightChild(parent)) {
// right-right
rotate(grand, grand, parent.left, parent, node.left, node);
} else {
// right-left
rotate(grand, grand, node.left, node, node.right, parent);
}
}
}1. grandparent.left = parent.right
2. parent.parent = grandparent.parent
3. parent.right = grandparent
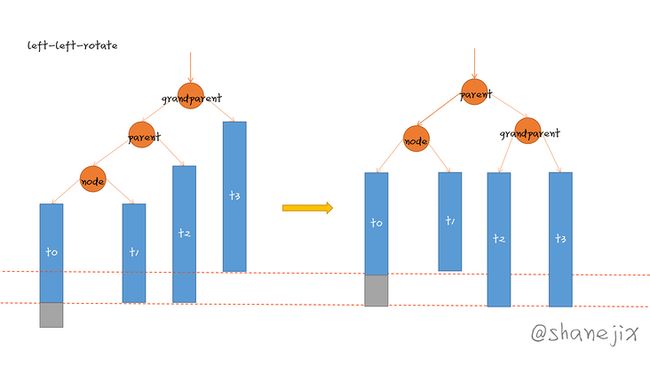
- 第1步和第2步可以交换rotateLeftLeft
/**
* @param {BinarySearchTreeNode} rootNode
*/
rotateLeftLeft(rootNode) {
const leftNode = rootNode.left;
rootNode.setLeft(null);
if (rootNode.parent) {
rootNode.parent.setLeft(leftNode);
} else if (rootNode === this.root) {
this.root = leftNode;
}
if (leftNode.right) {
rootNode.setLeft(leftNode.right);
}
leftNode.setRight(rootNode);
}left-right-左旋-右旋-双旋
1.先对parent节点左旋,变化为rotateLeftLeft情形
2.处理rotateLeftLeft情形rotateLeftRight
/**
*
* @param {BinarySearchTreeNode} rootNode
*/
rotateLeftRight(rootNode) {
const leftNode = rootNode.left;
rootNode.setLeft(null);
const leftRightNode = leftNode.right;
leftNode.setRight(null);
if (leftRightNode.left) {
leftNode.setRight(leftRightNode.left);
leftRightNode.setLeft(null);
}
rootNode.setLeft(leftRightNode);
leftRightNode.setLeft(leftNode);
this.rotateLeftLeft(rootNode);
}right-right-左旋-单旋
1. grandparent.right = parent.left
2. parent.parent = grandparent.parent
3. parent.left = grandparent
- 第1步和第2步可以交换rotateRightRight
/**
* @param {BinarySearchTreeNode} rootNode
*/
rotateRightRight(rootNode) {
const rightNode = rootNode.right;
rootNode.setRight(null);
if (rootNode.parent) {
rootNode.parent.setRight(rightNode);
} else if (rootNode === this.root) {
this.root = rightNode;
}
if (rightNode.left) {
rootNode.setRight(rightNode.left);
}
rightNode.setLeft(rootNode);
}right-left-右旋-左旋-双旋
1.先对parent节点右旋,变化为rotateRightRight情形
2.处理rotateRightRight情形rotateRightLeft
/**
* @param {BinarySearchTreeNode} rootNode
*/
rotateRightLeft(rootNode) {
const rightNode = rootNode.right;
rootNode.setRight(null);
const rightLeftNode = rightNode.left;
rightNode.setLeft(null);
if (rightLeftNode.right) {
rightNode.setLeft(rightLeftNode.right);
rightLeftNode.setRight(null);
}
rootNode.setRight(rightLeftNode);
rightLeftNode.setRight(rightNode);
this.rotateRightRight(rootNode);
}左旋
- 和retateLeftLeft情况一致
1. grandparent.left = parent.right
2. parent.parent = grandparent.parent
3. parent.right = grandparent
- 第1步和第2步可以交换rotateLeft
/**
* @param {*} rootNode
*/
rotateLeft(rootNode) {
const rightNode = rootNode.right;
rootNode.setRight(null);
if (rootNode.parent) {
rootNode.parent.setRight(rightNode);
} else if (rootNode === this.root) {
this.root = rightNode;
}
if (rightNode.left) {
rootNode.setRight(rightNode.left);
}
rightNode.setLeft(rootNode);
}右旋
- 和rotateRightRight情况一直
1. grandparent.right = parent.left
2. parent.parent = grandparent.parent
3. parent.left = grandparent
- 第1步和第2步可以交换rotateRight
/**
* @param {*} rootNode
*/
rotateRight(rootNode) {
const leftNode = rootNode.left;
rootNode.setLeft(null);
if (rootNode.parent) {
rootNode.parent.setLeft(leftNode);
} else if (rootNode === this.root) {
this.root = leftNode;
}
if (leftNode.right) {
rootNode.setLeft(leftNode.right);
}
leftNode.setRight(rootNode);
}统一处理
/**
* @param {*} r
* @param {*} a
* @param {*} b
* @param {*} c
* @param {*} d
* @param {*} e
* @param {*} f
*/
rotate(r, a, b, c, d, e, f) {
// d
d.parent = r.parent;
if (r.isLeftChild()) {
r.parent.setLeft(d);
} else if (r.isRightChild()) {
r.parent.setRight(d);
} else {
this.root = d;
}
//b-c
b.setRight(c);
// e-f
f.setLeft(e);
// b-d-f
d.setLeft(b);
d.setRight(f);
}旋转:
- 必定有旋转中心,右旋顺时针旋转,左旋逆时针旋转
- 旋转中心的节点上升,绕中心旋转的节点下沉
引用的维护:
- grandparent的父节点更新为parent节点的父节点
- 右旋必定有节点成为旋转中心的右子树
- 左旋必定有节点成为旋转中心的左子树
- 注意判空删除:
删除可能导致父节点或者祖先节点失衡,只有一个节点失衡remove
/**
* @param {*} value
*/
remove(value) {
// BinarySearchTree.remove
super.remove(value);
//
this.balance(this.root);
}
B树
一种多路搜索树
特点:
- 一个节点,可以存储超过2个元素,可以超过连个节点
- 具有二叉搜索树的性质
- 平衡m阶B树的性质
m阶:节点的度最大为m
- 1 <= 根节点的元素个数 <= m-1
- ceil(m/2) - 1 <= 非根节点的元素个数 <= m-1
- 子树(度)的个数 = 节点元素个数 + 1
- 2 <= 根节点子树的个数 <= m
- ceil(m/2) <= 非根节点子树的个数 <= m- B树和二叉搜索树在逻辑上是等价的
- 多代(层级)节点合并就可以得到一个B树节点,反之,B树节点也可以分解
- 2代二叉搜索树合并的节点,最多具有4个子树(4阶B树)
- 3代二叉搜索树合并的节点,最多具有8个子树(8阶B树)
- n代二叉搜索树合并的节点,最多具有2^n个子树(2^n阶B树)
B树的具备二叉搜索树的性质,类似二分搜索的意思
添加
- 1.B树中查找将要添加的位置,必定是叶子节点
- 2.添加可能导致当前叶子节点的元素个数 等于 B树的阶树 m 导致 上溢
- 3.解决上溢:
- 假设上溢节点为中间的某个节点k
- 将k元素和父节点合并,并且将[0,k)和(k,m-1]位置的元素分裂为2个子节点
- 向上合并肯可能导致父节点上溢,进而传播到根节点 -> 高度+1
删除
- 1.叶子节点,直接删除。元素个数低于最低限制 ceil(m/2) - 1 ,可能导致 下溢
-下溢解决:
- 此时节点元素个数必定等于ceil(m/2) - 2
- 如果相邻兄弟节点有至少ceil(m/2)个元素,可以借一个元素 => 右旋
- 兄弟节点的一个元素上升到父节点,父节点的一个元素下沉到当前节点
- 如果相邻兄弟节点只有ceil(m/2) - 1个元素,则合并
- 将父节点的元素挪下来和左右子树合并
- 合并后的元素个数 = ceil(m/2) - 1 + ceil(m/2) - 2 + 1 = 2ceil(m/2) - 2 < m - 1
- 向下合并可能导致父节点下溢,进而传播到根节点 -> 高度 - 1
- 2.非叶子节点,找到前驱或后继,替换待删除的元素,然后再删掉前驱或后继节点
- 非叶子节点的前驱或后继必定在叶子节点中
- 所以,删除的节点始终是叶子节点,同叶子节点的删除4阶B树
后续的红黑树就等价于4阶B树(2,3,4树)
红黑树
引入染色 :节点非黑即红,满足红黑树的性质则能自平衡
红黑树5大性质:
1.节点是要么是红色要么是黑色
2.根节点必是黑色
3.叶子节点都是黑色
- 按照空节点算
4.红色节点的子节点都是黑色
- 不能出现连续的红色节点(被黑色包裹)
- 存在连续的黑色节点节点
5.从任意节点到叶子节点的所有路径都包含相同数目的黑色节点等价变换:
- 红黑树和4阶B树(2,3,4树)等价
- 黑色节点和它的红色子节点融合在一起形成一个4阶B树节点
- 红黑树的黑色节点个数和等价的4阶B树节点个数相等实现红黑树
添加
4阶B树的元素个数(1 <= x <= 3),新元素的添加必定添加到叶子节点中(参考二叉搜索);
如果添加的是黑色节点,不能很好的满足红黑树的性质。如果添加的是红色节点能满足5条中的4条,因此添加新节点时默认染成红色,添加后调整。
以下列举所有的可能被添加节点(等价于4阶B树节点)的情况
(1)r<-b->r (2)b->r (3)r<-b (4)b第一种情况:
(2)b的左,(3)b的右,(4)b的左右这四种情况,直接添加,满足红黑树的性质,不做处理
第二种情况:
(2)b右边r的左右,(3)b左边r的左右这四种情况,根据uncle节点是否是红色节点,不是红色,做LL/LR,RR/RL单旋或双旋操作
LL/RR
1.parent右旋/左旋
2.parent和grandparent交换节点颜色
LR/RL
1.先对parent左旋/右旋 变换为 LL/RR情况
2.针对新的LL/RR处理
插入的新节点和parent,grandparent合并为B树的一个节点
第三种情况:
(1)b左边r的左右,(1)b右边r的左右这四种情况,根据uncle节点是否是红色节点,是红色,如果和将grandparent(黑色)合并为一个B树节点则会发生上溢
- 上溢解决
- 1.将uncle和parent染成黑色(分裂成B中的两个节点)
- 2.将grandparent染成红色当作新的待插入的节点,向上合并
- 3.插入新节点grandparent(递归),可能导致上溢向上传播直至根节点
实现:
/**
* @param {*} value
* @returns {*}
*/
insert(value) {
const insertedNode = super.insert(value);
if (this.nodeComparator.equal(insertedNode, this.root)) {
// make root always be black
this.makeNodeBlack(insertedNode);
} else {
// make all newly inserted nodes to be red
this.makeNodeRed(insertedNode);
}
// check all conditions and balance the nodes
this.balance(insertedNode);
return insertedNode;
}
/**
* @param {*} node
* @return {*}
*/
balance(node) {
if (this.nodeComparator.equal(this.root, node)) {
return;
}
if (this.isNodeBlack(node.parent)) {
return;
}
const grandParent = node.parent.parent;
if (node.uncle && this.isNodeRed(node.uncle)) {
this.makeNodeBlack(node.uncle);
this.makeNodeBlack(node.parent);
if (!this.nodeComparator.equal(this.root, grandParent)) {
this.makeNodeRed(grandParent);
} else {
return;
}
this.balance(grandParent);
} else if (!node.uncle || this.isNodeBlack(node.uncle)) {
if (grandParent) {
let newGrandParent;
if (this.nodeComparator.equal(grandParent.left, node.parent)) {
// left rotate
if (this.nodeComparator.equal(node.parent.left, node)) {
// left-left rotate
newGrandParent = this.leftLeftRotate(grandParent);
} else {
// left-right rotate
newGrandParent = this.leftRightRotate(grandParent);
}
} else {
// right rotate
if (this.nodeComparator.equal(node.parent.right, node)) {
// right-right rotate
newGrandParent = this.rightRightRotate(grandParent);
} else {
// right-left rotate
newGrandParent = this.rightLeftRotate(grandParent);
}
}
if (newGrandParent && newGrandParent.parent === null) {
this.root = newGrandParent;
this.makeNodeBlack(this.root);
}
this.balance(newGrandParent);
}
}
}删除:
todo