【论文阅读】ViT: AN IMAGE IS WORTH 16X16 WORDS 用Transformer干图像分类
AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE
用Transformer干碎CNN?
PDF Link Github Code
Section 1. Introduction
Self-Attention在NLP里很火,例如Transformer。得益于计算效率以及可伸缩性,可以在训练出一个超过100B参数的巨大的模型,而且随着模型和数据集的增长,还没有出现性能饱和的现象。
在CV领域,卷积占了绝大半壁江山。随着NLP的发展,也有许多工作尝试加入Self-Attention到CNN里面去;也有人尝试直接把卷积全替换了。
得益于Transformer在NLP里面的成功案例,计划使用一个标准的Transformer,直接把它应用到图像领域内。做法就是把图像分块,然后用一个线性编码来把分块的内容编码成一个向量,然后塞到Transformer里面去,每一个小块实际上是被当作一个word来进行处理。
在小数据集上,这个模型的效果并不算太好,在同样的模型尺寸下并不能打得过ResNet。这个糟糕的结果似乎是满足我们预期的。因为Transformer缺少一些inductive biases(归纳偏置),例如 translation equivariance以及locality。但是在塞了足够多的数据之后(14M-300M),我们发现大规模的训练摒弃了这种归纳偏置。
其实这里的归纳偏置,通俗来说就是CNN的各种设计。更常规一些的说法就是文中的描述,CNN有更好的捕捉局部信息的能力。
在ViT(Vision Transformer)中,经过大规模训练的模型能更接近甚至超越SOTA模型的性能,在ImageNet上获得了88.55%,ImageNet-ReaL上获得了90.72%,CIFAR-100上94.55%以及在VTAB上77.63%。
Section 2. Related Work
大型的基于Transformer的模型通常来说就是在一个超大的模型上预训练然后对hand部分进行任务相关的fine-tune,例如BERT,GPT之类的。笨笨地将self-attention应用到图像领域,需要图像的每一个像素都进行拉平排列,但是这么做会大量地消耗计算资源,实际运用也不现实。有一些尝试,如有把self-attention放在一些像素地局部,而非全局。此外,稀疏Transformer可用于可伸缩地近似全局self-Attention(❓)。另一个扩大注意力的替代方案是把它放在一些任意大小的块中。总的来看,这些方法在视觉领域的都产生了不错的应用结果,但是都需要一些复杂的工程设计。
与ViT最为相似的是Cordonnier et al. (2020)的工作,它们对输入图像提取2x2的块然后在头部应用完整的self-attention模块。但是ViT展示了大数据集下的预训练模型能battle一下SOTA的模型。当然,近期也有很多尝试将CNN和self-attention结合起来的工作(后面一些的文献不讲了)。
另一个类似的工作是iGPT,对降低分辨率以及减少图像空间后的图像像素使用Transformers,以一种无监督的方式对这个生成式模型进行了训练。
Section 3. Method
模型设计上,尽可能保证和原始的Transformer一模一样。这样搞的优点是开箱即用。
3.1 VISION TRANSFORMER (VIT)
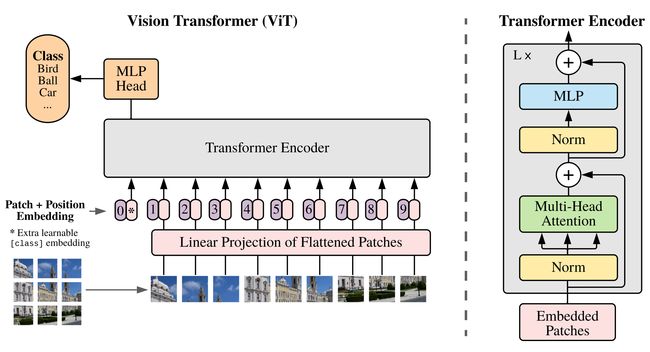
具体结构如上图所示。针对2D图像数据,把图像数据 x ∈ R H × W × C \mathbf{x} \in \mathbb{R}^{H \times W \times C} x∈RH×W×C切分成一堆2D的小块 x p ∈ R N × ( P 2 ⋅ C ) \mathbf{x}_{p} \in \mathbb{R}^{N \times\left(P^{2} \cdot C\right)} xp∈RN×(P2⋅C),其中 P P P是每个小块的大小, C C C是通道数, N = H W / P 2 N=HW/P^2 N=HW/P2。由于Transformer要求输入的数据尺寸是一些latent vector,因此对每一个图像块用一个可训练的线性映射模块来将拉平的小块映射为一个向量, 如下面第一个式子所示。最终生成的结果取个名字就叫patch embedding。
z 0 = [ x class ; x p 1 E ; x p 2 E ; ⋯ ; x p N E ] + E pos , E ∈ R ( P 2 ⋅ C ) × D , E pos ∈ R ( N + 1 ) × D z ℓ ′ = MSA ( LN ( z ℓ − 1 ) ) + z ℓ − 1 , ℓ = 1 … L z ℓ = MLP ( LN ( z ℓ ′ ) ) + z ′ , ℓ = 1 … L y = LN ( z L 0 ) \begin{aligned} \mathbf{z}_{0} &=\left[\mathbf{x}_{\text {class }} ; \mathbf{x}_{p}^{1} \mathbf{E} ; \mathbf{x}_{p}^{2} \mathbf{E} ; \cdots ; \mathbf{x}_{p}^{N} \mathbf{E}\right]+\mathbf{E}_{\text {pos }}, & \mathbf{E} \in \mathbb{R}^{\left(P^{2} \cdot C\right) \times D}, \mathbf{E}_{\text {pos }} \in \mathbb{R}^{(N+1) \times D} \\ \mathbf{z}_{\ell}^{\prime} &=\operatorname{MSA}\left(\operatorname{LN}\left(\mathbf{z}_{\ell-1}\right)\right)+\mathbf{z}_{\ell-1}, & \ell=1 \ldots L \\ \mathbf{z}_{\ell} &=\operatorname{MLP}\left(\operatorname{LN}\left(\mathbf{z}_{\ell}^{\prime}\right)\right)+\mathbf{z}^{\prime}, & \ell=1 \ldots L \\ \mathbf{y} &=\operatorname{LN}\left(\mathbf{z}_{L}^{0}\right) & \end{aligned} z0zℓ′zℓy=[xclass ;xp1E;xp2E;⋯;xpNE]+Epos ,=MSA(LN(zℓ−1))+zℓ−1,=MLP(LN(zℓ′))+z′,=LN(zL0)E∈R(P2⋅C)×D,Epos ∈R(N+1)×Dℓ=1…Lℓ=1…L
与BERT里面有的[class] token一样,除了所有的patch embedding之外,还在序列的头上设计了一个可学习的类别令牌,如上面式子第一行里的那个 x c l a s s x_{class} xclass(这里称 z 0 0 = x c l a s s z_0^0=x_{class} z00=xclass),这个token在Transformer的编码器( z L 0 z_L^0 zL0)中的状态实际上就是表示图像的表征 y y y,如上面式子的最后一行。在训练和fine-tune阶段,都会有一些额外的东西attach到这个表征上去,例如在预训练阶段是一个有一层隐藏层的MLP,在finetune阶段是一个全连接层。
以下引自用Transformer完全替代CNN
至于为什么BERT或者这篇文章的ViT要多加一个token呢?因为如果人为地指定一个embedding(例如本文中某个patch经过Linear Projection得到的embedding)经过encoder得到的结果作为整体的表示,则不可避免地会使得整体表示偏向于这个指定embedding的信息(例如图像的表示偏重于反映某个patch的信息)。而这个新增的token没有语义信息(即在句子中与任何的词无关,在图像中与任何的patch无关),所以不会造成上述问题,能够比较公允地反映全图的信息。
除了在patch embedding最前面加入一个token,由于图像本身在进行分块之后是不包含位置信息的,所以尝试加入了一个位置编码,具体的如上图所示,使用的是一个1D编码,之所以不用其他的编码方式如下表所示,因为没啥显著的效果提升。
| Pos.Emb. | Default/Stem | EveryLayer | EveryLayer-Shared |
|---|---|---|---|
| NoPos.Emb. | 0.61382 | N/A | N/A |
| 1-D Pos.Emb. | 0.64206 | 0.63964 | 0.64292 |
| 2-D Pos.Emb. | 0.64001 | 0.64046 | 0.64022 |
| Rel.Pos.Emb. | 0.64032 | N/A | N/A |
至于上式中间那两个式子,实际就是Transformer编码器的一些可替换的MSA、MLP层。此外,在每一个block的后面都加入了一个层归一化(LN),MLP有两层以及一个GELU的非线性激活。
Inductive bias
可以注意到的是视觉Transformer对比CNNs来说,有着更少的inductive bias。
前面解释了,实际上就是有更少的一些针对性地结构设计,如局部性、变化同变性(translation equivariance)之类的等等。
这里针对平移同变性再简单讲一点:
这个概念和平移不变性放在一起将比较好,平移不变性指的是对于平移前后的输入数据来说,模型的输入和输出保持不变。后者是保证数据平移前后,产生的feature map中目标的位置也同样产生了相同的平移变换。(除了位置之外,特征的值保持不变 ← \leftarrow ←这一点是由前者平移不变性保证)。
举两个例子:
1、做分类任务,一个目标的平移,最终产生的结果是一样。
2、做分割任务,一个目标的平移,分割的结果中目标也产生的相应的移动。
在整个ViT模型里面,只有MLP是具有local+translation equivariance性质的结构,剩下self-attention层都具有全局性。 在整个参数学习的过程中,2D的结构信息的使用也很少,例如在finetune阶段不同的分辨率的图像,如何保证位置信息与训练阶段时能保持一致(这个文后会细说)。这么来看,所有patches之间的空间关系信息都得从0学起。
Hybrid Architecture
除了将原始图像进行分块,很自然而然的一点当然是也可以将特征图进行分块,这样就可以与CNN进行结合。当然这与前面Section2 Related Works里描述的一些工作会有些不一样。
3.2 FINE-TUNING AND HIGER RESOLUTION
简单的看,利用预训练模型进行finetune只要把prediction head换成一个0初始化的 D × K D\times K D×K的前馈层就可以了,其中 K K K表示子任务的类别数。但当喂高分辨率数据的时候,要保证patch的大小不变就有点困难,维持patch不变就会导致patch的个数增加。虽然Transformer可以处理任意长度的编码,但是一旦长度变了之后,(预训练模型的)位置编码的意义就等价于消失了。对应的解决方案是对预训练模型里面的位置编码进行插值,保证位置编码的个数的一致,也就是手动把整个2D的位置信息进行了拉长和缩短。
Section 4. Experiments
测试了ResNet,ViT以及Hybrid模型。
这里一些设置什么的不做描述,有兴趣自己读一下论文,后面仅展示一些直观的图表。
下表展示了一些SOTA模型在各个数据集上的性能,单位都是准确率。
| Ours-JFT | Ours-JFT | Ours-I21K | BiT-L | NoisyStudent | |
|---|---|---|---|---|---|
| ViT-H/14 | ViT-L/16 | ViT-L/16 | ResNet152x4 | EfficientNet-L2 | |
| ImageNet | 88.55 ± 0.04 | 87.76 ± 0.03 | 85.30 ± 0.02 | 87.54 ± 0.02 | 88.4/88.5* |
| ImageNetReaL | 90.72 ± 0.05 | 90.54 ± 0.03 | 88.62 ± 0.05 | 90.54 | 90.55 |
| CIFAR-10 | 99.50 ± 0.06 | 99.42 ± 0.03 | 99.15 ± 0.03 | 99.37 ± 0.06 | − |
| CIFAR-100 | 94.55 ± 0.04 | 93.90 ± 0.05 | 93.25 ± 0.05 | 93.51 ± 0.08 | − |
| Oxford-IIITPets | 97.56 ± 0.03 | 97.32 ± 0.11 | 94.67 ± 0.15 | 96.62 ± 0.23 | − |
| OxfordFlowers-102 | 99.68 ± 0.02 | 99.74 ± 0.00 | 99.61 ± 0.02 | 99.63 ± 0.03 | − |
| VTAB(19tasks) | 77.63 ± 0.23 | 76.28 ± 0.46 | 72.72 ± 0.21 | 76.29 ± 1.70 | − |
| TPUv3-core-days | 2.5k | 0.68k | 0.23k | 9.9k | 12.3k |
下图左图展示了虽然ViT模型在ImageNet(低数据量)情况下效果不如BiT ResNet但是在大数据量上,ViT的性能指标一下就上来了。右图展示了finetune过程的一些试验结果,横坐标是预训练图像的数量。其中ViT-b是ViT-B同样的结构但是减半了所有隐藏层的数量。
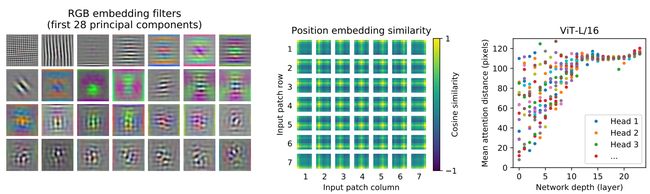
前面的公式的一行是对输入数据进行编码,具体咋编码的呢,对ViT-L/32的线性层提取一个主成分然后可视化如下图左边所示。具体的看就是这些组件将patch内的信息进行的低维编码。中间的图中的小tiles是图像的小块之间位置编码的余弦相似度。这里解释了为什么使用2D信息的位置编码并不能显著提升最终的性能,因为最终一定会学成2D样式的位置编码信息,这里可以看一下文章附录D。右图展示了attention的激活激活区域随着网络层数的加深产生的变化。
Section 5. CONCLUSION
这里可以看一下文章附录D。右图展示了attention的激活激活区域随着网络层数的加深产生的变化。
[外链图片转存中…(img-BfbQ487L-1611395825256)]
Section 5. CONCLUSION
没啥好说的,就是总结而已