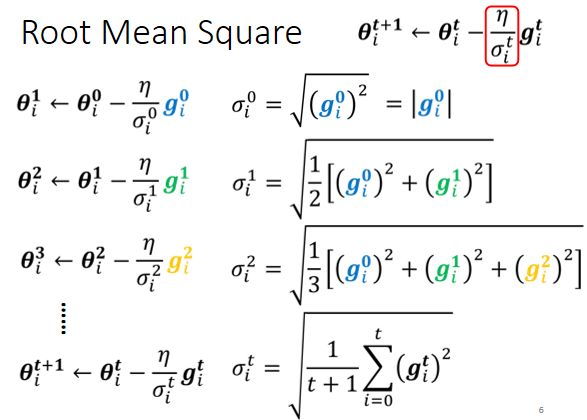李宏毅深度学习2021春p5-9：神经网络训练技巧

李宏毅深度学习2021春p5-9：神经网络训练技巧

兄弟萌也可以到我的博客康康：冬于的博客

训练遇到的问题

1. 参数不断的更新,training loss一开始下降，然后不会再下降，但距离0还有很远的gap；
2. 一开始model就train不起来，不管怎么update参数，loss一直比较大。

导致上述问题的原因可能有很多，我们先回忆一下梯度下降算法在现实世界中面临的挑战：

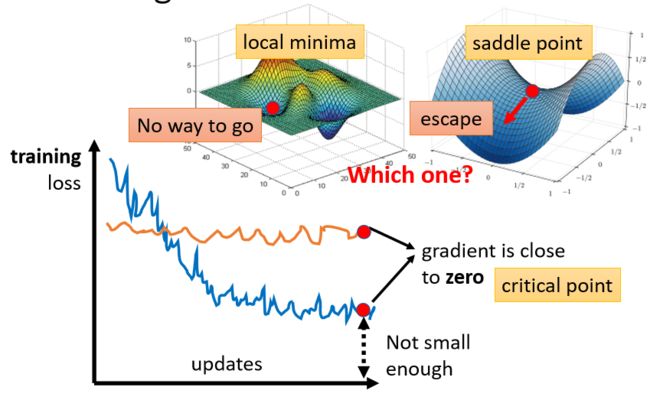
• 问题1：局部最优（Stuck at local minima）
• 问题2：等于0（Stuck at saddle point）
• 问题3：趋近于0（Very slow at the plateau）

像这种gradient为0的点，统称critical point，我们先从问题1和问题2来看看如何“炼丹”。

局部最小值local minima和鞍点saddle point

Critical Point

gradient为0的点。

local minima

**现在所在的位置已经是局部loss最低的点，**往四周走 loss都会比较高，可能没有路可以走。

saddle point

**saddle point从某个方向还是有可能到达loss更低的位置，**只要逃离saddle point，就有可能让loss更低。

如何判断某个位置是local minima还是saddle point？

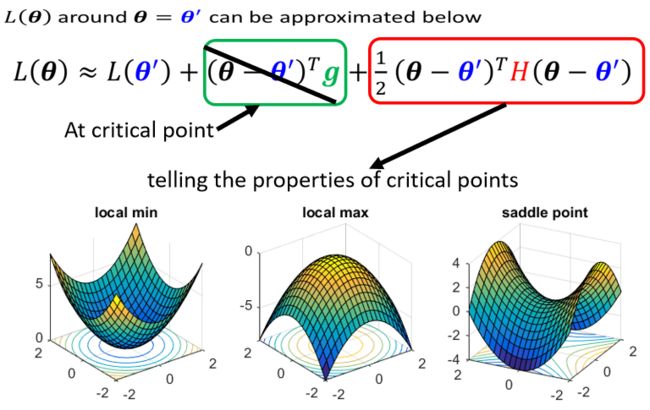
通过泰勒级数展开估计（Tayler Series Approximation）loss function的形状。

也就是，虽然无法完整、准确写出$L(\theta )$，但如果给定某一组参数${\theta }^{\prime }$，在${\theta }^{\prime }$附近的loss function可以通过泰勒级数展开来估计：

• 第一项$L({\theta }^{\prime })$：当$\theta$跟${\theta }^{\prime }$很近的时候,$L(\theta )$跟$L({\theta }^{\prime })$比较靠近，但还有一些差距；
• 第二项$(\theta -{\theta }^{\prime }{)}^{T}g$：是一个向量,这个$g$是gradient，这个gradient会来弥补${\theta }^{\prime }$跟$\theta$之间的差距。有时候gradient会写成$\nabla L({\theta }^{\prime })$，它的第$i$个component,就是$\theta$的第$i$个component对$L$的微分，加上这一项之后仍然还有差距；
• 第三项中$(\theta -{\theta }^{\prime }{)}^{T}H(\theta -{\theta }^{\prime })$：其中$H$跟Hessian有关，是一个矩阵，第三项会再补足与真正的L(θ)之间的差距。$H$是L的二次微分构成的矩阵,它第$i$个row,第$j$个column的值$H_{ij}$，是把$\theta$的第$i$个component,对$L$作微分,再把$\theta$的第$j$个component,对$L$作微分,也就是做两次微分以后的结果 。

总的来说，$L(\theta )$跟两个东西有关,跟gradient有关，跟hessian有关。gradient就是一次微分,hessian是内含二次微分的项目。

如果我们今天走到了一个critical point，意味着上式中$g=0$，只剩下$L({\theta }^{\prime })$和红色的这一项：

于是可以通过红色这一项判断${\theta }^{\prime }$附近的error surface长什么样，从而判断现在是在local minima、local max还是saddle point。

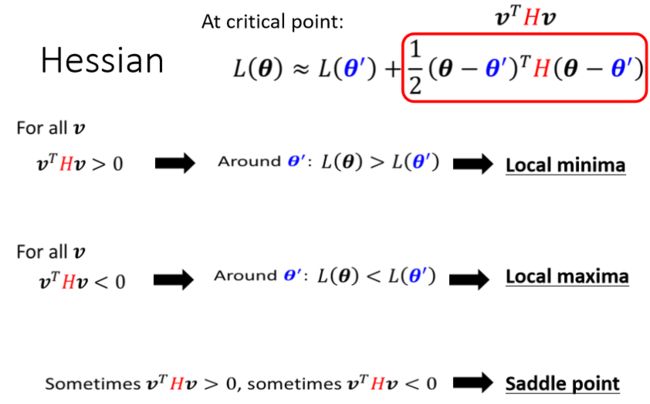
通过Hession矩阵判断${\theta }^{\prime }$附近的error surface

把$(\theta -{\theta }^{\prime })$用向量$v$来表示，根据$v^{T}Hv$的值来判断：

线性代数中，如果所有的$v$带入$v^{T}Hv$的值都大於零，那$H$叫做positive definite 正定矩阵。所以我们不需要通过穷举所有的点来判断$v^{T}Hv$是大于零还是小于零，而是直接利用$H$是否正定来判断。而判断$H$是否是正定矩阵可以通过求解$H$的特征值来判断。如果所有的eigen value特征值都是正的，那么$H$就是positive definite 正定矩阵。

所以判断条件就转化为：

如何逃离saddle point？

**$H$不只可以帮助我们判断,现在是不是在一个saddle point,还指出了参数可以update的方向。**注意这个时候$g=0$。

根据$\lambda x=Ax$，可以对式子进行转化：

于是如果$\lambda <0$（eigen value<0）,那$\lambda \Vert u\Vert ²<0$，所以eigen value是负的,那这一整项就会是负的,也就是$u^{T}Hu$是负的，也就是红色整项是负的，于是$L(\theta )<L({\theta }^{\prime })$。也就是说令$\theta -{\theta }^{\prime }=\mu$，在${\theta }^{\prime }$的位置加上$\mu$,沿$\mu$的方向做update得到$\theta$,就可以让loss变小。

这个方法也有一点问题：$H$的运算量非常非常的大，还需要算其特征值和特征向量，运算量惊人，实际操作中还有其他方法可以逃离saddle point，在最糟糕的情况下还有这种方法可以逃离。

Saddle Point v.s. Local Minima

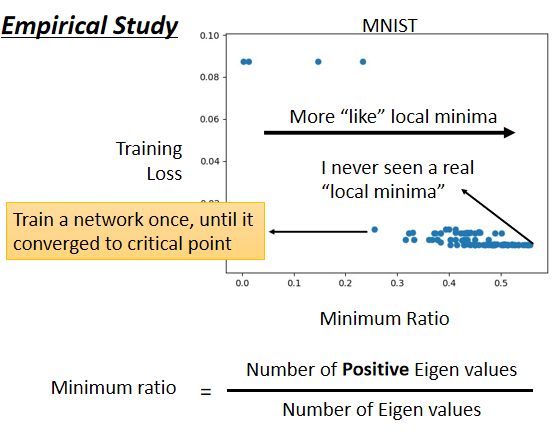
**事实上Local Minima没有那么常见。**一个可能的解释是：在低维的空间中,低维的一个参数的error surface,好像到处都是local minima,但是在高维空间来看,它可能只是一个saddle point。

如下图所示，几乎找不到完全所有eigen value都是正的critical point。下图这个例子种，minimum ratio代表正的eigen value的数目占总数的比例，最大也在0.5~0.6,代表只有一半的eigen value是正的,还有一半的eigen value是负的。

在这个图上,越往右代表critical point越像local minima,但是它们都没有真的,变成local minima。

batch/mini-batch和动量Momentum

batch/mini-batch

Optimization with Batch

每次在 Update 参数的时候，拿一个batch出来,算个 Loss,算个 Gradient,Update 参数,然后再拿另外个batch,再算个 Loss,算gradient，更新参数，以此类推。

mini-batch就是不把所有训练数据拿出来一起算loss，而是分小块。

所有的 Batch 训练过一遍,叫做一个 Epoch。

在生成batch的时候长春会做shuffle。

Shuffle 有很多不同的做法，常见的一个做法是在每一个 Epoch 开始之前,会分一次 Batch，每一个 Epoch 的 Batch 都不一样。

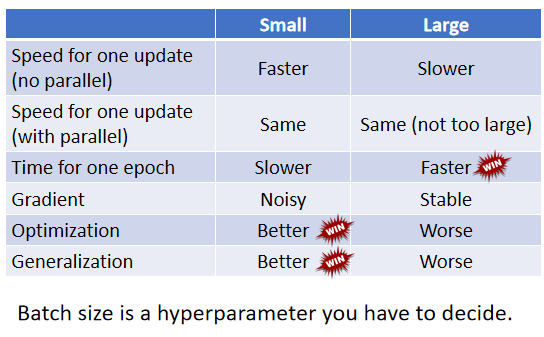
为什么要batch

直接上对比图：

之前提到，更大的batch在看完更多的example后才会更新一次参数，但更新方向可能比小batch更准确（powerful，而小batch可能更noisy）如果都是串行的话，看上去更大的batch的参数更新速度更慢。

但实际上，在有并行计算条件下，比较大的 Batch Size算 Loss再进而算 Gradient所需要的时间,不一定比小的 Batch Size 要花的时间长。而更小的batch一个epoch的时间更长。（一个用于MINIST数据集上的实验如下图。）

所以看上去big batch的时间劣势消失了，那是不是big batch更好呢？

答案是否定的，神奇的地方是 Noisy 的 Gradient,反而可以帮助 Training。

同一个model，batchsize过大效果反而更差？

用过大的batch size optimizer可能会有问题。

拿不同的 Batch 来训练模型，可能会得到下图的结果：

Batch Size 越大,Validation Acc 上的结果越差。但这个不是 Overfitting，因为如果 Training也是 Batch Size 越大，Training 的结果越差。

现在用的是同一个模型，它们可以表示的 Function 就是一模一样的，所以这个不是 Model Bias 的问题。这个是 Optimization 的问题,代表当用大的 Batch Size 的时候, Optimization 可能会有问题，小的 Batch Size,Optimization 的结果反而是比较好的。

为什么小的 Batch Size在 Training Set 上会得到比较好的结果？

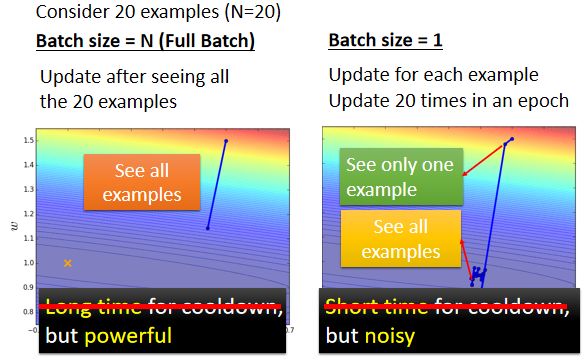
一个可能的解释是这样子的，如下图所示：

• 假设是 Full Batch，沿著一个 Loss Function 来 Update 参数，走到一个 Local Minima/saddle Point，显然就停下来了，Gradient 是零，可能就没办法更新参数了；
• 假如是 Small Batch 的话，因为**每次挑一个 Batch 出来算它的 Loss，所以每一次 Update 你的参数的时候，用的 Loss Function 都是略有差异的。**选到第一个 Batch 的时候,，是用 L1 来算 Gradient；选到第二个 Batch 的时候，用 L2 来算Gradient。**假设用 L1 算 Gradient 的时候,发现 Gradient 是零，卡住了，但 L2 它的 Function 和 L1 又不一样，L2 就不一定会卡住。**所以在某一个batch卡住了没关系，还是有办法 Training Model，还是有办法让 Loss 变小。所以mini-batch这种 Noisy 的 Update 的方式，结果反而对 Training是有帮助的。

另外一个神奇的事：小的batch在testing也有帮助

论文On Large-Batch Training For Deep Learning,Generalization Gap And Sharp Minima中，就做了这样一个实验：努力的调big- Batch 的 Learning Rate,然后想办法把big-Batch的训练模型,跟small-Batch 训练得得一样好，结果发现small-Batch在 Testing 的时候是比较好的。

注意这个时候big-batch在训练集中表现和small-batch性能相似，但在测试集表现更差说明的问题才是over fitting。

为什么会这样呢？文章也给了一个解释：

假设这个实线是 Training Loss，那在这个 Training Loss 上面，可能有很多个 Local Minima，这些 Local Minima 它们的 Loss 都很低，它们 Loss 可能都趋近于 0。但是 Local Minima还是有好 Minima 跟坏 Minima 之分。

• 好的Local Minima：在一个平原上（左边的）；
• 坏的Local Minima：在一个峡谷里面（右边的）。

为什么这么判定呢？

假设现在 Training 跟 Testing 中间,有一个 Mismatch，Training 的 Loss 跟 Testing 的 Loss,它们的Function 不一样。导致这种mismatch的原因可能有两个：

1. 可能是本来 Training 跟 Testing 的 Distribution就不一样；
2. 那也有可能是因为 Training 跟 Testing都是从 Sample 的 Data 算出来的，也许 Training 跟 Testing Sample（采样）到的 Data 不一样，那它们算出来的 Loss,自然有一点差距。

那我们就假设这个 Training 跟 Testing的差距就是把 Training 的 Loss,这个 Function 往右平移一点（上图虚线为testing loss）。这时候会发现，对左边这个在一个盆地的 Minima 来说，它的在 Training 跟 Testing 上面的结果,不会差太多；但是对右边这个在峡谷的 Minima 来说，就差别很大。

它在这个 Training Set 上算出来的 Loss 很低，但是因为 Training 跟 Testing 之间的mismatch，所以 Testing 的时候，这个 Error Surface 变化后，算出来的 Loss 就变得很大。所以猜想这个大的 Batch Size，会让模型倾向于走到峡谷里面,而小的 Batch Size,倾向于让模型走到盆地裡面：

• 因为小的 Batch有很多的 Loss，每次 Update 的方向都不太一样，所以如果这个峡谷非常地窄，可能一个不小心就跳出去了，因为每次 Update 的方向都不太一样，它的 Update 的方向也就随机性，所以一个很小的峡谷，没有办法困住小的 Batch。如果峡谷很小，它可能动一下就跳出去，之后如果有一个非常宽的盆地，它才会停下来；
• 而对于大的 Batch Size，就是顺着规定 Update，它就很有可能，走到一个比较小的峡谷里面。

但这只是一个解释，实际上这个还是一个尚待研究的问题。

总结batch/mini-batch

总的来说，大的 Batch 跟小的 Batch,它们各自有它们擅长的地方，**Batch Size,变成另外一个需要去调整的 Hyperparameter。**一些论文也讨论了如何兼顾鱼和熊掌，需要用一些特殊的方法来解决大的Batch Size 可能会带来的劣势：

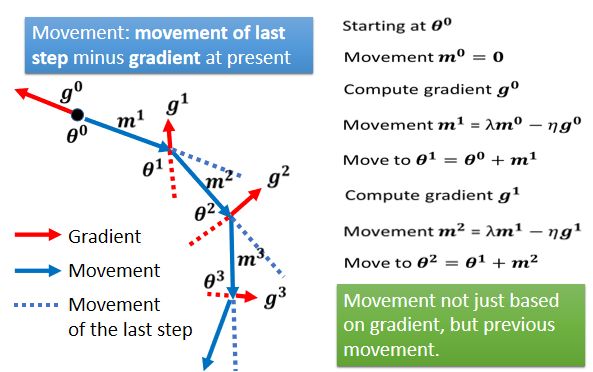
Momentum

Momentum是另外一个有可能可以对抗 Saddle Point,或 Local Minima 的技术。

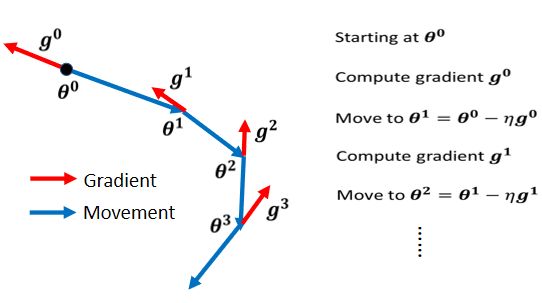
传统的梯度下降

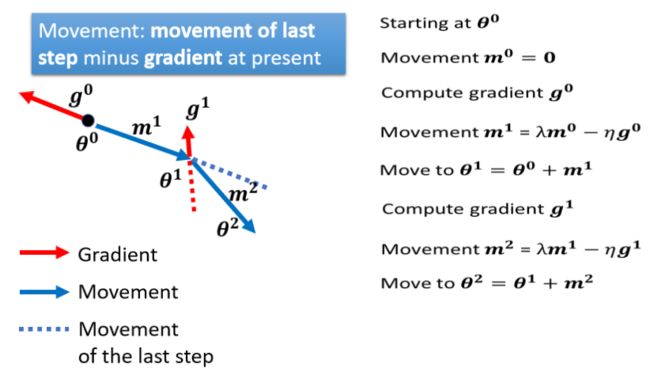
Gradient Descent + Momentum

加上 Momentum 以后,每一次在移动参数的时候,不是只往 Gradient 的反方向来移动参数,是 Gradient 的反方向+前一步移动的方向去调整去到参数

具体来看步骤如下：把蓝色的虚线加红色的虚线,前一步指示的方向跟 Gradient 指示的方向,当做参数下一步要移动的方向。

下面有一个例子来展示：

在第三步，Gradient 变得很小，但是没关系，如果有 Momentum 的话，根据上一步的Momentum 可以继续往前走；

甚至走到第四步时，Gradient 表示应该要往左走了，但是如果前一步的影响力,比 Gradient 要大的话，还是有可能继续往右走,甚至翻过一个小丘,可能可以走到更好 Local Minima。

自动调整学习率Adaptive Learning Rate

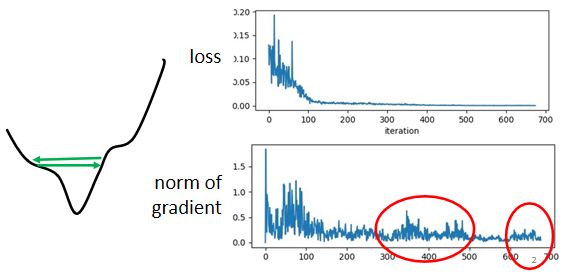
critical point不一定是训练过程中最大的阻碍，思考一个问题：

loss不再下降的时候，gradient真的很小吗？

并不是的。如下图所示虽然loss不再下降,但是这个gradient的大小并没有真的变得很小。它可能在error surface山谷的两个谷壁间,不断的来回的震荡。

所以有的时候训练不下去的原因不是critical point,而是其他的原因。

举个例子：

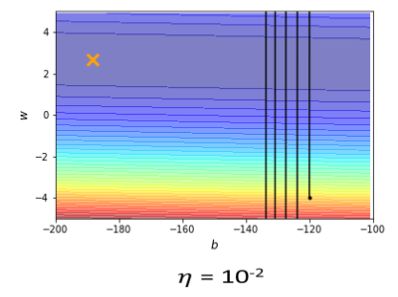
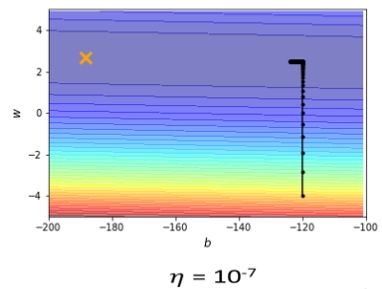
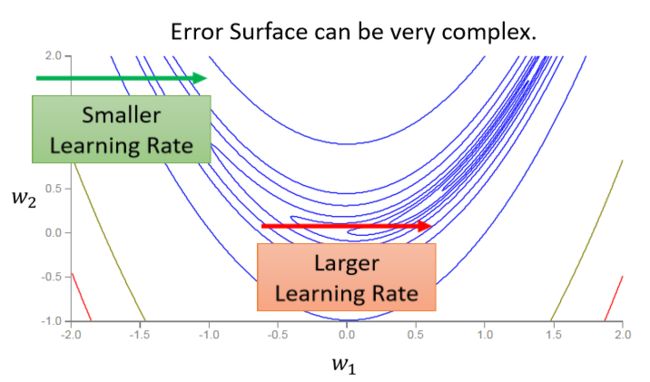
在下面这个error surface中，纵轴的参数变化很小就会导致结果变化很大，而横轴参数变化很大结果变化很小。

如果两个参数使用同一个学习率，当学习率调的过大，在纵轴方向可能直接震荡：

如果学习率调的很小，在纵轴可以逐渐找到好的参数，但是在横轴更新时，由于学习率过小，更新速度太慢，也很难找到最优解。

所以可以考虑为不同的参数和不同的iteration设置不同的learning rate。

上面的案例展示了学习率选择的两个大原则：

1. 如果在某一个方向上,gradient的值很小,非常的平坦,那learning rate调大一点；
2. 如果在某一个方向上非常的陡峭,坡度很大,那其实learning rate可以设得小一点；

learning rate自动调整策略：为不同的参数和不同的iteration设置不同的learning rate

以一个参数${\theta }_i$为例：

原始策略：
$${\theta }_i^{t+1}\leftarrow {\theta }_i^t-\eta g_i^t$$
不同的参数和不同的iteration自动调整策略：
$${\theta }_i^{t+1}\leftarrow {\theta }_i^t-\frac{\eta }{{\sigma }_t^t}{g}_i^t$$
上式中${\sigma }_i^t$的下标$i$代表它是depend on $i$的，也就是不同参数有不同的$\sigma$，而上标$t$表示它是iteration dependent的,不同的iteration会有不同的σ。因此$\frac{\eta }{{\sigma }_t^t}$变成parameter dependent的learning rate。

那么如何计算$\sigma$呢？

常见的计算$\sigma$可以用gradient的Root Mean Square，这种计算方法也被用于Adagrad这一优化器中。

用于Adagrad中的Root mean square

Root mean square计算$\sigma$是通过求历史梯度的均方根得到的，计算步骤如下图所示：

为什么Root mean square可以做到坡度比较大的时候,learning rate就减小,坡度比较小的时候,learning rate就放大呢?

看看下面这个例子：

现在我们有两个参数:$\theta ᵢ¹$和$\theta ᵢ²$ ，$\theta ᵢ¹$坡度小 $\theta ᵢ²$坡度大。

$\theta ᵢ¹$因为坡度小,所以在$\theta ᵢ¹$这个参数上面,算出来的gradient值都比较小，那么$\sigma$也比较小，$\frac{\eta }{\sigma }$就比较大。

所以有了$\sigma$这一项以后,就可以随iteration gradient的不同,每一个参数的gradient的不同,来自动的调整learning rate的大小。

但是，就算是同一个参数,它需要的learning rate,也可能会随时间而改变，于是还有进阶版的策略自适应learning rate。

RMSProp

同一个参数同一个方向也希望可以自适应调整，比如下面这个新月形的error surface。

在水平方向（同一参数同一方向）在绿色箭头这个地方坡度比较陡峭，需要比较小的learning rate，走到了中间这一段，到了红色箭头坡度又变得平滑，需要比较大的learning rate。

RMSProp和Apagrad在计算$\sigma$时，第一步时一样的，在第二步更新时，通过一个超参数$\alpha$赋予了历史梯度和当前梯度不一样的权重（而Apagrad中是一样的权重，也就是每一个gradient同样重要）。

计算过程如下图所示：

α就像learning rate一样是一个hyperparameter，需要自己调整：

• 如果α设很小趋近于0,就代表我觉得**$gᵢ¹$相较于之前所算出来的gradient而言,比较重要**；
• α设很大趋近于1,那就代表现在算出来的$gᵢ¹$比较不重要,之前算出来的gradient比较重要。

举个例子看一下RMSProp的效果：

下图中，一开始梯度很小，学习率较大；

到第三步时，梯度变大，原来的Adagrad反应比较慢，可能还会用比较大的学习率，但如果用RMS Prop，把α设小一点，也就是让新的gradient影响比较大，可以很快的让σ的值变大，于是很快的让学习率变小。

还记得前面提到了momentum这个方法，RMSProp+momentum就得到了一个高级版的策略：Adam。

Adam论文链接

tips

这些优化器在pytorch等框架中都写好了，其中也包括很多超参数。李宏毅老师还提到往往用默认的超参数就够好了，自己调有时候反而会调到比较差的，炼丹玄学~

learning rate scheduling

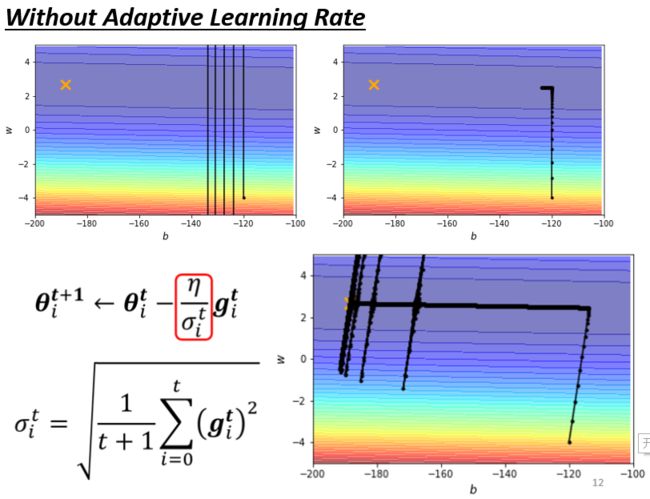
现在让我们回到前面提到的error surface上，加上Adagrad方法后，训练效果如下图右下角的子图所示：

加了Adagrad以后，在横轴方向learning rate会自动变大，从而能尽快接近最优解。但我们可以看到一个奇怪的现象，走到非常接近终点的位置，梯度突然爆炸了，这是为什么呢？

从Adagrad的$\sigma$计算方式可以回答这个问题，计算$\sigma$时，把过去所有看到的gradient,都拿来作平均：

• 所以这个纵轴的方向，在初始的时候gradient很大，学习率比较小；

• 可是继续走了很长一段路以后，gradient算出来都很小，于是y轴的方向就开始积累很小的σ；

• 累积到一个地步以后，学习率就变很大，于是发生爆炸；

• 爆炸后其实也没关系，因为爆炸后就走到gradient比较大的地方，于是σ又慢慢的变大，参数update学习率又慢慢的变小。

• 但是累计一段时间又会爆炸，然后恢复，反复。

解决这种问题的策略是learning rate scheduling，这里介绍两种：

1. Learning Rate Decay（学习率衰减策略）
2. warm up

Learning Rate Decay（学习率衰减策略）

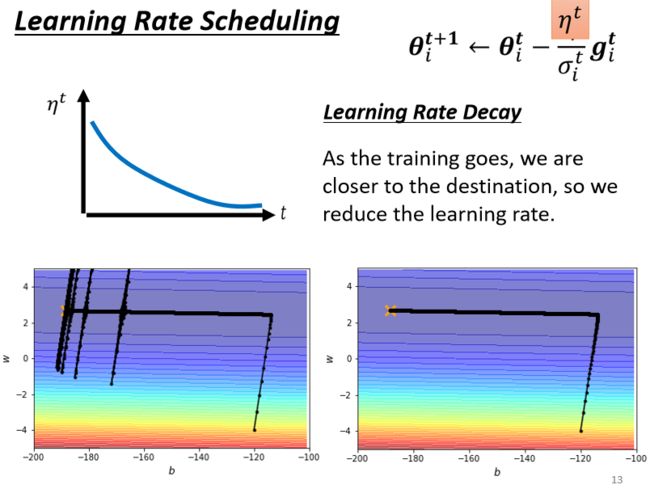
在前面使用的Adagrad中，$\eta$被当作一个固定的值，而learning rate scheduling是指让$\eta$和时间有关，常见的策略为：Learning Rate Decay（学习率衰减策略），随着训练不断进行，参数不断更新，$\eta$越来越小。

于是：一开始距离终点很远，随着参数不断update，距离终点越来越近，把learning rate减小，让参数更新减速，所以前面的那个问题，加上Learning Rate Decay可以解决。

warm up

Warm Up的方法是让learning rate,要先变大后变小。**其中变大到多大、变大速度、变小到多小、变小速度都是超参数。**如下图所示：

但是为什么需要Warm Up，为什么Warm Up有效都是待研究的问题，但在很多文献中，它就是work了，比如BERT、transformer等等模型中都用到了warm up这个技术。

李宏毅老师提到了一个可能的解释：

​ 当我们在用Adam RMS Prop，或Adagrad的时候，需要计算σ，它是一个统计的结果，σ告诉我们，某一个方向它到底有多陡,或者是多平滑，这个统计的结果，要看得够多笔数据以后才比较精确，所以一开始我们的统计是不精确的。于是我们一开始不要让参数走离初始的地方太远，先让它在初始的做一些探索。所以一开始learning rate比较小,是让它探索 收集一些有关error surface的情报，先收集有关σ的统计数据，等σ统计得比较精準以后，在让learning rate呢慢慢地增大。

自动调整学习率方法总结

我们逐步将原始梯度下降方法进行优化：

1. 加入momentum；
2. 加入自适应iteration和参数的$\sigma$；
3. 使用自适应iteration的$\eta$；

注意：momentum和$\sigma$虽然都与过去所有的gradient有关，一个放在分母，一个放在分子，但是momentum考虑了方向，而$\sigma$只考虑了gradient的大小。

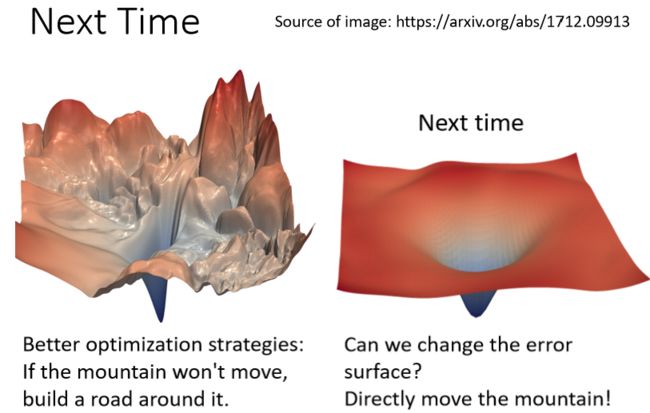
另一个角度-铲平error surface？

之前考虑的常见都是假设error surface非常崎岖情况下怎么找到比较好的参数，但其实我们可以从error surface出发，考虑如何把error surface变成一个比较平坦的，好训练的error surface，如下图所示：

通过修改损失函数和batch normalization可能可以做到修改error surface，让模型更好训练。

损失函数loss function

在讲分类模型的时候，李宏毅老师解释了为什么cross entropy更常用在分类上 ，并且用一个例子展示了loss function对error surface的影响。

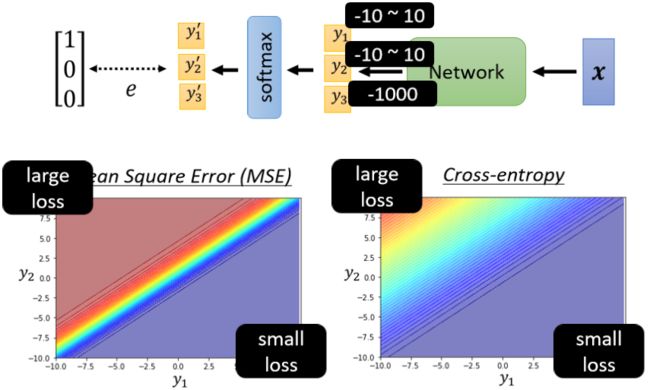
我们这里直接看这个例子：

现在我们用下面这个模型做一个3个Class的分类任务，下面两个坐标系中的图是当loss function分别设定为Mean Square Error和Cross-entropy的时候，算出来的Error surface（$y₁、y₂$的变化对loss的影响）。在红色部分（左上角）loss很大，蓝紫色部分（右下角）loss比较小。所以我们希望在训练后，参数走到右下角的地方。

假设我们开始的地方,都是左上角：

• 如果loss function 是Cross-Entropy，那么error surface的左上角这个地方是有斜率的，所以可以通过gradient descent一路往右下的地方走；
• 如果loss function 是Mean square error的话，Mean square error在左上角这种Loss很大的地方，是非常平坦的，也就是说它的gradient是非常小趋近于0的。如果初始的时候在这个地方，离目标非常远，它gradient又很小，就会没有办法用gradient descent顺利的走到右下角的地方去（当然用Adam还是有可能可以成功训练起来的，不过训练起步比较慢，训练更困难）。

总结loss function

由此例可以发现，Loss function的定义也可能影响error surface从而影响Training，选一个合适的loss function可以改变optimization的难度。

这里补充一个资料，对于一些常见任务应该选择什么样的loss function进行了总结。深度学习中常见的激活函数与损失函数的选择与介绍

batch normalization

Batch Normalization是修改error surface，让模型更好训练的其中一个方法。

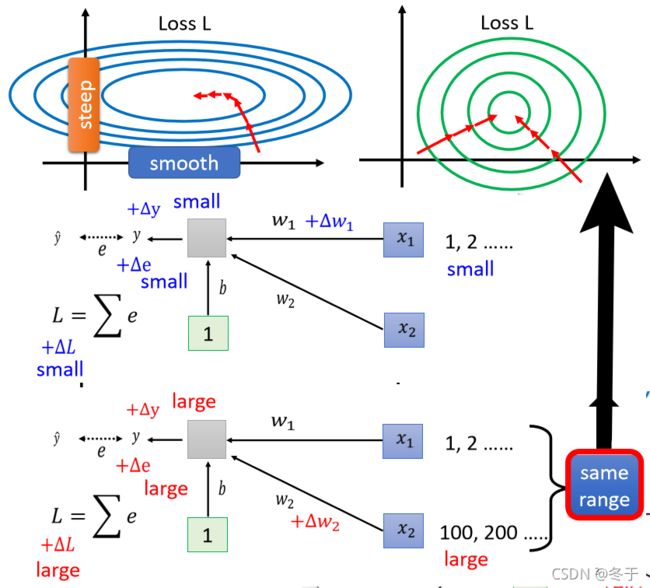
比如现在有两个参数，它们对 Loss 的斜率差别非常大，在$w_1$这个方向上面斜率变化很小，在$w_2$这个方向上斜率变化很大。如下图左边所示。

之前提到用daptive 的 learning rate，比如Adam 等等比较进阶的 optimization 的方法去更新参数，其实另一个角度就是**把这种很难训练的error surface改掉，**改成下图中右边所示。

于是我们需要思考：斜率差很多的这种状况，到底是哪里来的？

假设我们的模型上图中下半部分的简单模型：

• 输入的$x_1$很小，$w_1$有小小的改变，对输出$y$的影响比较小，对$L$的影响也小；
• 如果$x_2$取值很大，$w_2$变化很小也会造成$y$很大的变化，于是对$L$的影响也大；
• 所以如果$x_1,x_2$的取值范围差别过大（每一个 dimension 的值scale 差距很大）会导致不同方向斜率差别很大。

因此，**希望给不同的 dimension，同样的数值范围（转为上图右边部分），将原本的error surface变成比较好训练的error surface。**可以完成这个操作的方法统称为feature normalization。

feature normalization

feature normalization可以让Loss 收敛更快一点，让梯度下降更顺利一点。

下面举一个常用的feature normalization方法：利用均值和方差进行标准化standardization。

假设$x^1$到$x^R$是所有的训练数据的 feature vector，把所有训练数据的 feature vector ,统统都集合起来，$x_1^1$代表$x_1$的第一个 element,$x_1^2$就代表$x_2$的第一个 element,以此类推。

把不同样本即不同 feature vector,同一个 dimension 里面的数值计算均值mean $m_i$，并且计算第 $i$ 个 dimension 的标准差standard deviation ${\sigma }_i$。

然后用下式进行标准化standardization，然后用标准化后的${\tilde{x}}_i^r$作为模型的输入。
$${\tilde{x}}_i^r\leftarrow \frac{x_i^r-m_i}{{\sigma }_i}$$
示意图如下：

做完 normalize 以后，这个 dimension 上面的数值平均是 0， variance是 1，所以一排数值的分布就都会在 0 上下。对每一个 dimension都做一样的 normalization,就会发现所有 feature 不同 dimension 的数值都在 0 上下，那可能就可以构造比较好的 error surface。

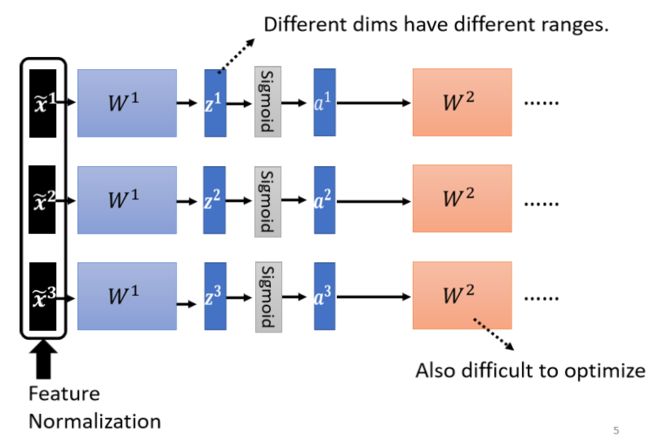
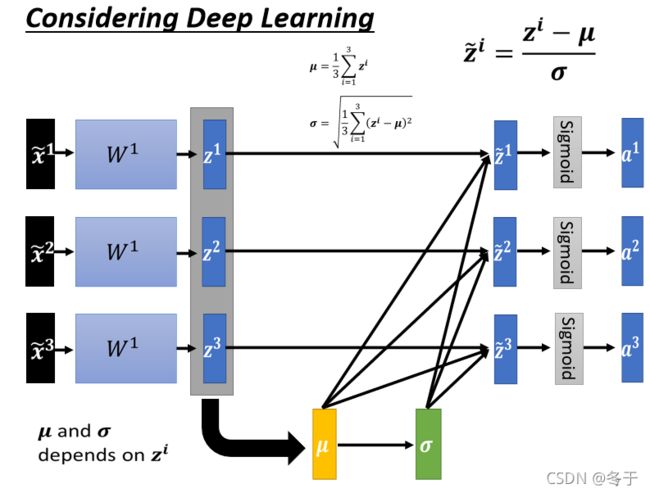
feature normalization for deep learning

我们先用feature normalization对最原始的输入做了处理得到$\tilde{x}$，那么经过第一层参数时，我们的输入各个维度的scale就是差不多的，但是深度学习的模型都是有很多层的，像下图这样**：上一层的输出是下一层的输入，那么经过了一层神经网络的特征（输出$z^1$或经过sigmoid层的输出$a^1$）各个维度可能又会有不同的scale。**

所以我们可以对$z$或者$a$做normalization。这里也有一个tips：

• 一般来说，这个 normalization,要放在 activation function 之前,或之后都是可以的，在实操上，可能没有太大的差别。
• 不过，如果选择的是 Sigmoid作为激活函数，那可能比较推荐对 $z$ 做 Feature Normalization因为Sigmoid 是一个 s 的形状，它在 0 附近斜率比较大。所以如果对$ z$ 做 Feature Normalization，把所有的值都挪到 0 附近，算 gradient 的时候值会比较大。
• 因为激活函数不一定是选 sigmoid，所以也不一定要对$z$做 Feature Normalization，如果是选别的激活函数，也许对$a$做normalization可能会有好的结果。

我们这边假设对$z$做feature normalization，举个例子：

和之前对$x$做的操作类似，对$z$也是计算均值和方差，然后进行归一化：

这里有个地方需要特别注意：

上图中的$\mu$跟$\sigma$ ,它们其实都是根据$z^1,z^2,z^3$算出来的，那么：

• 如果没有做feature normalization，因为$\tilde{x}$是处理后单独输入的，修改$z^1$只会影响${\tilde{z}}^1$和$a^1$；
• 做了feature normalization后，修改$z^1$会影响$\mu$和$\sigma$，进而不仅影响${\tilde{z}}^1$和$a^1$，还会影响${\tilde{z}}^2$和$a^2$、${\tilde{z}}^3$和$a^3$；
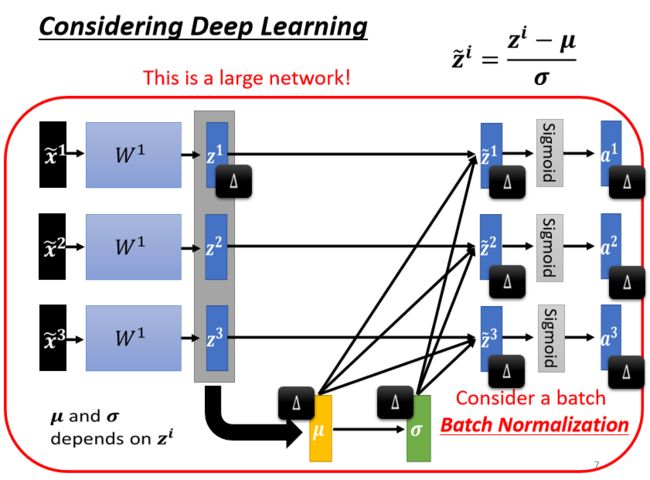
• 于是这三个 example,它们变得彼此关联了。如下图所示：

因为彼此关联，于是整个process（包括根据feature算均值方差）就变成了network的一部分，所以现在变成一个比较大的network，如下图所示。

• 之前的 network,都只输入一个 input,得到一个 output；
• 现在有一个比较大的 network是输入一堆 input,用这堆 input 在这个 network 里面，要算出均值和方差,然后输出一堆 output。

自然而然地产生一个问题，是不能一次性把很大的一个训练集全部输入网络中训练的，因为内存有限。

再自然而然地就可以考虑不输入全部的数据，而是输入一部分（batch），每次只考虑一个batch里的样本，所以在实际操作中，是对一个batch做normalization，于是这个方法叫batch normalization。

normalization in each batch - batch normalization

显然一定要有一个够大的 batch，才算得出均值和方差，假设batch size=1，那么均值和方差就没啥好算的。

所以Batch Normalization适用于 batch size 比较大的时候。相当于我们用一个batch size的训练数据分布估计整个数据集的数据分布。如果 batch size 比较大，也许这个 batch size 里的 data足以表示整个 corpus 的分布。这个时候就可以把对整个 corpus做 Feature Normalization改成只在一个 batch做 Feature Normalization。

进阶的batch normalization

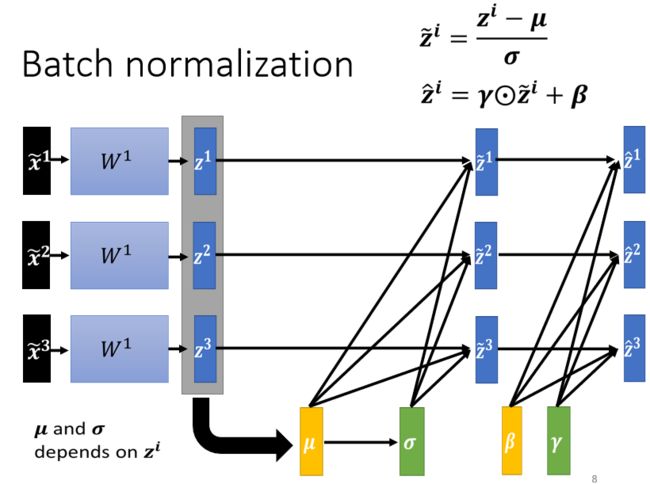
在做 Batch Normalization 的时候，往往还会对计算出来的$\tilde{z}$进行下一步操作，得到最终的$\hat{z}$：
$${\hat{z}}^i=\gamma \odot {\tilde{z}}^i+\beta$$
其中$\gamma$和$\beta$是 network 的参数，在训练过程中被学习到的。如下图所示：

为什么要加上$\beta $和$\gamma$？

有一种猜测是，做 normalization 以后feature的平均就一定是 0，这可能会给 network 一些限制，也许这个限制会带来什麼负面的影响。所以在训练的时候，将$\beta $和$\gamma$作为训练参数，重新调整其分布，让它的 hidden layer 的 output平均不是 0 。

如果是这样，那可能又会问：上一步做Batch Normalization 就是要让每一个不同的 dimension的 range 都是一样的，现在如果做这一步，不是又让 dimension 的分布不一样了吗？

答案是：确实有可能。以我们**在初始的时候，将$\beta $内的元素都设置为1，$\gamma$内的元素都设置为0。\ast \ast 于是network在一开始训练的时候,每一个dimension的分布,是比较接近的，也许训练到后来，已经找到一个比较好的errorsurface，走到一个比较好的地方以后，再慢慢调整$\beta $和$\gamma$。

batch normalization for testing/inference

之前说的都是training的时候要做什么，在testing（inference）的时候，想用batch normalization会有什么问题呢？

batch normalization需要一个batch的数据计算$\mu$和$\sigma$，在testing的时候，首先遇到的问题是，可能输入不够一个batch size，因为在工程上不可能等数据攒到一个batch size才开始计算输出。

也就是可能根本就不是一个batch的输入，应该怎么获得$\mu$和$\gamma$呢？

在实际操作中，如果是PyTorch 的话，Batch Normalization 在 testing 的时候，其使用的$\mu$和$\gamma$是通过：如果training的时候有做 Batch Normalization 的话，在 training 的时候，每一个 batch 计算出来的$\mu$和$\sigma$ 都计算moving average，然后得到平均值（$\bar{\mu }$和$\bar{\sigma }$），将这两个值作为testing的$\mu$和$\sigma$。如下图所示。

moving average的计算过程是：每一次取一个 batch 出来的时候,就会算一个${\mu }^1$，取第二个 batch 出来的时候算${\mu }^2$ ,一直到取第 t 个 batch 出来的时候算${\mu }^t$，利用${\mu }^1...{\mu }^{t-1}$算一个平均值得到$\bar{\mu }$然后结合一个超参数$p$更新$\bar{\mu }$。

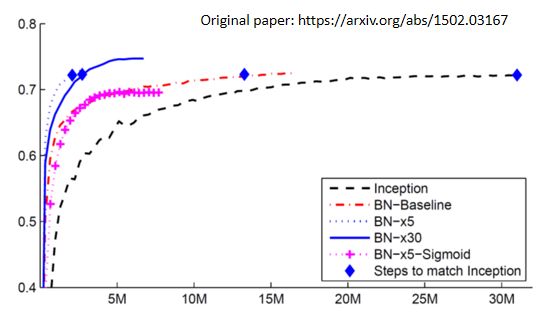
看看加了batch normalization的训练效果：横轴是训练过程，纵轴是在验证集上的精度。

1. 训练速度变快，收敛速度变快；
2. 更好训练（sigmoid比较难训练，但是加入batch normalization后成功训练起来了）；
3. 如果做 Batch Normalization 的话,error surface 会比较平滑 比较容易训练，所以可以把 learning rate 设大一点，（但是这里有个问题是：learning rate 设 30 倍的时候比 5 倍差，作者也没有解释为什么）。

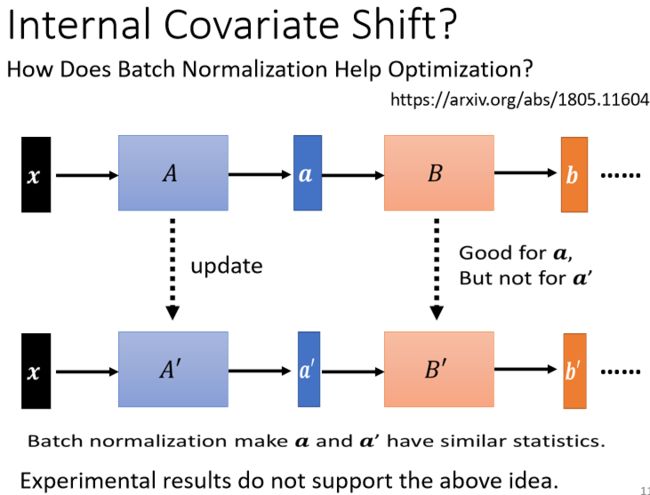
internal covariate shift

在原始的 Batch Normalization那篇 paper 作者提出来一个概念,叫做 internal covariate shift。（友情先提醒这个猜测已经被推翻了）

其中covariate shift是本身存在的概念：训练集和预测集样本分布不一致的问题就叫做“covariate shift”现象。

internal covariate shift指的是：当我们在计算 B,update 到 B′ 的 gradient 的时候，这个时候前一层的参数是 A （或者说是前一层的 output 是a），那当前一层从 A 变成 A′ 的时候,它的 output 就从 a 变成 a′ 。但是我们计算这个 gradient 的时候,我们是根据这个 a 算出来的，所以这个 update 的方向,也许它适合用在 a 上,但不适合用在 a′ 上面。

所以如果每次都有做 normalization,可能就会让 a 跟 a′ 的分布比较接近,也许这样就会对训练有帮助。

如下图所示：

但是！

有一篇 paperHow Does Batch Normalization,Help Optimization就推翻了internal covariate shift 的这一个观点。

作者从各种各样的角度说明internal covariate shift它不一定是 training network 的时候的一个问题，且Batch Normalization会比较好不一定是因为解决了 internal covariate shift问题。

作者通过比较训练时a 分布的变化发现：

1. 不管有没有做 Batch Normalization,它的变化都不大；
2. 就算是变化很大，对 training 也没有太大的伤害；
3. 不管你是根据 a 算出来的 gradient,还是根据 a′ 算出来的 gradient,方向都差不多。

这篇 How Does Batch Normalization,Help Optimization 论文中从实验上、也从理论上至少支持了 Batch Normalization,可以改变 error surface,让 error surface 比较不崎岖这个观点。并且说：如果我们要让 network的error surface 变得比较不崎岖，不一定要做 Batch Normalization，还有很多其他的方法（作者也试了一些其他的方法，见原文实验），batch normalization只是一个serendipitous（意料之外的发现），恰好work了而已。

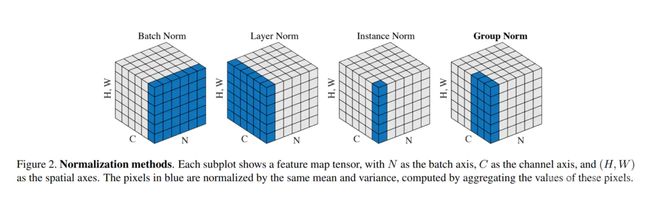
其他normalization的方法

主要包括以下几种方法：BatchNorm（2015年）、LayerNorm（2016年）、InstanceNorm（2016年）、GroupNorm（2018年）。这几个方法在之前总结Transformer时简单总结过了，可以参考：Transformer相关——（6）Normalization方式

normalization方法和paper原文如下：

Batch Renormalization

Layer Normalization

Instance Normalization

Group Normalization

Weight Normalization

Spectrum Normalization

参考资料

[李宏毅深度学习2021春季笔记](https://unclestrong.github.io/DeepLearning_LHY21_Notes/Notes_html/05_Batch and Momentum.html)

(强推)李宏毅2021春机器学习课程