课程向：深度学习与人类语言处理 ——李宏毅，2020 (P8)

Alignment Questions in HMM，CTC，RNN-T

李宏毅老师2020新课深度学习与人类语言处理课程主页：
http://speech.ee.ntu.edu.tw/~tlkagk/courses_DLHLP20.html
视频链接地址：
https://www.bilibili.com/video/BV1RE411g7rQ
课件ppt已上传至资源，可免费下载使用

对于语音辨识系统的三个模型HMM 、CTC、RNN-T，我们将解决四个问题，并做三个模型的总结比较。

前言

在上两篇P5、P6中，我们明晰了HMM、CTC、RNN-T的模型细节，但都遇到了同样的问题，那就是Encoder生成的hidden state(或HMM的state)与token间的长度不等，导致的alignment的问题。
在此，我们提出了4个问题：

1. 问题1：怎么穷举所有可能的alignments？ （P7已解答）
2. 问题2：怎么把所有的alignments加起来？
3. 问题3：怎么做训练？HMM用的是GMM我们不管它。而CTC，RNN-T用的是gradient descent，我们该怎么计算将这些alignment加起来的偏微分？
4. 问题4：怎么做Decoding呢？怎么最优化这个P(Y|X)呢？

下面让我们来解决剩下的三个问题，注意，本节有一定挑战性。

---

I Q2：如何累加alignments代表的概率

以下计算都以RNN-T为例，CTC、HMM同理

1 一条路径的概率计算

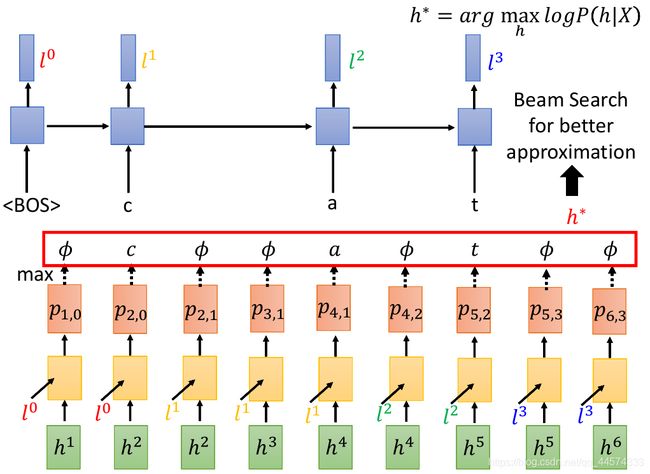
在算所有的alignments的总和之前，我们先来算一条路径的一个alignment的概率，如上图所示。
  我们选取一条alignment ， h = c a t ，我们要怎么计算给acoustic feature x1-6 来产生这个这个alignment h的几率呢？
首先，先计算 在句首的几率 P（|X），再计算 给了 产生 c的几率 P(c|X,)，再计算已产生 c 后生成 的几率 P（|X， c），…，依次类推，直到计算到P(|X,cat)。最终将这些几率累乘，便是这一个路径也就是一个alignment的几率。

2 模型中如何具体计算上述的 类似P(|X)的概率呢？

对于RNN-T而言，模型会先读取第一个acoustic feature h1(经过encoder的x1)，同时RNN-T另外训练了一个RNN，这个RNN会把decoder产生出来的token当作输入(注意，忽略)，生成l去影响RNN-T接下来的输入，正如上图，左上角就是这个单独训练的RNN。
  具体而言，对于上图的h的概率计算：
    首先，另外训练的RNN(上图左上角，蓝色框框)因为一开始没有token故输入初始token (begin of sentence)，产生一个vector l0(红色)，接下来把从encoder来的h1(代表第一个acoustic feature)和l0输入到Decoder里面，Decoder产生一个probability distribution 概率分布 （用p1,0表示，第一个下标1代表由第一个acoustic feature，第二个下标0代表decoder产生0个token），则P(|X)便是p1,0里面的概率。接下来我们要计算P(c|X,)，在decoder 产生 的时候：对于左上角的RNN是没有影响的，故还是RNN给decoder的还是l0； 但对decoder而言，一旦生成 就代表decoder要处理下一个 acoustic feature 故输入h2，同样地，decoder产生一个probability distribution，其中c的概率便是P(c|X,)，依次类推，并把这些概率累乘便得到了P(h|X)。
  总而言之，计算P(h|X)中的每一项就是按步查找按照对应的probability distribution，对本例而言，也就是 在p1,0的几率，c在p2,0的几率， 在p2,1的几率，…， 在p6,3的几率 的累乘（上上图的路径累乘），就是这个alignment的几率。

3 RNN-T中单独训练的RNN怎样对训练有帮助？

RNN-T特别之处，就在于它特别把token和token之间的关系独立用另外一个RNN来表示，而这个RNN是忽略的，那这样做到底对训练有什么好处呢？

上图表格中的每一个格都对应到一个固定的概率的distribution，如上图的蓝点(x4,a)代表p4,2 （而这个p4,2正如上文所讲，第一个下标代表由第几个acoustic feature产生，第二个下标代表decoder已经产生了几个token）因此 这里的p4,2指的是读到x4的acoustic feature，已经产生了2个token c和a，并已经放到了单独训练的RNN里产生l2。因此，

  关键点：每个格子代表的distribution不受到如何走到这个格子所影响。

就比如我们走到p4,2这个格子有很多种走法，但一走到这个格子，这个格子代表的distribution是固定的。

至此，请思考：为什么这里的每个格子代表的distribution是不受路径影响的？
  回答：具体而言，如这个p4,2，参见2的图示，它代表它由第4个acoustic feature h4 和已经产生了两个token (c a)并输入到单独训练的RNN产生的l2决定。对于h4它只与已经产生的的个数有关，l2只与已经产生的token数目有关。这个单独训练的RNN是独立的，它只处理token，故无论在什么位置，对于顺序固定的token，它的输出都是一样的。

4 怎样累加所有alignments呢？

既然我们已经知道如何计算一条路径(即一个alignment的几率)，那我们该怎样求得所有alignments的总和呢？

${\alpha }_{i,j}$

在这里，我们首先定义${\alpha }_{i,j}$，代表考虑所有已经读了 i 个acoustic feature 和 输出 j 个token，我们把这些分数统统加总起来就是${\alpha }_{i,j}$。
  而上面表格中每一个格子也同样对应一个${\alpha }_{i,j}$，如${\alpha }_{4,2}$格子，把所有读过4个acoustic feature且输出2个token的路径统统找出来，将概率累加，如图所示的殊途同归的路线。
而这个${\alpha }_{4,2}是由{\alpha }_{4,1}和{\alpha }_{3,2}产生$，计算式为：
$${\alpha }_{4,2}={\alpha }_{4,1}\ast p_{4,1}(a)+{\alpha }_{3,2}\ast p_{3,2}(\varphi )$$
而其中$p_{4,1}(a)和p_{3,2}(\varphi )$是可由固定的distribution的概率得到，至此${\alpha }_{i,j}$可依次计算得到，而最右下角的${\alpha }_{i,j}$就是所有alignments的总和（用dynamic programming方法从左上一直算到右下即可）。

至此，我们已经能够计算
$P_{\theta }(Y|X)={\sum }_{h\in align(Y)}P(h|X)$

II Q3： 如何计算累加的alignments概率对训练参数的偏微分

综上，我们已经知道RNN-T的参数要怎么计算$P_{\theta }(Y|X)$，那么在训练中我们的目标是
  假设给一段声音讯号x和人工标注的对应文字$\hat{Y}$，我们希望找到参数$\theta$使得$P_{\theta }(\hat{Y}|X)$的概率最越大越好。而使用深度学习方法，我们会用gradient descent的方法来优化参数。
要做梯度下降，我们就必须要计算参数$\theta$对$P_{\theta }(Y|X)$的偏微分：

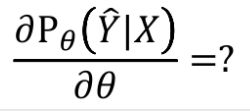
而对于$P(\hat{Y}|X)$是由所有可能的alignment组成的，如下图，由这些几率相乘以后相加。


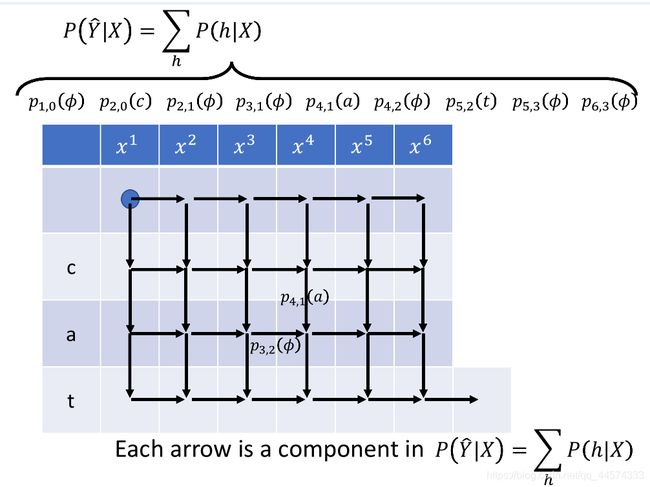
正是这些参数影响了每个格子产生 token 或 的几率，最终影响了$P_{\theta }(\hat{Y}|X)$，以同样可以知道$P_{\theta}(\hat{Y}|X)对 $\theta$ 的偏微分也可以通过这些路径求得。

根据微分公式的分布，亦即，如下图：

对每一项的微分都可以分步成两个部分的乘积，让我们先看第一项第一部分的微分计算方式

第一部分

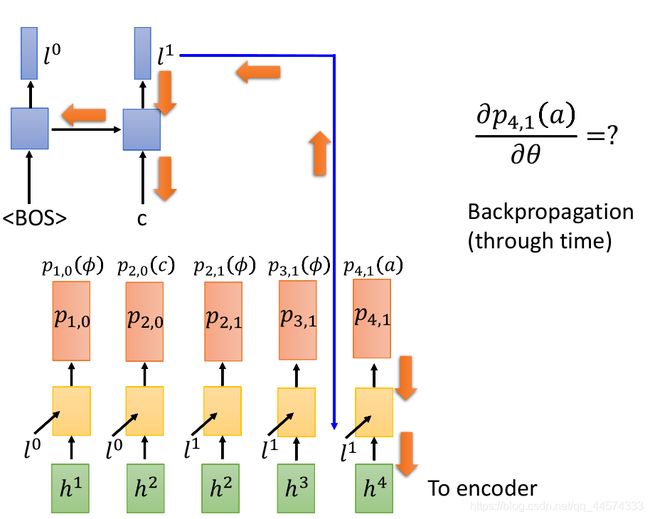
以$p_{4,1}(a)对\theta$的偏微分作为例子，如上图，我们只需使用Backpropagation(因为用RNN，故要through time)，先初始化参数产生$p_{4,1}$，接下来Bp更新参数，和训练一般的神经网络是一样的。
第一项的第一部分已可以求得。

第二部分

接下来，我们要计算$p(\hat{Y}|X)对p_{4,1}(a)$的偏微分

其中$p(\hat{Y}|X)$是由很多alignment组成的，我们先把它们分成两类，一类是有$p_{4,1}(a)$，另外一类是没有$p_{4,1}(a)$，然后分别加起来。接下来，我们对这两类可以分别做偏微分并加和，而第二类不包含$p_{4,1}(a)$故偏微分为0；第一类由$p_{4,1}(a)$ x other组成，偏微分后只剩other，而这个other可以写成$\frac{p(h|X)}{p_{4,1}(a)}$，提出$p_{4,1}(a)$只剩$P(h|X)$。

${\beta }_{i,j}$

那么，我们该怎么计算${\sum }_{h|with{p}_{4,1}(a)}P(h|X)$呢，至此，我们引入一个新的符号$\beta$,刚才我们已经知道怎么算$\alpha$了，这个${\beta }_{i,j}$和${\alpha }_{i,j}$很像，只不过它代表的是从i,j点到终点的alignments的概率和，示例如下图，算法和${\alpha }_{i,j}$一样。

至此${\sum }_{h|with{p}_{4,1}(a)}P(h|X)$ 可以写成 ${\alpha }_{4,1}{p}_{4,1}(a){\beta }_{4,2}$ ,将$p_{4,1}(a)$约掉：
    第一项的第二部分只剩${\alpha }_{4,1}{\beta }_{4,2}$，这两者都可求得
至此，第一项的偏微分已经求得了，剩余项一样的算法。

IV Q4：训练好模型该怎么做Decode，怎么最优化P(Y|X)

在我们已经知道怎么通过Gradient descent更新参数训练模型后，训练好模型后我们该怎么做测试，即Decoding呢？

1 Decoding

我们现在有了模型的参数，所以我们可以算出$P(Y|X)$，接下来在语音辨识的时候，声音讯号给定了即X，要找出Y，使得$P(Y|X)$最大，这个使得$P(Y|X)$最大的Y便是语音辨识的结果。

理想上：找一个Y，使得$\sum P(h|X)$最大
但现实中 : 使得$P(Y|X)$最大是比较困难的，要穷举所有的Y算出$P(Y|X)$，在实作上，有一种近似的方法，就是我们把$\sum P(h|X)$替换成$\max P(h|X)$，就是将align(Y)范围内的h的求和替换成范围内使得概率最大的h

我们不把每一个Y所有的alignments的分数加起来，我们只比每一个Y，它范围内h分数最高的alignment，得到该h后，反向alignment得到我们预测的$\hat{Y}$

2 怎么找最大的alignment

两种方法：

1. 把decoder产生的每一个distribution里面概率最大的token拿出来，当作最大的alignment(Greedy)
2. Beam Search

这两种方法在P4 Attend里有详细讲解，不再阐述。

V Summary

这个RNN-T training部分其实是比较困难的，如果前面讲的东西你没有听的很懂，那没有关系，你并不孤单

如果你对RNN-T training部分没有看懂，至少你可以看一下这三个常用模型的比较。

1. Decoder部分，LAS会考虑前面的timestamp已经产生的token，而CTC不会考虑前面的timestamp已经产生的token，RNN-T有考虑前面的timestamp已经产生的token。
2. Alignment部分，LAS并不明确考虑Alignment的问题，LAS用attention的机制来找出语音和文字之间的关系，但CTC和RNN-T要考虑Alignment的问题。
3. Training部分，LAS”硬train一发“，而CTC、RNN-T训练是比较麻烦的，必须要穷举并加起来所有的alignment
4. On-line部分，对语音辨识很重要的一项便是 实时辨识，而LAS做不到，但CTC和RNN-T可以做到。(pixel 的语音辨识用的就是RNN-T)