❤️《画解数据结构》九张动图，画解顺序表❤️

本文已收录于专栏 《画解数据结构》

零、前言

  这篇文章，作者将用 「 七张动图 」 来阐述一种最基础的顺序结构

「 顺序表 」
  相信看我文章的大多数都是 「 大学生 」，能上大学的都是 「 精英 」，那么我们自然要 「 精益求精 」，如果你还是 「 大一 」，那么太好了，你拥有大把时间，当然你可以选择 「 刷剧 」，然而， 「 学好算法 」，三年后的你自然 「 不能同日而语 」。
  那么这里，我整理了 「 几十个基础算法 」 的分类，点击开启：

《算法入门指引》
  如果链接被屏蔽，或者有权限问题，可以私聊作者解决。大致题集一览：





  为了让这件事情变得有趣，以及 「 照顾初学者 」，目前题目只开放最简单的算法 「 枚举系列 」 （包括：线性枚举、双指针、前缀和、二分枚举、三分枚举），当有 一半成员刷完 「 枚举系列 」 的所有题以后，会开放下个章节，等这套题全部刷完，你还在群里，那么你就会成为 「 夜深人静写算法 」专家团 的一员。
  不要小看这个专家团，三年之后，你将会是别人 望尘莫及 的存在。如果要加入，可以联系我，考虑到大家都是学生， 没有「 主要经济来源 」，在你成为神的路上， 「 不会索取任何 」。

放心成神！自律使你自由！
C语言免费动漫教程，和我一起打卡！ 《光天化日学C语言》
LeetCode 太难？先看简单题！ 《C语言入门100例》
数据结构难？不存在的！ 《画解数据结构》
闭关刷 LeetCode，剑指大厂Offer！ 《算法入门指引》
LeetCode 太简单？算法学起来！ 《夜深人静写算法》

  说了这么多，学习之前，我们来看下 「 枚举系列 」 中几个经典的算法，将算法之前，我会介绍一下 C语言 中一种最简单的数据结构，即 数组。首先来看，内容提要：

一、概念

1、顺序存储

  顺序存储结构，是指用一段地址连续的存储单元依次存储线性表的数据元素。

2、存储方式

  在编程语言中，用一维数组来实现顺序存储结构，在C语言中，把第一个数据元素存储到下标为 0 的位置中，把第 2 个数据元素存储到下标为 1 的位置中，以此类推。

3、长度和容量

  数组的长度指的是数组当前有多少个元素，数组的容量指的是数组最大能够存放多少个元素。如果数组元素大于最大能存储的范围，在程序上是不允许的，可能会产生意想不到的问题，实现上是需要规避的。

  如上图所示，数组的长度为 5，即红色部分；容量为 8，即红色 加 蓝色部分。

4、数据结构定义

#define MAXN 1024
#define DataType int        // (1)

struct SeqList {
     
    DataType data[MAXN];    // (2)
    int length;             // (3)
}; 

• $(1)$ 数组类型为DataType，定义为int；
• $(2)$ SeqList定义的就是一个最多存放MAXN个元素的数组，MAXN代表数组容量；
• $(3)$ length代表数组长度，即当前的元素个数。

二、常用接口实现

1、只读接口

1）索引

  索引 就是通过 数组下标 寻找 数组元素 的过程。C语言实现如下：

DataType SeqListIndex(struct SeqList *sq, int i) {
     
    return sq->data[i];          // (1)
}

• $(1)$ 调用方需要注意 $i$ 的取值必须为非负整数，且小于数组最大长度。否则有可能导致异常，引发崩溃。
• 索引的算法时间复杂度为 $O(1)$。
  

2）查找

  查找 就是通过 数组元素 寻找 数组下标 的过程，是索引的逆过程。
  对于有序数组，可以采用 二分 进行查找，时间复杂度为 $O(lo{g}_{2}n)$；对于无序数组，只能通过遍历比较，由于元素可能不在数组中，可能遍历全表，所以查找的最坏时间复杂度为 $O(n)$。
  简单介绍一个线性查找的例子，实现如下：

DataType SeqListFind(struct SeqList *sq, DataType dt) {
     
    int i;
    for(i = 0; i < sq->length; ++i) {
      // (1)
        if(sq->data[i] == dt) {
     
            return i;                 // (2)
        }    
    }
    return -1;                        // (3)
}

• $(1)$ 遍历数组元素；
• $(2)$ 对数组元素 和 传入的数据进行判等，一旦发现相等就返回对应数据的下标；
• $(3)$ 当数组遍历完还是找不到，说明这个数据肯定是不存在的，直接返回 $-1$。
  

3）获取长度

  获取 数组的长度 指的是查询当前有多少元素。可以直接用结构体的内部变量。C语言代码实现如下：

DataType SeqListGetLength(struct SeqList *sq) {
     
    return sq->length; 
}

2、可写接口

1）插入

  插入接口定义为：在数组的第 $k$ 个元素前插入一个数 $v$。由于数组是连续存储的，那么从 $k$ 个元素往后的元素都必须往后移动一位，当 $k=0$ 时，所有元素都必须移动，所以最坏时间复杂度为 $O(n)$。C语言代码实现如下：

int SeqListInsert(struct SeqList *sq, int k, DataType v) {
     
    int i;
    if(sq->length == MAXN) {
     
        return 0;                        // (1) 
    } 
    for(i = sq->length; i > k; --i) {
     
        sq->data[i] = sq->data[i-1];     // (2) 
    }
    sq->data[k] = v;                     // (3) 
    sq->length ++;                       // (4) 
    return 1;                            // (5) 
}

• $(1)$ 当元素个数已满时，返回 $0$ 代表插入失败；
• $(2)$ 从第 $k$ 个数开始，每个数往后移动一个位置，注意必须逆序；
• $(3)$ 将第 $k$ 个数变成 $v$；
• $(4)$ 插入了一个数，数组长度加一；
• $(5)$ 返回 $1$ 代表插入成功；

2）删除

  插入接口定义为：将数组的第 $k$ 个元素删除。由于数组是连续存储的，那么第 $k$ 个元素删除，往后的元素势必要往前移动一位，当 $k=0$ 时，所有元素都必须移动，所以最坏时间复杂度为 $O(n)$。C语言代码实现如下：

int SeqListDelete(struct SeqList *sq, int k) {
     
    int i;
    if(sq->length == 0) {
     
        return 0;                        // (1) 
    } 
    for(i = k; i < sq->length - 1; ++i) {
     
        sq->data[i] = sq->data[i+1];     // (2) 
    } 
    sq->length --;                       // (3) 
    return 1;                            // (4)  
}

• $(1)$ 返回0代表删除失败；
• $(2)$ 从前往后；
• $(3)$ 数组长度减一；
• $(4)$ 返回1代表删除成功；

三、优缺点

1、优点

  1）无须为表示表中元素逻辑关系而增加额外的存储空间；
  2）随机存取元素时可以达到 $O(1)$，效率高；

2、缺点

  1）插入和删除时需要移动大量元素；
  2）必须一开始就确定存储空间的容量；

四、数组相关算法

1、线性枚举

1）问题描述

  给定一个长度为 $n(1\le n\le 10^5)$ 的整型数组，求所有数组元素中的其中的最小值。

2）动图演示

3）示例说明

  蓝色的数据代表的是数组数据，红色的数据代表当前枚举到的数据，这样就可以遍历所有的数据进行逻辑处理了。

4）算法描述

  遍历数组，进行条件判断，条件满足则执行逻辑。这里的条件就是 枚举到的数 是否小于 当前最小值，执行逻辑为 将 当前枚举到的数 赋值给 当前最小值；

5）源码详解

int findMin(int* nums, int numsSize){
     
    int i, min = 100000;
    for(i = 0; i < numsSize; ++i) {
          // (1)
        if(nums[i] < min) {
                  // (2)
            min = nums[i];
        }
    }
    return min;                         // (3)
}

• $(1)$ 遍历数组中所有的数；
• $(2)$ 如果 当前枚举到的数 比记录的变量min小，则将它赋值给min；否则，不做任何处理；
• $(3)$ 最后，min中存储的就是整个数组的最小值。

2、前缀和差分

1）问题描述

  给定一个 $n(n\le 10^5)$ 个元素的整型数组 $a_i$，再给出 $m(m\le 10^5)$ 次询问，每次询问是一个区间 $[l,r]$，求 $h(l,r)={\sum }_{k=l}^r{a}_k$

2）动图演示

3）样例分析

  如上图所示，只需要记录一个前缀和，然后就可以通过一次减法将区间的值计算出来。时间复杂度 $O(1)$。这种就是差分的思想。

4）算法描述

  第一个枚举，利用一个数组sum，存储前 $i$ 个元素的和。
  第二个枚举，读入 $m$ 组数据 $l,r$，对每组数据，通过 $O(1)$ 获取答案，即 $su{m}_r-su{m}_{l-1}$。

5）源码详解

int sum[maxn];
int* prefixSum(int* nums, int numsSize, int m, int *l, int *r){
     
    int i;
    int *ret;
    for(i = 0; i < numsSize; ++i) {
     
        sum[i] = nums[i];
        if(i) 
            sum[i] += sum[i-1];                 // (1) 
    }
    ret = (int *) malloc( m * sizeof(int) );    // (2) 
    for(i = 0; i < m; ++i) {
     
    	int leftsum = l==0? 0 : sum[l-1];       // (3) 
    	int rightsum = sum[r];
    	ret[i] = rightsum - leftsum;            // (4) 
    }
    return ret;
}

• $(1)$ 计算前缀和；
• $(2)$ 需要返回的数组；
• $(3)$ 这里是为了防止数组下标越界；
• $(4)$ 核心 $O(1)$ 的差分计算；

3、双指针

1）问题描述

  给定一个长度为 $n(1\le n\le 10^7)$ 的字符串 $s$，求一个最长的满足所有字符不重复的子串。

2）动图演示

3）样例说明

  维护两个指针 $i$ 和 $j$，区间 $[i,j]$ 内的子串，应该时刻保持其中所有字符不重复，一旦发现重复字符，就需要自增 $i$（即执行 $i=i+1$）；否则，执行 $j=j+1$，直到 $j$ 不能再增加为止。
  过程中，记录合法情况下 $j-i+1$ 的最大值。

4）算法描述

  如上文所述，这种利用问题特性，通过两个指针，不断调整区间，从而求出问题最优解的算法就叫 “尺取法”，由于利用的是两个指针，所以又叫 “双指针” 算法。
  这里 “尺” 的含义，主要还是因为这类问题，最终要求解的都是连续的序列（子串），就好比一把尺子一样，故而得名。

算法描述如下：
  1）初始化 $i=0$, $j=i-1$，代表一开始 “尺子” 的长度为 0；
  2）增加 “尺子” 的长度，即 $j=j+1$；
  3）判断当前这把 “尺子” $[i,j]$ 是否满足题目给出的条件：
    3.a）如果不满足，则减小 “尺子” 长度，即 $i=i+1$，回到 3）；
    3.b）如果满足，记录最优解，回到 2）；

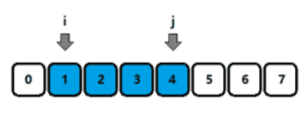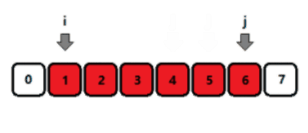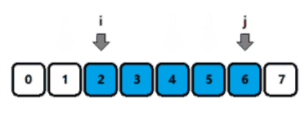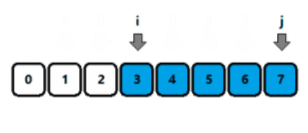
• 上面这段文字描述的比较官方，其实这个算法的核心，只有一句话： 满足条件时， $j$++；不满足条件时， $i$++；
• 如图所示，当区间 $[i,j]$ 满足条件时，用蓝色表示，此时 $j$ 自增；反之闪红，此时 $i$ 自增。
  

5）源码详解

int getmaxlen(int n, char *str, int& l, int& r) {
     
    int ans = 0, i = 0, j = -1, len;   // 1)
    memset(h, 0, sizeof(h));           // 2)
    while (j++ < n - 1) {
                   // 3)
        ++h[ str[j] ];                 // 4)
        while (h[ str[j] ] > 1) {
           // 5)
            --h[ str[i] ];
            ++i;
        }
        len = j - i + 1;              
        if(len > ans)                  // 6)
            ans = len, l = i, r = j;
    }
    return ans;
}

• 1）初始化 i = 0, j = -1，代表 $s[i:j]$ 为一个空串，从空串开始枚举；
• 2）需要维护一个哈希表，哈希表记录的是当前枚举的区间 $s[i:j]$ 中每个字符的个数；
• 3）只推进子串的右端点；
• 4）在哈希表中记录字符的个数；
• 5）当 h[ str[j] ] > 1满足时，代表出现了重复字符str[j]，这时候左端点 $i$ 推进，直到没有重复字符为止；
• 6）记录当前最优解的长度 j - i + 1，更新；
• 这个算法执行完毕，我们就可以得到最长不重复子串的长度为 $ans$，并且 $i$ 和 $j$ 这两个指针分别只自增 $n$ 次，两者自增相互独立，是一个相加而非相乘的关系，所以这个算法的时间复杂度为 $O(n)$ 。

4、二分枚举

1）问题描述

  给定一个 $n(n\le 10^6)$ 个元素的有序整型数组和一个 $target$ 值，求在 $O(lo{g}_{2}n)$ 的时间内找到值为 $target$ 的整型的数组下标，不存在则返回 -1。

2）动图演示

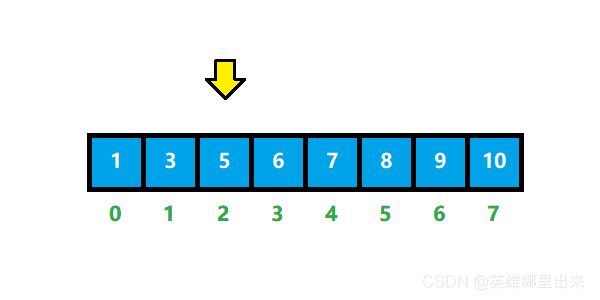
3）样例说明

  需要找值为 $5$ 的这个元素。
  黄色箭头 代表都是左区间端点 $l$，红色箭头 代表右区间端点 $r$。蓝色的数据为数组数据，绿色的数字代表的是数组下标，初始化 $l=0$，$r=7$，由于数组有序，则可以直接折半，令 $mid=(l+r)/2=3$，则 $5$ 一定落入区间 $[0,3]$，这时候令 $r=3$，继续执行，直到 $l>r$ 结束迭代。
  最后，当 $mid=2$ 时，找到数据 5。

4）算法描述

  a）令初始情况下，数组下标从 0 开始，且数组长度为 $n$，则定义一个区间，它的左端点是 $l=0$，右端点是 $r=n-1$；
  b）生成一个区间中点 $mid=(l+r)/2$，并且判断 $mid$ 对应的数组元素和给定的目标值的大小关系，主要有三种：
    b.1）目标值 等于 数组元素，直接返回 $mid$；
    b.2）目标值 大于 数组元素，则代表目标值应该出现在区间 $[mid+1,r]$，迭代左区间端点：$l=mid+1$；
    b.3）目标值 小于 数组元素，则代表目标值应该出现在区间 $[l,mid-1]$，迭代右区间端点：$r=mid-1$；
  c）如果这时候 $l>r$，则说明没有找到目标值，返回 $-1$；否则，回到 b）继续迭代。

5）源码详解

int search(int *nums, int numsSize, int target) {
     
    int l = 0, r = numsSize - 1;         // (1)
    while(l <= r) {
                           // (2)
        int mid = (l + r) >> 1;          // (3)
        if(nums[mid] == target) {
        
            return mid;                  // (4)
        }else if(target > nums[mid]) {
     
            l = mid + 1;                 // (5)
        }else if(target < nums[mid]) {
     
            r = mid - 1;                 // (6)
        }
    }
    return -1;                           // (7)
}

• $(1)$ 初始化区间左右端点；
• $(2)$ 一直迭代左右区间的端点，直到 左端点 大于 右端点 结束；
• $(3)$ >> 1等价于除 2，也就是这里mid代表的是l和r的中点；
• $(4)$ nums[mid] == target表示正好找到了这个数，则直接返回下标mid；
• $(5)$ target > nums[mid]表示target这个数在区间 $[mid+1,r]$ 中，所以才有左区间赋值如下：l = mid + 1;
• $(6)$ target < nums[mid]表示target这个数在区间 $[l,mid-1]$ 中，所以才有右区间赋值如下：r = mid - 1;
• $(7)$ 这一步呼应了 $(2)$，表示这不到给定的数，直接返回 -1；

5、三分枚举

  三分枚举 类似 二分枚举 的思想，也是将区间一下子砍掉一块基本完全不可能的块，从而减小算法的时间复杂度。只不过 二分枚举 解决的是 单调性 问题。而 三分枚举 解决的是 极值问题。

6、插入排序

1）问题描述

  给定一个 $n$ 个元素的数组，数组下标从 $0$ 开始，采用「 插入排序 」将数组按照 「升序」排列。

2）动图演示

3）样例说明

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表正在执行 比较 和 移动 的数
■ 的柱形	代表已经排好序的数
■ 的柱形	代表待执行插入的数

  我们看到，首先需要将 「第二个元素」 和 「第一个元素」 进行 「比较」，如果 前者 小于等于 后者，则将 后者 进行向后 「移动」，前者 则执行插入；
  然后，进行第二轮「比较」，即 「第三个元素」 和 「第二个元素」、「第一个元素」 进行 「比较」， 直到 「前三个元素」 保持有序 。
  最后，经过一定轮次的「比较」 和 「移动」之后，一定可以保证所有元素都是 「升序」 排列的。

4）算法描述

整个算法的执行过程分以下几步：
  1） 循环迭代变量 $i=1\to n-1$；
  2） 每次迭代，令 $x=a[i]$，$j=i-1$，循环执行比较 $x$ 和 $a[j]$，如果产生 $x\le a[j]$ 则执行 $a[j+1]=a[j]$。然后执行 $j=j+1$，继续执行 2）；否则，跳出循环，回到 1）。

5）源码详解

#include 

int a[1010];

void Input(int n, int *a) {
     
    for(int i = 0; i < n; ++i) {
     
        scanf("%d", &a[i]);
    }
}

void Output(int n, int *a) {
     
    for(int i = 0; i < n; ++i) {
     
        if(i)
            printf(" ");
        printf("%d", a[i]);
    }
    puts("");
}

void InsertSort(int n, int *a) {
            // (1)
    int i, j; 
    for(i = 1; i < n; ++i) {
     
        int x = a[i];                  // (2)
        for(j = i-1; j >= 0; --j) {
         // (3)
            if(x <= a[j]) {
                 // (4)
                a[j+1] = a[j];         // (5)
            }else
                break;                 // (6)
        }
        a[j+1] = x;                    // (7)
    }
} 

int main() {
     
    int n;
    while(scanf("%d", &n) != EOF) {
     
        Input(n, a);
        InsertSort(n, a);
        Output(n, a);
    }
    return 0;
} 

• $(1)$ void InsertSort(int n, int *a)为 插入排序 的实现，代表对a[]数组进行升序排序。
• $(2)$ 此时a[i]前面的 i-1个数都认为是排好序的，令x = a[i]；
• $(3)$ 逆序的枚举所有的已经排好序的数；
• $(4)$ 如果枚举到的数a[j]比需要插入的数x大，则当前数往后挪一个位置；
• $(5)$ 执行挪位置的 $O(1)$ 操作；
• $(6)$ 否则，跳出循环；
• $(7)$ 将x插入到合适位置；

7、选择排序

1）问题描述

  给定一个 $n$ 个元素的数组，数组下标从 $0$ 开始，采用「 选择排序 」将数组按照 「升序」排列。

2）动图演示

3）样例说明

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表正在执行 比较 的数
■ 的柱形	代表已经排好序的数
■ 的柱形	有两种：1、记录最小元素 2、执行交换的元素

  我们发现，首先从 「第一个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」，和 「第一个元素」 进行 「交换」；
  然后，从 「第二个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」，和 「第二个元素」 进行 「交换」。
  最后，一定可以保证所有元素都是 「升序」 排列的。

4）算法描述

整个算法的执行过程分以下几步：
  1） 循环迭代变量 $i=0\to n-1$；
  2） 每次迭代，令 $min=i$，$j=i+1$；
  3） 循环执行比较 $a[j]$ 和 $a[min]$，如果产生 $a[j]<a[min]$ 则执行 $min=j$。执行 $j=j+1$，继续执行这一步，直到 $j==n$；
  4） 交换 $a[i]$ 和 $a[min]$，回到 1）。

5）源码详解

#include 

int a[1010];

void Input(int n, int *a) {
     
    for(int i = 0; i < n; ++i) {
     
        scanf("%d", &a[i]);
    }
}

void Output(int n, int *a) {
     
    for(int i = 0; i < n; ++i) {
     
        if(i)
            printf(" ");
        printf("%d", a[i]);
    }
    puts("");
}

void Swap(int *a, int *b) {
     
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void SelectionSort(int n, int *a) {
       // (1)
    int i, j;
    for(i = 0; i < n - 1; ++i) {
          // (2)
        int min = i;                 // (3)
        for(j = i+1; j < n; ++j) {
        // (4)
            if(a[j] < a[min]) {
     
                min = j;             // (5)
            }
        }
        Swap(&a[i], &a[min]);        // (6) 
    }
}

int main() {
     
    int n;
    while(scanf("%d", &n) != EOF) {
     
        Input(n, a);
        SelectionSort(n, a);
        Output(n, a);
    }
    return 0;
} 

• $(1)$ void SelectionSort(int n, int *a)为选择排序的实现，代表对a[]数组进行升序排序。
• $(2)$ 从首元素个元素开始进行 $n-1$ 次跌迭代。
• $(3)$ 首先，记录min代表当前第 $i$ 轮迭代的最小元素的下标为 $i$。
• $(4)$ 然后，迭代枚举第 $i+1$ 个元素到 最后的元素。
• $(5)$ 选择一个最小的元素，并且存储下标到min中。
• $(6)$ 将 第 $i$ 个元素 和 最小的元素 进行交换。

8、冒泡排序

1）问题描述

  给定一个 $n$ 个元素的数组，数组下标从 $0$ 开始，采用「 冒泡排序 」将数组按照 「升序」排列。

2）动图演示

3）样例说明

图示	含义
■ 的柱形	代表尚未排好序的数
■ 的柱形	代表正在执行比较的两个数
■ 的柱形	代表已经排好序的数

  我们看到，首先需要将 「第一个元素」 和 「第二个元素」 进行 「比较」，如果 前者 大于 后者，则进行 「交换」，然后再比较 「第二个元素」 和 「第三个元素」 ，以此类推，直到 「最大的那个元素」 被移动到 「最后的位置」 。
  然后，进行第二轮「比较」，直到 「次大的那个元素」 被移动到 「倒数第二的位置」 。
  最后，经过一定轮次的「比较」 和 「交换」之后，一定可以保证所有元素都是 「升序」 排列的。

4）算法描述

整个算法的执行过程分以下几步：
  1） 循环迭代变量 $i=0\to n-1$；
  2） 每次迭代，令 $j=i$，循环执行比较 $a[j]$ 和 $a[j+1]$，如果产生 $a[j]>a[j+1]$ 则交换两者的值。然后执行 $j=j+1$，这时候对 $j$ 进行判断，如果 $j\ge n-1$，则回到 1），否则继续执行 2）。

5）源码详解

#include 

int a[1010];

void Input(int n, int *a) {
     
    for(int i = 0; i < n; ++i) {
     
        scanf("%d", &a[i]);
    }
}

void Output(int n, int *a) {
     
    for(int i = 0; i < n; ++i) {
     
        if(i)
            printf(" ");
        printf("%d", a[i]);
    }
    puts("");
}

void Swap(int *a, int *b) {
     
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

void BubbleSort(int n, int *a) {
                  // (1)
    bool swapped;
    int last = n;
    do {
     
        swapped = false;                     // (2)
        for(int i = 0; i < last - 1; ++i) {
       // (3)
            if(a[i] > a[i+1]) {
                   // (4)
                Swap(&a[i], &a[i+1]);        // (5)
                swapped = true;              // (6)
            }
        }
        --last;
    }while (swapped);
} 

int main() {
     
    int n;
    while(scanf("%d", &n) != EOF) {
     
        Input(n, a);
        BubbleSort(n, a);
        Output(n, a);
    }
    return 0;
} 

• $(1)$ void BubbleSort(int n, int *a)为冒泡排序的实现，代表对a[]数组进行升序排序。
• $(2)$ swapped标记本轮迭代下来，是否有元素产生了交换。
• $(3)$ 每次冒泡的结果，会执行last的自减，所以待排序的元素会越来越少。
• $(4)$ 如果发现两个相邻元素产生逆序，则将它们进行交换。保证右边的元素一定不比左边的小。
• $(5)$ swap实现了元素的交换，这里需要用&转换成地址作为传参。
• $(6)$ 标记更新。一旦标记更新，则代表进行了交换，所以下次迭代必须继续。

---

  关于 「 数组的算法 」 的内容到这里就结束了。
  如果还有不懂的问题，可以 「 通过主页 」找到作者的「 联系方式 」 ，线上沟通交流。

---

  有关《画解数据结构》 的源码均开源，链接如下：《画解数据结构》

---

本文已收录于专栏 《画解数据结构》

  如果你满足如下：
   $(1)$ 有强烈欲望「 想要学好C语言 」的人
   $(2)$ 有强烈欲望「 想要学好C++ 」的人
   $(3)$ 有强烈欲望「 想要学好数据结构 」的人
   $(4)$ 有强烈欲望「 想学好算法 」的人
   $(5)$ 有强烈欲望「 想进大厂 」的人
  如果你满足以上任意一点，那么，我们就是志同道合的人啦！可以联系我免费加入我们团队。

饭不食，水不饮，题必须刷
C语言免费动漫教程，和我一起打卡！ 《光天化日学C语言》
LeetCode 太难？先看简单题！ 《C语言入门100例》
数据结构难？不存在的！ 《画解数据结构》
闭关刷 LeetCode，剑指大厂Offer！ 《算法入门指引》
LeetCode 太简单？算法学起来！ 《夜深人静写算法》