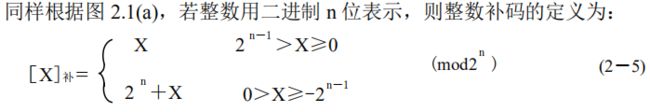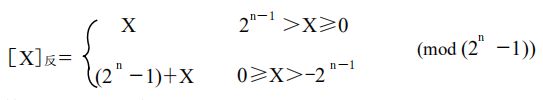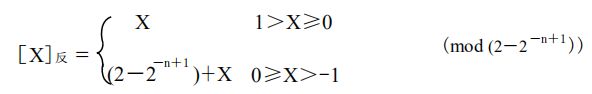计组(二)计算机中的数据表示:原码、补码、反码和移码
文章目录
- 一、概述
-
- 1.进制转换
- 2.无符号数及有符号数
-
- (1) 无符号数
- (2)有符号数
- 3. 定点数与浮点数
-
- (1)定点数
- (2)浮点数
- 二、机器数(二进制数、有符号数)
-
- 0.总结
-
- (1)数的特征
- (2)范围
- (3)自己的计算方式
- 1.原码
-
- (1)整数的原码
- (2)小数的原码
- (3)特性
-
- 零的问题:有两种表示形式+0和-0(符号位)
- 范围
- 2.补码
-
- (1)整数补码
- (2)小数的补码
- (3)特性
-
- 求补运算【链接】
- 简化加减法【链接】
- 可以明显地看出大小
-
- 范围
- 0 的表示是唯一的
- 变形码(双符号位)
- 算术左移、右移
- 3.反码
-
- (1)整数的反码
- (2)小数的反码
- (3)特性
-
- 两种0 的表示
- 负数反码与补码的关系
- 数值范围
- 4.移码
-
- (1)整数的移码
- (2)特性
-
- 移码的零
- 移码与补码的关系
- 移码码值的大小就反映了数值的大小
- 5.题
- 三、浮点数
-
- 1.浮点数的表示
- 2.非规格化浮点数
- 3.规格化的浮点数
-
- (1)什么是规格化的浮点数
- (2)表示范围
- (3)溢出
- 4.规格化浮点数
-
- (1)规格化
- (2)例题
- 四、其他的数据表示
-
- 1.IEEE754
-
- (1)单精度格式(32位)
- (2)双精度格式(64位)
- 2.奇偶校验码
-
- (1)水平奇偶校验
- (2)垂直奇偶校验码
- (2)水平垂直奇偶校验码
- 3.海明码
- 4.循环冗余校验码(CRC 码)
-
- (1)模运算
- (2)CRC 码的编码
- (2)CRC 码的译码校验
一、概述
1.进制转换
https://blog.csdn.net/sandalphon4869/article/details/88298591
2.无符号数及有符号数
(1) 无符号数
没有符号位,则数中的每一位均用来表示数值。
所以,8 位二进制无符号数所表示的数值范围是 0~255, 16 位无符号数的表示范围为 0~65535。
(2)有符号数
带有符号位表示正负,符号位放在有效数字的前面,这样就组成了有符号数。
如4位有符号数范围是-7~7.
3. 定点数与浮点数
(1)定点数
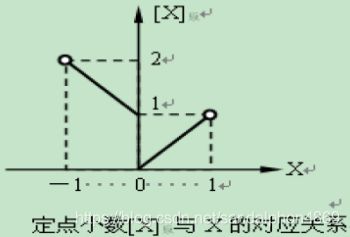
若约定小数点的位置固定不变,则称为定点数。
有两种形式的定点数:定点整数(就是纯整数,小数点定在最低有效数值位之后)和定点小数(就是纯小数,小数点在最高有效数值位之前)。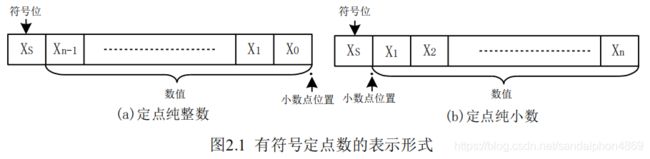
(2)浮点数
小数点位置浮动
二、机器数(二进制数、有符号数)
各种数值数据在计算机中表示的形式称为机器数。机器数对应的实际数值称数的真值。
0.总结
(1)数的特征
符号位
| 机器码 | 0 | 1 |
|---|---|---|
| 原码 | 0正 | 1负 |
| 反码 | 0正 | 1负 |
| 补码 | 0正 | 1负 |
| 移码 | 0负 | 1正 |
零
唯一零:补码(0000…0)、移码(1000…0)
不唯一的零:原码(+0与-0,即0000…0与1000…0)、反码(0000…0与1111…1)
(2)范围
Something Help:
- 1000: 2 4 − 1 = 2 3 = 8 2^{4-1}=2^3=8 24−1=23=8
- 0111: 2 2 + 2 1 + 2 0 = 2 3 = 2 4 − 1 − 1 = 7 2^2+2^1+2^0=2^3=2^{4-1}-1=7 22+21+20=23=24−1−1=7,也可以因为0111+1=1000,那么0111=1000-1= 2 3 − 1 = 7 2^3-1=7 23−1=7
- 0.001: 2 − 3 = 0.125 2^{-3}=0.125 2−3=0.125
- 0.111: 2 − 1 + 2 − 2 + 2 − 3 = 0.875 2^{-1}+2^{-2}+2^{-3}=0.875 2−1+2−2+2−3=0.875,也可以因为0.111+0.001=1.000,那么0.111=1.000-0.001= 1 − 2 − 3 = 0.875 1-2^{-3}=0.875 1−2−3=0.875
原码 n 位(包括一位符号位):
- 整数数值范围分别为:1111…1~0111…1,即 − ( 2 n − 1 - 1 ) ~ + ( 2 n − 1 - 1 ) -(2^{n-1}-1)~+(2^{n-1}-1) −(2n−1-1)~+(2n−1-1)。0111…1是 ( 2 n − 1 - 1 ) (2^{n-1}-1) (2n−1-1),最小负数是加个负号, − ( 2 n − 1 - 1 ) -(2^{n-1}-1) −(2n−1-1)
- 纯小数所能表示的:1.111…1~0.111…1,即 − ( 1 − 2 − ( n − 1 ) ) ~ + ( 1 - 2 − ( n − 1 ) ) {-(1-2^{-(n-1)})~+(1-2^{-(n-1)}}) −(1−2−(n−1))~+(1-2−(n−1))。0.111…1是 1 − 2 − ( n − 1 ) 1-2^{-(n-1)} 1−2−(n−1),最小负数是加个负号, − ( 1 − 2 − ( n − 1 ) ) -(1-2^{-(n-1)}) −(1−2−(n−1))
补码 n 位(包括一位符号位):
- 整数数值范围分别为:1000…0~0111…1,即 − 2 n − 1 ~ + ( 2 n − 1 − 1 ) -2^{n-1} ~ +( 2^{n-1}-1) −2n−1~+(2n−1−1)。最大正整数同原码,而且负数可以取到下限 − 2 n − 1 -2^{n-1} −2n−1。
- 小数数值范围分别为:1.000…0~0.111…1,即 − 1 ~ + ( 1 - 2 − ( n − 1 ) ) -1~+(1-2^{-(n-1)}) −1~+(1-2−(n−1))。最大正小数同原码,而且负数可以取到下限-1。
反码 n 位(包括一位符号位):
正数的反码等于原码,负数的反码是对应正数原码的全部取反。那么表示范围同原码。
- 整数数值范围分别为:1000…0~0111…1
- 小数数值范围分别为:1.000…0~0.111…1
移码 n 位(包括一位符号位):
移码是补码的符号位取反,那么范围同补码。
- 整数数值范围分别为:0000…0~1111…1
- 小数数值范围分别为:0.000…0~1.111…1
(3)自己的计算方式
正整数
[x]原= [x]反=[x]补
[x]移=[x]补码的符号位取反
负数
因为求补运算
-
正推
真值→原码(符号位是1)
真值→负数对应的正数的原码→补码(从右往左,第一个1左边全部取反)
真值→负数对应的正数的原码→反码(包据符号位全部取反获得)
真值→负数对应的正数的原码→补码(从右往左,第一个1左边全部取反)→移码 -
反推
原码→真值
补码→负数对应的正数的原码(从右往左,第一个1左边全部取反)→真值
反码→负数对应的正数的原码(包据符号位全部取反获得)→真值
移码→补码→负数对应的正数的原码(从右往左,第一个1左边全部取反)→真值
整数补位增
正数:都是次高位补0
如真值3(011)→00011(原码)→00011(补码)→00011(反码)
移码(111)→(10011)
负数:
- 原码:负数次高位补0
- 补码:负数次高位补1
- 反码:负数次高位补1
- 移码:负数次高位补1
如:真值-3
原码:111→10011
补码:101→11101
反码:100→11100
移码:001→01101
整数补位删
正数:把符号位和符号位右边第一个1之间的0都删掉。
如真值3→00011(原码)→00011(补码)→00011(反码)→(011)
移码(10011)→(111)
负数:
- 原码:把符号位和符号位右边第一个1之间的0都删掉。(删去补的0)
- 补码:把符号位和符号位右边第一个0之间的1都删掉。(删去补的1)
- 反码:把符号位和符号位右边第一个0之间的1都删掉。(删去补的1)
- 移码:把符号位和符号位右边第一个0之间的1都删掉。(删去补的1)
如:真值-3
原码:10011→111
补码:11101→101
反码:11100→100
移码:01101→001
特殊情况
-
注意原码的+0和-0
-
【求-8的的八位补码】
8的原码(0000 1000)→-8的的八位补码(1111 1000) -
【1111 1000是补码,则对应真值是?】
补码→正数的原码(0000 1000)→真值-8 -
【求-8的的四位补码】
8的原码(01000)→-8的的八位补码(11000)→补位删(1000) -
【1000是补码,则对应真值是?】
补码→正数的原码(1000),出错
补码→补位增(11000)→正数的原码(0 1000)→真值-8
1.原码
原码是机器数中最简单的一种表示形式。
(1)整数的原码
表示方法一:由真值得到
-
先确定位数: ± 2 n − 1 \pm2^{n-1} ±2n−1,正数小于,负数大于。
3的表示: 3 < 2 2 = 2 3 − 1 3 < 2^2=2^{3-1} 3<22=23−1,所以用三位二进制表示。
-3的表示: − 3 > − 2 2 = − 2 3 − 1 -3>-2^{2}=-2^{3-1} −3>−22=−23−1,所以用三位二进制表示。
这个3位是恰好的位数,既体现了符号位,数字中又没有多余的0。 -
再按公式得到的十进制数→二进制数
如:3的表示: ( 3 ) D → ( 11 ) B → ( 011 ) 原 (3)_D \to (11)_B \to (011)_{原} (3)D→(11)B→(011)原,用三位二进制011表示(高位补一个零,0其实是符号位)。
-3的表示: ( 2 3 − 1 − ( − 3 ) ) D → ( 7 ) D → ( 111 ) B → ( 111 ) 原 (2^{3-1}-(-3))_D→(7)_D \to (111)_B→(111)_{原} (23−1−(−3))D→(7)D→(111)B→(111)原,用三位二进制111表示。 -
若要指定位数:在次高位(相当于是符号位后面)补0.
指定5位原码:- 正数:次高位补0。如[3]原=0跟00跟11=00011
- 负数:次高位补0。如[-3]原=1跟00跟11=10011
直接得到指定位数的原码:
- 正数还得补零:3的5位原码: ( 3 ) D → ( 11 ) B → ( 011 ) 原 → ( 00011 ) 原 (3)_D \to (11)_B \to (011)_{原}→(00011)_{原} (3)D→(11)B→(011)原→(00011)原
- 负数直接得到:-3的5位原码: [ 2 5 − 1 − ( − 3 ) ] D → ( 19 ) D → ( 10011 ) 原 [2^{5-1}-(-3)]_D \to (19)_D \to (10011)_{原} [25−1−(−3)]D→(19)D→(10011)原
表示方式2:原码=[符号位][数值位],给定位数。
符号位:0 表示正数。符号位为 1表示负数。
数值位即将真值的绝对值转换成二进制数,不够的位数次高位补0(符号位后面)。
指定5位原码:
- 正数:高位补0。如[3]原=0跟00跟11=00011
- 负数:高位补1。如[-3]原=1跟00跟11=10011
PS:纯整数和纯小数的数值位的表示方法(十进制到二进制)同数电:https://blog.csdn.net/sandalphon4869/article/details/88298591#三、数制转换
总结:指定位数
不管正负,都是在符号位后面补0
(2)小数的原码
表示方法一:按整数原码的定义
-
按公式得到的十进制数→二进制数
如:
X=0.46875的原码表示: ( 0.46875 ) D → ( 0.01111 ) B (0.46875)_D \to (0.01111)_B (0.46875)D→(0.01111)B
X=-0.46875的原码表示: ( 1 − ( − 0.46875 ) ) D = ( 1.46875 ) D → ( 1.01111 ) B (1-(-0.46875))_D=(1.46875)_D \to (1.01111)_B (1−(−0.46875))D=(1.46875)D→(1.01111)B -
若要指定位数,在末位补0
如:指定8位
若 X=0.46875 ,[X]原 =0.0111100
若 X=-0.46875,[X]原 =1.0111100
表示方式2:原码=[符号位][数值位]
符号位为 0 表示正数,为 1表示负数。
数值位即真值的绝对值(后面的补零个数=位数-符号位的位数1个-真值位的位数)。
如:
- 若 X=0.46875 ,用包括符号位为 8 位的定点原码表示,则可表示为:[X]原 =0.0111100
- 若 X=-0.46875,用包括符号位为 8 位的定点原码表示,则可表示为:[X]原 =1.0111100
指定位数:
不管正负,都是在末位补0.
(3)特性
零的问题:有两种表示形式+0和-0(符号位)
以 8 位原码表示的 0 为:
[+0]原=0.0000000 或[+0]原=00000000,
[-0]原=1.0000000 或[-0]原=10000000
可见[+0]原不等于[-0]原.
范围
原码 n 位(包括一位符号位):
- 整数数值范围分别为: − ( 2 n − 1 - 1 ) ~ + ( 2 n − 1 - 1 ) -(2^{n-1}-1)~+(2^{n-1}-1) −(2n−1-1)~+(2n−1-1)
- 纯小数所能表示的: − ( 1 − 2 − ( n − 1 ) ) ~ 1 - 2 − ( n − 1 ) {-(1-2^{-(n-1)})~1-2^{-(n-1)} } −(1−2−(n−1))~1-2−(n−1)
2.补码
(1)整数补码
确定位数: ± 2 n − 1 \pm2^{n-1} ±2n−1
正数小于,负数大于等于。
如:35的表示: 35 < 2 6 = 2 7 − 1 35 < 2^6=2^{7-1} 35<26=27−1,所以用七位二进制表示。
-35的表示: − 35 ≥ − 2 6 = − 2 7 − 1 -35 \geq -2^{6}=-2^{7-1} −35≥−26=−27−1,所以用七位二进制表示。
正整数的补码:同原码
如:真值35的原码
- 定义法: ( 35 ) D → ( 10 0011 ) B → ( 010 0011 ) 原 (35)_D \to (10\ 0011)B \to (010\ 0011)_{原} (35)D→(10 0011)B→(010 0011)原
- 格式法:0跟10 0011,所以010 0011
若指定8位,次高位补0,则[35]原=0跟0跟10 0011=0010 0011。
负整数的补码:
如:-35的补码
①8位定义法表示: 2 8 + X = 256 + ( − 35 ) = ( 221 ) D → ( 11011101 ) B 2^{8}+X=256+(-35)=(221)_D \to (1101 1101)_B 28+X=256+(−35)=(221)D→(11011101)B,1101 1101即为所求。
②对应正数的8位原码表示,包括符号位在内各位取反,(获得-35的反码),再在最低位上加 1。
③负数的8位原码表示,不包括符号位各位取反,(获得-35的反码),再在最低位上加 1。
④对应正数的8位原码表示,从最低位逐位向高位找起,找到第一个1不变,以后各位1变0、0变1,包括符号位。
若指定位数,负数次高位补1
例子:-12的8位补码
①2^8-12=244=1111 0100
②-12对应正数12的原码(0000 1100)→所有位取反(1111 0011)→+1(1111 0100)
③-12对应负数-12的原码(1000 1100)→符号位不变,其他位取反(1111 0011)→+1(1111 0100)
④-12对应正数12的原码(0000 1100)→从右往左,第一个1左边全部取反→(1111 0100)
(2)小数的补码
正小数的补码:同正小数的原码
若纯小数 X=0.46875 ,用包括符号位为 8 位的定点补码表示,则可表示为:[X]补 =0.0111100
负小数的补码:同负整数的补码方法一样
若纯小数 X=-0.46875 ,用包括符号位为 8 位的定点补码表示,则可表示为:[X]补 =1.1000100
(3)特性
求补运算【链接】
https://blog.csdn.net/sandalphon4869/article/details/90614068#2_31
简化加减法【链接】
https://blog.csdn.net/sandalphon4869/article/details/90614068#3_55
可以明显地看出大小
当同正负时,补码本身表示二进制数,越大越大,越小越小。如1111(-1)比1000(-8)大。
PS:移码则是不论同正负都是如此。
范围
通过上述说明,n 位补码表示的整数数值范围为: − 2 n − 1 到 2 n − 1 − 1 -2^{n-1} 到 2^{n-1}-1 −2n−1到2n−1−1。
n 位补码表示的小数数值范围为: − 1 到 1 - 2 − n + 1 -1到1-2^{-n+1} −1到1-2−n+1
0 的表示是唯一的
[+0]补 =0.0000000
[-0]补 =2+(-0.0000000)=10.0000000-0.0000000=0.0000000
显然[+0]补 =[-0]补=0.0000000,即补码中的“零”只有一种表示形式。
变形码(双符号位)
规则:采用两位表示符号,即 00 表示正号、11 表示负号。第一位符号位记作S2,第二位符号位记作S1。
作用:一旦发生溢出,则两个符号位就一定不一致,利用判别两个符号位是否一致便可以判定是否发生了溢出。
当模数为 4 时,形成了双符号位的补码,如 X=-0.1001,对(mod 22)而言。
[X]补= 22 +X=100.0000 000-0.1001 000=11.0111 000
算术左移、右移
| 符号 | 逻辑 | 规则 |
|---|---|---|
| << | 左移 | 各二进位全部左移指定的位数,高位丢弃,低位补0(相当于 × 2 移 的 位 数 ×2^{移的位数} ×2移的位数) |
| >> | 右移 | 各二进位全部右移指定的位数,低位丢弃,正数(次)高位补0,负数(次)高位补1(相当于 ÷ 2 移 的 位 数 \div 2^{移的位数} ÷2移的位数) |
3.反码
反码通常用来作为由原码求补码或者由补码求原码的中间过渡。
(1)整数的反码
正整数的反码:同补码,同原码
若 X=35,其 8 位反码表示为: [X]反 =0010 0011
负整数的反码:
①负数对应的正数的原码:包据符号位全部取反获得。
②负数的原码:保持符号位不变,其余各位(对数值位)取反来获得
例 5:
若 X=-35,其8位反码表示为: [X]反 =1101 1100
①~(正整数的原码)=~(0010 0011)=1101 1100
②[1][~(负整数原码的数值位)]=[1][~(010 0011)]=1101 1100
(2)小数的反码
(3)特性
两种0 的表示
在数值的反码表示中,0 同样有两种表示形式,用 8 位表示如下:
[ + 0 ] 反 = 0.000 0000 = 0000 0000 [+0]反=0.000\ 0000=0000\ 0000 [+0]反=0.000 0000=0000 0000
[ - 0 ] 反 = 1.111 1111 = 1111 1111 [-0]反=1.111\ 1111=1111\ 1111 [-0]反=1.111 1111=1111 1111
负数反码与补码的关系
从反码及补码的定义可以看到:
-
整数:
[ X ] 反 = 2 n − 1 + X [X]反 =2^{n}-1+X [X]反=2n−1+X
[ X ] 补 = 2 n + X [X]补 =2^n+X [X]补=2n+X
可见, [ X ] 补 = [ X ] 反 + 1 [X]补 =[X]反 +1 [X]补=[X]反+1 -
小数:
[ X ] 反 = 2 - 2 − n + 1 + X [X]反 =2-2^{-n+1}+X [X]反=2-2−n+1+X
[ X ] 补 = 2 + X [X]补 =2+X [X]补=2+X
可见, [ X ] 补 = [ X ] 反 + 2 − n + 1 [X]补 =[X]反 +2^{-n+1} [X]补=[X]反+2−n+1
进一步验证了前面的结论:只要在某数值的反码的最低位上加 1 即可获得该数值的补码。
数值范围
同原码:
n 位反码表示的整数数值范围为: - ( 2 n − 1 - 1 ) 到 + ( 2 n − 1 - 1 ) -(2^{n-1}-1)到+(2^{n-1}-1) -(2n−1-1)到+(2n−1-1)
n 位反码表示的小数数值范围为: - ( 1 - 2 − n − 1 ) 到 + ( 1 - 2 − ( n − 1 ) ) -(1-2^{-n-1})到+(1-2^{-(n-1)}) -(1-2−n−1)到+(1-2−(n−1))
4.移码
由于移码多用于浮点数中表示阶码,均为整数,只介绍定点整数的移码表示。
(1)整数的移码
求出该数的补码表示,而后将符号位取反。
8 位字长移码:
X=35,[X]补 =0010 0011,[X]移=1010 0011。
X=-35, [X]补 =1101 1101,[X]移=0101 1101。
定义求
8 位字长移码
X=35,[X]移=2^(n-1)+X=163=1010 0011。
X=-35,[X]移=2^(n-1)+X=93=0101 1101
(2)特性
移码的零
移码表示中,0 有唯一的编码为 1000…0
移码与补码的关系
只要将补码的符号位取反,则补码就转换成了相应的移码;同样,只要将移码的符号位取反,则移码就转换成了相应的补码。
进而可以想到,只要字长相同,补码与移码所能表示的数值范围是相同的。
移码码值的大小就反映了数值的大小
正数移码的码值一定大于负数移码的码值。也就是说,大码值所表示的数值一定大于小码值所表示的数值
5.题
- 反推(难点原码-0和补码的最小负值)

答案:-0、-128、-127、0(注意原码是-0)
先化成2进制,80H→1000 0000B。
原码1000 0000→-0
补码1000 0000→补位增(1 1000 0000)→正数的原码(0 1000 0000)→-128
反码1000 0000→正数的原码(0111 1111)→-127
移码1000 0000→补码0000 0000→0
三、浮点数
1.浮点数的表示
如:–(53/512)
-
表示方法1:
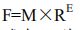
如, x = - 0.110101 × 2 − 11 x=-0.110101 \times 2^{-11} x=-0.110101×2−11.(-11是二进制数,表示-3,2的-3次方)。式中- M 为尾数(负号直接写,是二进制小数),
- E 为阶码(负号直接写,不是原码也不是补码什么的,而是二进制数),
- R 是基数(或基值)。
-
表示方法2:

①阶码和尾数通常会用特殊的形式,如补码或者移码②阶码E:用表示方法2,符号位就是阶符,数值位就是阶码。
③尾数M:用表示方法2,符号位就是数符,数值位就是尾数。
④阶码E通常为带符号的纯整数,尾数M为带符号的纯小数。
如:
浮点数字长为 16 位,其中阶码为 6 位(含一位阶符),尾数为 10 位(含一位数符),阶码用移码,尾数用补码的形式。
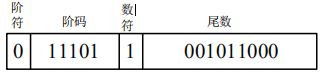
通常不画图,阶码和尾数中间留个空写出来就行: [ x ] 浮 = 011101 1.001011000 [x]浮=011101 \quad 1.001011000 [x]浮=0111011.001011000
过程在下面。
2.非规格化浮点数
范围
以通式 F=M×R^E为例,设浮点数的基值 R=2;阶码的数值位取 k 位,阶符 1 位且采用补码表示;尾数的数值位取 n 位,尾符 1 位,同样采用补码表示。
3.规格化的浮点数
(1)什么是规格化的浮点数
就是将尾数的绝对值限定在一个规定的数值范围内。当基值R为 2 时,规格化浮点数尾数的绝对值|M|应再0.5和1之间。(负数的绝对值可以取到1,正数的绝对值可以取到0.5)
尾数格式
当尾数 M 用补码表示(n是尾数的数值位的位数,不包含符号位)
- 当 M≥0 时,规格化尾数的形式必须为:
M=0.1XX…X
(即 0.5 ≤ 1 × 2 − 1 + X × 2 − 2 + . . . ≤ + ( 1 - 2 − n ) 0.5 \leq 1\times 2^{-1}+X\times 2^{-2}+...\leq+(1-2^{-n}) 0.5≤1×2−1+X×2−2+...≤+(1-2−n),所以小数点后一位必须为1)
(则尾数的最小正值为:+1/2 ,尾数的最大正值为: + ( 1 - 2 − n ) +(1-2^{-n}) +(1-2−n) 。) - 当 M<0 时,规格化尾数的形式必须为:
M=1.0XX…X
(求补可以得到它的正小数补码: 0.1 X ‾ X ‾ . . . X ‾ + 2 − n 0.1\overline{X}\overline{X}...\overline{X}+2^{-n} 0.1XX...X+2−n,即 + ( 1 / 2 + 2 − n ) ≤ 1 × 2 − 1 + X ‾ × 2 − 2 + . . . + X ‾ × 2 − n + 2 − n ≤ 1 +(1/2+2^{-n}) \leq 1\times 2^{-1}+\overline{X}\times 2^{-2}+...+\overline{X}\times 2^{-n}+2^{-n} \leq 1 +(1/2+2−n)≤1×2−1+X×2−2+...+X×2−n+2−n≤1,所以小数点后一位必须为0)
(尾数的最小负值为:-1 ,尾数的最大负值为: − ( 1 / 2 + 2 − n ) -(1/2+2^{-n}) −(1/2+2−n) 。)
(2)表示范围
规格化尾数M的数值范围
(n是尾数的数值位的位数,不包含符号位)
尾数的最小正值为:+1/2 ,尾数的最大正值为: + ( 1 - 2 − n ) +(1-2^{-n}) +(1-2−n) 。
尾数的最小负值为:-1 ,尾数的最大负值为: − ( 1 / 2 + 2 − n ) -(1/2+2^{-n}) −(1/2+2−n) 。
总的来说, − 1 到 + ( 1 - 2 − n ) -1 到+(1-2^{-n}) −1到+(1-2−n)
阶码E所表示的数值范围
与非规格化浮点数是一样的
规格化浮点数的数值范围

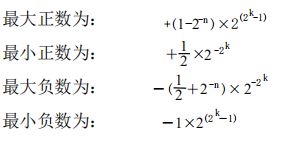
k是阶码的数值位的位数,n是尾数的数值位的位数。(都不包含符号位)
表示范围: − 1 × 2 2 k − 1 到 ( 1 − 2 − n ) × 2 2 k − 1 -1\times 2^{2^k-1}到(1-2^{-n})\times 2^{2^k-1} −1×22k−1到(1−2−n)×22k−1
例题
某浮点数格式如下:7位阶码(包含一个符号位),9位尾数(包含一个符号位),若阶码用移码、尾数用补码表示,则浮点数的表示范围是:
解析:将k=6,n=8代入最小负数和最大正数。
− 2 63 到 ( 1 − 2 − 8 ) × 2 63 -2^{63} 到 (1-2^{-8})\times 2^{63} −263到(1−2−8)×263。
(3)溢出
溢出
当浮点数阶码大于最大阶码时,称为“上溢”,此时机器停止运算,进行中断溢出处理;当浮点数阶码小于最小阶码时,称为“下溢”,此时“溢出”的数绝对值很小,通常将尾数各位强置为零,按机器零处理。
4.规格化浮点数
(1)规格化
将非规格化数转换成规格化数的过程叫做规格化。
当尾数不是规格化数时
通过修改阶码并同时左右移尾数的办法,使其变成规格化数。
对于基数不同的浮点数:左规和右规
说白了,就是移动小数点位数,指数改变, 100 = 1 × 1 0 2 = 100 × 1 0 − 1 100=1 \times 10^2=100 \times 10^{-1} 100=1×102=100×10−1
当基数R为 2 时,
左规(向左规格化):尾数左移一位,相当于 × 2 1 \times 2^1 ×21,为保持不变则阶码减 1。
右规(向右规格化):尾数右移一位,相当于 ÷ 2 1 \div 2^1 ÷21,为保持不变则阶码加 1。
(2)例题
例 6: 将十进制数 X=+13/128 写成二进制定点数和浮点数(尾数部分取 7 位,阶码部分取 7 位,阶符和数符各取 1 位,阶码采用移码,尾数用补码表示),分别写出该数的定点数和浮点数的表示形式。
解:
定点数真值表示: [X]B=0.0001 101
定点编码表示:[X]原=[X]补=[X]反=0.0001 101
规格化浮点数真值表示: X = 0.1101 000 × 2 − 11 X=0.1101\ 000×2^{-11} X=0.1101 000×2−11(左移3位,-11是二进制数即-3)
规格化浮点编码表示形式如图所示:
(阶码E-3的八位补码是1111 1101,移码是0111 1101,即阶符0,阶码111 1101)
(尾数M0.1101 000的数符是0,尾数是1101 000)

例 7: 设浮点数字长为 16 位,其中阶码为 6 位(含一位阶符),尾数为 10 位(含一位数符),写出 X= –(53/512)对应的浮点规格化数阶码用移码,尾数用补码的形式。
解: X = – ( 53 / 512 ) = - 0.0001 1010 1 = ( - 0.1101 0100 0 ) × 2 − 11 X= –(53/512)= -0.0001\ 1010\ 1= (-0.1101\ 0100\ 0)\times 2^{-11} X=–(53/512)=-0.0001 1010 1=(-0.1101 0100 0)×2−11
尾数的规格化补码形式为:1.0010 1100 0
(方法是负数的补码方法4,用负数对应正数的原码从右往左,第一个1左边全部取反,所以负号就直接写着)
阶码的移码表示为:-3→3原码:00 0011→-3补码:11 1101→-3移码:01 1101
浮点表示形式如图所示:

四、其他的数据表示
1.IEEE754
参数:
- ( − 1 ) S (-1)^S (−1)S:该浮点数的数符,当s为0时表示为正数,s为1时为负数
- E:指数,用移码表示
- ( b 0 。 b 1 b 2 b 3 . . . b p - 1 ) (b_0。b_1b_2b_3...b_{p-1}) (b0。b1b2b3...bp-1):尾数,共P位,用原码表示。
(1)单精度格式(32位)

s为数符为1位,阶码为8位(含1位阶符),f为尾数为23位。
- 规格化时b0必须为1而且应隐去。
- 阶码加01111111
例8:现欲利用IEEE754标准将数176.0625表示为单精度浮点数。
①转化成正数:
本来是正数自然没有影响,s=0,如果是负数,则之后讨论的都是它的正数,并且s=1。
②将该十进制来转换成二进制数:
( 176.0625 ) 10 = ( 10110000.0001 ) 2 (176.0625)_{10}=(1011 0000.0001)_2 (176.0625)10=(10110000.0001)2
③对上面二进制数规格化:
10110000.0001=1◆0110 0000 001×2^7
这就保证了使b0为1,而且小数点在◆位置上。将b0去掉并扩展为单精度浮点数所规定的23位尾数:0110 0000 0010 0000 0000 000。
④现在, 再来求取阶码。
阶数的真值+真值127,然后将结果转化为二进制(第一位不表示符号位)
现指数为7即真值,而单精度浮点数规定指数的偏移量为127(请注意不是前面移码描述中所提到的128),即在指数7上加127,也就是e=7+127=134,从而得到则指数的移码表示为1000 0110。
⑤最后,将 ( 176.0625 ) 10 (176.0625)_{10} (176.0625)10表示为IEEE–754标准的单精度浮点数:
0 10000110 01100000001000000000000
(2)双精度格式(64位)

[ S : 1 个 ] [ E : 11 个 ] [ F : 52 个 ] [S:1个][E:11个][F:52个] [S:1个][E:11个][F:52个]
2.奇偶校验码
(1)水平奇偶校验
水平奇校验
设数据 X = ( x 0 x 1 ⋅ ⋅ ⋅ x n − 1 ) X=(x_0x_1···x_{n-1}) X=(x0x1⋅⋅⋅xn−1)是一个 n 位字,若在其高位前增加 1 位奇校验位 c,
保证![]()
即,![]()
例如:
X=01010100,采用奇校验时,奇校验位 c 必须为 0,则加了奇校验的数据 X′=001010100。
X=01010101,采用奇校验时,奇校验位 c 必须为 1,则加了奇校验的数据 X′=101010101。
水平偶校验
设数据 X = ( x 0 x 1 ⋅ ⋅ ⋅ x n − 1 ) X=(x_0x_1···x_{n-1}) X=(x0x1⋅⋅⋅xn−1)是一个 n 位字,若在其高位前增加 1 位奇校验位 c,
保证![]()
即,![]()
例如:
X=01010100,采用偶校验时,偶校验位 c 必须为 1,则加了奇校验的数据 X′=101010100。
X=01010101,采用偶校验时,偶校验位 c 必须为 0,则加了奇校验的数据 X′=001010101。
(2)垂直奇偶校验码
(2)水平垂直奇偶校验码
3.海明码
https://blog.csdn.net/CeleCoCo/article/details/83507640
4.循环冗余校验码(CRC 码)
(1)模运算
- 模 2 加法 按位加,不考虑进位:0+0=0,0+1=1,1+0=1,1+1=0.例如 1101+1011=0110。
- 模 2 减法 按位减,不考虑借位:0-0=0,0-1=1,1-0=1,1-1=0.例如 1101-1011=0110。
可见模 2 减法与模 2 加法运算结果相同,因此可用模 2 加法代替模 2 减法。 - 模 2 乘法 按模 2 加求部分积之和,不考虑进位。例如 1010×1101=1110010。
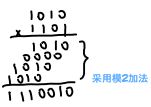
- 模 2 除法 按模 2 减求部分余数,不借位,每求一位商应使部分余数减少一位。
进商的规则是:余数首位为 1 商取 1,余数首位为 0 商取 0。当余数位数小于除数位数时即为最后余数。例如 10000÷101=101+01/101,商为 101,余数为 01。
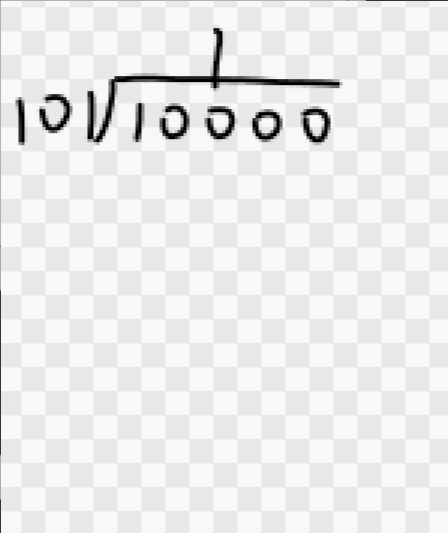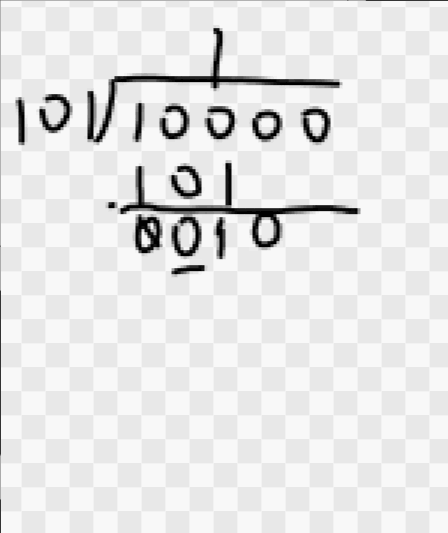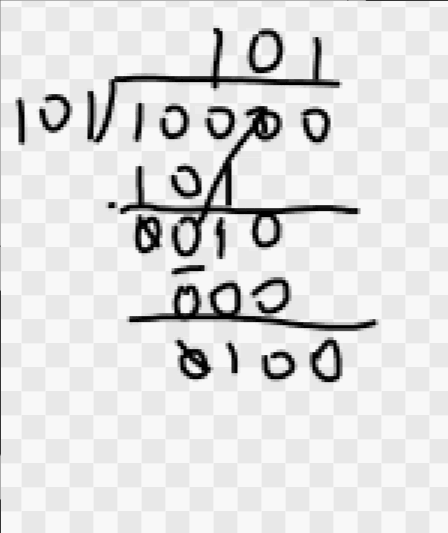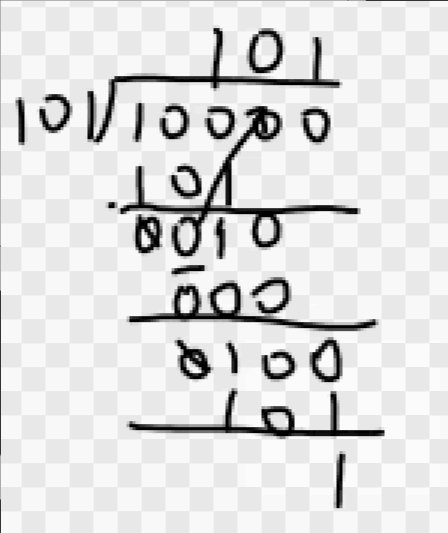
上述这些法则,在后面求 CRC 校验码时将会用到。
(2)CRC 码的编码
步骤:
-
将有效信息 M(X) 化作数字表示:
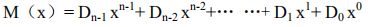
如: M ( X ) = x 3 + x 2 = 1100 M(X)=x^3+x^2=1100 M(X)=x3+x2=1100 -
求余数的位数k:
k = 生 成 多 项 式 G ( X ) 的 位 数 − 1 k=生成多项式G(X)的位数-1 k=生成多项式G(X)的位数−1
如:G(x)=1011,则k=4-1=3 -
将有效信息 M(X) 左移k位,低位补0
如:1100左移3位,1100000 -
将左移后的有效信息被 G(X) 模2除,得到余数
如:1100000与1011模2除,得到余数010 -
将左移后的有效信息和余数拼接
如:1100000+010=1100010
(2)CRC 码的译码校验
将得到的CRC码除以生成多项式,如果余数是000,正确;否则,错误。