广义线性模型GLM

本文转自 GLM(广义线性模型) 与 LR(逻辑回归) 详解（原作者：爱学习的段哥哥）

GLM的内容，本应该较早之前就总结的，但一直觉得这种教科书上的基础知识不值得专门花时间copy到博客里来。直到某一天看到一篇不错的总结，在征求作者同意后，转载于此（本人比较懒啦）（然而公式重新排版竟然花了1个多小时TT）。

原文如下

George Box said: “All models are wrong, some are useful”

1. 始于 Linear Model

作为 GLM 的基础，本节 review 经典的 Linear Regression，并阐述一些基础 term。 
我们线性回归的基本如下述公式，本质上是想通过观察，然后以一个简单的线性函数 来预测 :
      

1.1 dependent variable

这是我们的预测目标，也称 response variable。这里有一个容易混淆的点，实际上 可以表达三种含义（建模用的是分布，观察到的是采样，预测的是期望）：

distribution；抽象地讨论 response variable 时，我们实际上关注对于给定数据和参数时， 服从的分布。Linear Regression 的 服从高斯分布，具体取值是实数，但这里我们关注的是分布。
observed outcome；我们的 label，有时用 区分表示；这是真正观察到的结果，只是一个值。
expected outcome； 表示模型的预测；注意 实际上服从一个分布，但预测结果是整个分布的均值 ，只是一个值。

1.2 independent variable

这是我们的特征，可以包含很多维度，一个特征也称为一个 predictor。

1.3 hypothesis
线性模型的假设非常简单，即 inner product of weight vector and feature vector，被称为 linear predictor。这是就是线性模型，GLM 也是基与此的推广。 
深入来看，各个维度特征（predictor）  通过系数  线性加和，这一过程将信息进行了整合；而不同的 weight（coefficient） 反映了相关特征不同的贡献程度 。

2. 推广到 Generalized Linear Model

2.1 Motive & Definition

线性模型有着非常强的局限，即 response variable 必须服从高斯分布；主要的局限是拟合目标 的 scale 是一个实数 。具体来说有俩个问题：

的取值范围和一些常见问题不匹配。例如 count（游客人数统计恒为正）以及 binary（某个二分类问题）
的方差是常数 constant。有些问题上方差可能依赖 的均值，例如我预测目标值越大方也越大（预测越不精确）
所以这时我们使用 Generalized Linear Model 来克服这俩个问题。 
一句话定义 GLM 即（from wiki）： 
In statistics, the generalized linear model (GLM) is a flexible generalization of ordinary linear regression that allows for response variables that have error distribution models other than a normal distribution. 
详细来说，我们可以把 GLM 分解为 Random Component、System Component 和 Link Function 三个部分。

2.2 Random Component

An exponential family model for the response

这里是指 response variable 必须服从某一 exponential family distribution 指数族分布，即 ， 指 exponential family 的 natural parameter 自然参数。 
例如 linear regression 服从 Gaussian 高斯分布，logistic regression 服从 Bernoulli 伯努利分布。指数族还有很多分布如 多项分布、拉普拉斯分布、泊松分布等等。 
另外，这也可以被称为 Error Structure : error distribution model for the response。对于 Gaussian 的 residual 残差 服从高斯分布  是很直观可；但是，例如 Bernoulli 则没有直接的 error term。可以构造其他的 residual 服从 Binomial，但是较抽象，本文不对此角度展开。

2.3 Systematic Component

linear predictor

广义线性模型 GLM 本质上还是线性模型，我们推广的只是 response variable yy 的分布，模型最终学习的目标还是 linear predictor 中的 weight vector。 
注意，GLM 的一个较强的假设是，即 yy 相关的 exponential family 的 natural parameter 等于 linear predictor。这个假设倾向于是一种 design choice（from Andrew），不过这种 choice 是有合理性的，至少 和 linear predictor 的 scale 是一致的。

2.4 Link Function

A link function connects the mean of the response to the linear predictor

通过上述的 Random Component 和 Systematic Component，我们已经把 和 统一到了 exponential family distribution 中，最终的一步就是通过 link function 建立俩者联系。对任意 exponential family distribution，都存在 link function ， 是 分布的均值 而 是 natural parameter；例如 Gaussian 的 link function 是 identity（），Bernoulli 的 link function 是 logit，即： 。 
link function 建立了response variable 分布均值（实际就是我们的预测目标） 和 linear predictor 的关系（准确来说，这只在 条件下成立，但大多数情况都条件都成立，这里不展开说明）。实际上 link function 把原始 的 scale 转换统一到了 linear predictor 的 scale 上。另外，不同分布的 link function 可以通过原始分布公式变换到指数组分布形式来直接推出，之后本文第4章会有详细讲解。 
最后要强调的是，link function 的反函数 称为 响应函数 response function。响应函数 把 linear predictor 直接映射到了预测目标 ，较常用的响应函数例如 logistic/sigmoid、softmax（都是 logit 的反函数）。

2.5 Contrast between LM & GLM

• linear predictor

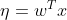
Linear Regression

• response variable
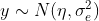
• link function 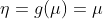, called identity
• prediction

Generalized Linear Model

• response variable
• link function 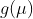, eg. logit for Bernoulli
• prediction , eg.logistic for Bernoulli

这里再次强调了他们 linear predictor 的部分是一致的；不过对 response variable 服从分布的假设不一致。Gaussian 的 response function 是 ；而 exponential family 根据具体假设的分布，使用相应的 response function （例如 Bernoulli 是 sigmoid）。

额外强调一个点，无论是 LM 还是 GLM，我们对不同数据 得到的其实是不同的 response variable 的分布，所以不同分布的 值不同，进而我们预测的结果不同。虽然每一条数据只是预测了一个值，但其实对应的是一个分布。并且数据相似的话对应的分布也相似，那么预测结果也相似。

3. 实例：Linear Regression 到 Logistic Regression

GLM 中我们最常用到的是 Logistic Regression；即假设 服从 Bernoulli 伯努利分布，这里详细展开阐述。

3.1 以 GLM 来看 Logistic Regression

以下直接列出相关的 GLM 概念对 LR 的解释：

• An exponential family (random component)
• linearl predictor (system component)：，这个部分 GLM 都有且都一致
• link function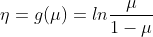：，这个函数是 log-odds，又称 logit 函数
• response function：，称为 logistic 或 sigmoid
• prediction：
• loss function : 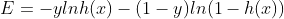, 和 Linear Model 一样由 MLE 推导得到，3.3 中会给出详细推导过程

Scale Insight 可以给我们更多 link function 的理解：

• binary outcome：0 or 1，对应 observed outcome 即 label
• probability：[0,1]，对应 expected outcome，即 的分布的
• odds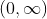：，概率和几率可相互转换  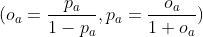；即是发生概率与不发生概率的比，赌博中常见这一概念，和赔率相关
• log-odds/logit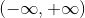：，即

所以 log-odds 在 scale 上和 linear predictor 匹配。对于 Logistic Regression，我们通过 link function logit 建立了与简单线性模型的关联。link function 就是把任意 exponential family distribution 的均值 映射到线性尺度上： 

      

      

即是，在 Logistic Regression 模型中，输出 的 log-odds 对数几率是关于输入 的线性函数。

3.2 Logistic/Sigmoid 函数

此函数是 Bernoulli 在 GLM 的 response function，即 link function 的反函数。（强调反函数的时候可以使用 标识；当然直接使用 也没问题，Andrew 课上使用的是后者） 
此函数在神经网络中也有用作 activate function 来引入非线性（当然现在更常用 rectified linear unit, ReLU），其拥有一些特点：

• bounded 有界的，取值 (0,1)，有概率意义
• monotonic 单调递增函数
• differentiable 可微，且求导简单

函数呈 S 曲线，中央区域敏感，两侧抑制（有俩个优点：首先是符合神经激活原理；其次是现实问题会有类似的非线性关系，当自变量很大或很小时对因变量影响很小，但是在某个阈值范围上时影响很大）
这里展开证明一下求导简单，即 ： 
      
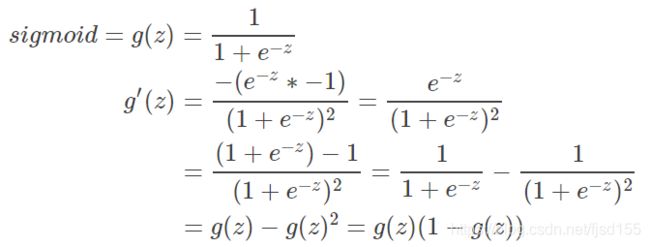
另外，这里先证明一个有趣的特性 （为后续章节证明流程铺垫~） 
      
logistic/sigmoid 函数还有一些其他的解释，例如生态学模型。

3.3 LR 的 loss function

3.3.1 标准套路

本节详细完成 logistic regression 剩下部分的阐述。假设我们观察到了数据集 包含 个样本， 表示某一样本的特征向量，=0 or 1 表示这一样本的真实类别（observed outcome）。另外定义 为模型的输出结果（expected outcome）。我们假设 服从 Bernoulli 伯努利分布（），则可以写出似然函数如下： 
      

对似然函数取对数化简如下： 
      

所以 loss fucntion 可以写为（最大化似然 转 最小化cost）： 
      
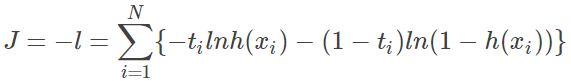
这是基于 binomial 二项分布推导出来的 loss，所以又被称为 negative binomial log-likelihood。
其中 依照 GLM 理论，依据 response function 展开为：

为 loss function 带入 对 weight vector 求导（注意 Chain Rule）： 
      

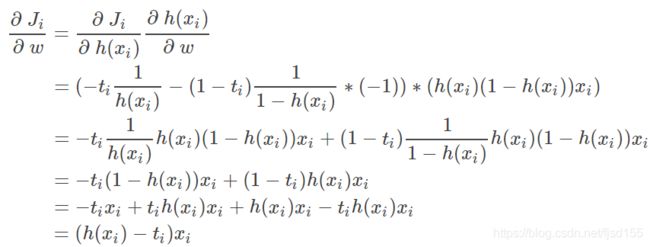
所以 Logistic Regression 与 Linear Regression 更新公式（Batch Gradient Descent）是类似的，唯一不同点在于不同的 response function ： 
      

3.3.2 其他套路

这里专门强调一下，有一些论文里面会使用其他形式的等价的 negative binomial log-likelihood： 
      

这个形式要简洁很多，但实际和上小节中 loss function  完全等价的，唯一的区别是：这里使用的 label 而非上一小节的 。这种表达有一个好处， 是 linear predictor，上小节有 ，但是这里更 general，可以用其他方式定义来定义这个 linear predictor，例如 GBDT 中的函数加和，其实这个 loss 就是从 GBDT 论文上看到的~以下将证明这一套路与标准讨论等价：
首先，把原 loss 展开 （把 inverse 符号去掉了，这里不需要再强调了），且根据 sigmoid 的 ，有： 
      

对 label 分情况展开： 
      

切换到 （这是唯一的不同哦）： 
      

显然可以对原 loss 整合并展开为： 
      
证毕。
loss 的 gradient 当然也是完全等价的，这里简单展开部分结果： 
      

4. Exponential Family

这里补充一下 exponential family 的定义，并且给出 Bernoulli 以及 Categorical 对应的 link function 和 response function。

4.1 Definition

The exponential family of distribution over given is （ 都是确定的函数，基于 或 确定的，所以这是只以 为参数的分布）: 
      

• natural parameter 自然参数，这是决定分布的具体参数
•  sufficient statistics 充分统计量，通常有
•  是分布正规化系数 coefficient，即确保概率和为1，满足

常见的 exponential family 有 Bernoulli Distribution, Binomial Poisson Distribution, Negative Binomial Distribution, Categorical Distribution, Multinomial Distribution, Beta Distribution, Dirichlet Distribution, Laplace Distribution, Gamma Distribution, Normal Distribution 等等，所以说 GLM 极大地拓展了 LM 的使用范围。

4.2 Bernoulli Distribution

伯努利分布 的 分布律（相对于 continuous variable 的 概率密度函数） 如下：

    

我们将其变换到标准 exponential family 形式： 
      

得到 natural parameter，也正是 GLM 使用的 link function，logit：

这里推导一下其 inverse function，即 GLM 使用的 response function： 
      

这也就是 logistic/sigmoid 函数。剩余其他部分： 
      

4.3 Categorical Distribution

作为 Bernoulli 的推广，Categorical 的 link function 和 response function 与前者非常相似。其 response function 是 softmax，所以 logistic/sigmoid 和 softmax 也是一个推广关系。

这里注意一点，Categorical Distribution 即是单次的 Multiple Distribution，后者更常见。（而 Bernoulli Distribution 是单次的 Binomial Distribution）

以下介绍推导过程，分类分布的 分布律，以及 exponential family 形式如下： 
      

上述表达缺少了一个约束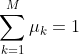：， 通常会改写分布形式来消除这个约束，即我们只确认 M−1 个 ，剩下 1 个 是一个确定的值。当然，我们其实还会有隐含的约束 和 ，这个 Bernoulli 也有。 
下面是包含约束的改写过程： 
      
所以 natural parameter 正是： 
      

这里的 是一个向量，比 Bernoulli 要复杂，因为需要考虑 M 个不同分类。上述公式中的分母其实就是 M−1 以外的那一个分类的概率 ，所以其实也有点 odds 的意思；这里可以理解为我们随意选择了一个分类作为base，然后用其他分类出现的概率对其求对数比例，把可能性的取值范围扩展到了 。作为被选择作base的分类，其 。
下面推导其 inverse function 即 GLM 使用的 response function，这个过程比 logistic 要复杂很多。首先等价变换 link function： 
      

接下来，对上式 left side 累加 M 个分类的值： 
      

对 right side 累加 M 个分类的值： 
      
俩个式子结合则有： 
      

重新代入 link function 则有： 
      

这里对于特殊的，

       

所以对任意分类上式都是成立的。 
最终，softmax 的形式为： 
      

也可以等价地写作： 
      

这个结果近似于 logistic/sigmoid 的： 
      

且 logistic/sigmoid 中第二种可能的概率为： 
      

可见 logistic/sigmoid 只是 softmax 在 M=2 时的特殊形式。