算法--递归

 目录

         一、递归算法基本概念

1.什么是递归?

2.递归栈

3.递归算法分析

 二、递归三步曲

 三、例题解析

1.斐波那契数列   斐波拉契数列

2.反转链表:  反转链表

3.链表求和  链表求和

        总结

---

前言

        本文是笔者第一次写类似的文章，旨在分享自己学习时的感悟，并用做学习的笔记。篇幅较长，但相信能给读者带来收获,如有不足欢迎指点。

---

一、递归算法基本概念

1.什么是递归?

         自己调用自己的算法称为递归算法，这就好比套娃，大的套娃里面还有一个与它相似的套娃，如此反复直到套娃大小达到足够小。

和套娃类似的递归算法，有两个基本条件:

  1.结束条件(套娃达到足够小后就没有在下一个套娃了)

  2.状态转换方程:调用本身(除最小套娃外，每个套娃下都有比他小一级的套娃)

                              (图片来源与百度） 

2.递归栈

        递归的实现是基于栈的数据结构,有先进后出的特点

3.递归算法分析

        对于递归算法的分析通常将递归算法构成递归树，进一步分析，由于本文主要讲解递归代码的编写，这里不展开讲解，感兴趣的读者可以自行查阅相关材料。

    
二、递归三步曲

        绝大多数人在写递归算法时，会比较茫然无从下手，相信按下面的步骤会对编写递归算法有较大的帮助。

     1.明确函数意义:即你写的这个函数目的是什么，有什么作用，返回值是什么。

         这个难度不大，不因为大部分时候我们都是明确了函数的作用再来编写函数的。但这并不意味着，它不重要，相反准确无误的函数意义对后续代码编写能起到大的帮助。

    2.结束条件:即何时停止递归，若结束条件填写不当，容易出现无限递归的情况。结束条件的选择，需要根据实际情况来选择。

    3.递归方程:即函数如何调用本身,先用数学语言(或自己的语言)表示出来。这是递归函数的关键。

        此外为了代码的健壮性还需考虑输入错误的情况。

        当然光说上面的步骤太抽象，下面通过上述步骤来分析几道例题，先试着自己解题在看解析效果会更好哦!

三、例题解析

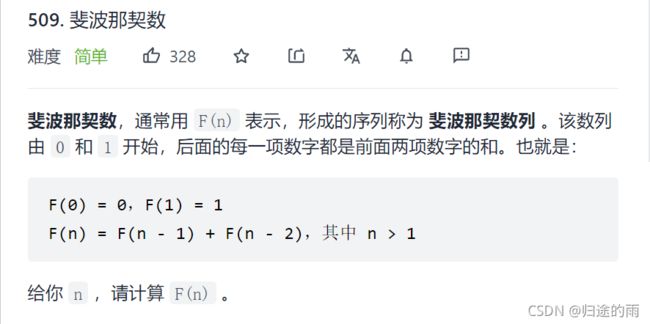
    1.斐波那契数列   斐波拉契数列

 示例:

输入：2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

输入：3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

输入：4
输出：3
解释：F(4) = F(3) + F(2) =2 + 1 = 3 

         本题的最优解并不是递归方法,但由于本问简介的是递归算法，为此下面通过递归算法来解决该题:

/*
   本题的三个步骤，题设都有明确给出:
       1.函数意义:求解F(n)   int n>=0  错误输入 n<0
       2.结束条件:
           n=0 || n=1
       3.递归方程:
           F(n)=n; n=0 || n=1
           F(n)=F(n-1)+F(n-2);n>1
*/ 

    

下面给出java代码:

class Solution {
    //递归写法
    public int fib(int n) {
        /*
            1.函数意义:求解F(n)
            2.结束条件:
                n=0 || n=1
            3.递归方程:
                fib(n)=n; n=0 || n=1
                fib(n)=fib(n-1)+fib(n-2);n>1
        */
        if(n<0) return -1; //输入不符合条件
        if(n==0 || n==1) return n;
        return fib(n-1)+fib(n-2);
    }
}

       本题题设给出了函数的数学表达式，较为简单，但大部分题目不会明显的给出式子，需要自己挖掘。

2.反转链表:  反转链表

  

         同样的本题的最优解法也不是递归，但仍然只讲解递归的方法

/*

单链表本身就具有很强的递归性

思路:

  对于一个较长的单链表,如 1->2->3->4->5

  我们可以记2->3->4->5 为链表l        

  则 原链表为: 1->l,

 那么反转链表应该分为下面三步:

(1)反转 l 得到 l' 且反转后的头节点记为newhead，显然尾节点为2(head.next);

    newhead=reverseList(head.next); 

(2) l'连接上 1    即 2->1    

      head.next.next=head;   //head.next=2   2.next=head

(3)断开  1与原链表的连线  1->2 

        head.next=null;

思考: 上述(1)(2)(3)的顺序能否互换,答案是不能。

原因:   

    步骤(1)中的l是原链表中第二个节点以及后续的节点，那么首先 2必须连着3,即2->3 不能断，若执行了步骤(2) 2->1 因为单链表的节点都比较专一，不会同时连着两个节点，显然2->3就断开了，所以必须是先(1)在(2)

    至于(2)(3)的顺序若不采用而外指针做记录，那么显然

            head.next.next=head;

             head.next=null;

    的顺序是定死的所以给先(2)在(3)

 综上顺序不能互换

1.函数意义:

        根据题意,本题的目的是反转链表,函数的输入参数的链表的头元素，返回参数是反转后的头元素

2.结束条件:

        思路中的伪代码存在head.next,为此head不能为null,而对于单节点的链表，其显然是不用反转的

        (1)head==null   return head;

        (2)head.next==null:单节点不用反转   return head;

3.递归函数:

        reverseList(head)=head;  head==null || head.next==null;

        reverseList(head)={

             newhead=reverseList(head.next); 

             head.next.next=head;

              head.next=null;

              return newhead;

        }
        

*/            

 下面给出java代码

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null || head.next==null) return head;
        ListNode newhead=reverseList(head.next); //反转头结点的下一个节点开始到尾节点的链表
        head.next.next=head;  //反转后的新链表连接头节点
        head.next=null;  //断开原有的连接
        return newhead;
    }
}

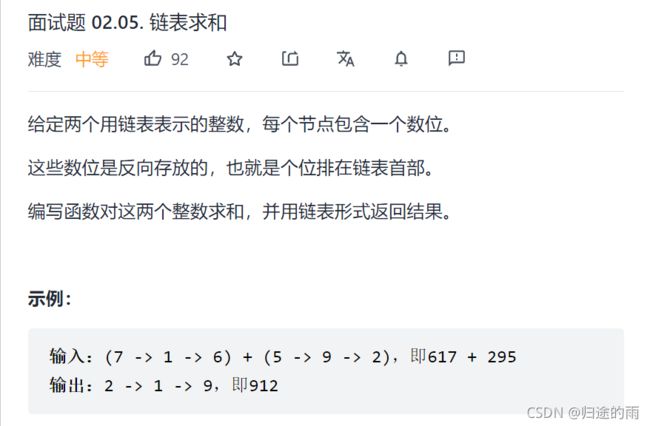
3.链表求和  链表求和

 思路:
        先来看下我们正常计算时的方法:

                              

                        

可以看出其实是反复的进行 c1+c2+cn 且逢10进1  的操作,其中c1，c2表示两个数的同位数的相同位置的单位数，cn表示低位的进位数，起始cn=0

所以大体解题思路如下:

   (1)两个头结点之和与cn相加，记作val  val=l1.val+l2.val+cn;

   (2)取val%10作为头节点head的值  head.val=val%10;

   (3)取val/10作为新的进位符，对后续节点求和，求和结果作为head的后续链表;

        head.next=addTwoNums(l1.next,l2.next,val/10);

1.函数意义:
      进位为cn的情况下对l1,l2做求和操作

      参数: ListNode l1, ListNode l2, int cn

      返回值:求和后的头结点 

 2.结束条件:

    (1)   l1==null && l2==null

          cn=0  return null;

          cn!=0 return new ListNode(cn);

        细心的读者可能有看出我上面给的例子和题设的例子不同，主要是想表达l1与l2长度可能不同，所以可能会有一个已经为null，而另外一个不是null的情况

   (2)两个有且只有一个为null

        cn=0:return 不为空的链表

        cn!=0:还需要对不为null的链表做与cn相加的操作，这里记这个操作为addcn，后面还会给出这个函数的具体实现，读者可以先将这个函数当成已经封装好的了，其功能为实现链表与某个数相加。

 3.递归函数:

     addTwoNums(l1,l2,cn) = (cn==0?l1:new ListNode(cn));  l1==null && l2==null

     addTwoNums(l1,l2,cn) ={

           ListNode head=l1==null?l2:l1;  //取不为空的链表

           return cn==0?head:addcn(head,cn);  //cn为0就直接返回非空链表，否则还要求和

     }

     addTwoNums(l1,l2,cn) ={

           int val=l1.val+l2.val+cn;  //两个头结点之和与cn相加

           ListNode head=new ListNode(val%10); //取val%10作为头节点head的值

                

          //取val/10作为新的进位符，对后续节点求和，求和结果作为head的后续链表

           head.next=addTwoNums(l1.next,l2.next,val/10); 

            return head;

   }

 下面给出java代码:
 

public ListNode addTwoNums(ListNode l1,ListNode l2,int cn){
    if(l1==null && l2==null){
        return cn==0?l1:new ListNode(cn);
    }
    if(l1==null || l2==null){
        ListNode head=l1==null?l2:l1;
        return cn==0?head:addcn(head,cn);
    }
    int val=l1.val+l2.val+cn;  //两个头结点之和与cn相加
    ListNode head=new ListNode(val%10); //取val%10作为头节点head的值
    head.next=addTwoNums(l1.next,l2.next,val/10); //取val/10作为新的进位符，对后续节点求和，求和结果作为head的后续链表
    return head;
}

上面的代码中涉及到另外一个函数，即addcn()：将链表加上某一个数

该函数可以通过递归，也可以通过迭代实现，下面讲解递归实现:
思路:

还是先上图:

      

 可以看出其实就是反复进行 c+cn 且逢10进1 ，当进位为0时停止操作

所以大体思路如下:

     1.头节点与cn相加 结果记作 val   

          val=head.val+cn

      2.取val%10作为新头节点的值 

           newhead.val=val%10;

       3.取val/10作为新进位数，与head.next及其后续节点相加,结果为newhead.next

           newhead.next=addcn(head.next,val/10);

1.函数意义: 链表代表的数+cn

2.结束条件:

    (1)cn==0 && head!=null:return head;

    (2)cn==0 && head==null:return head;

合并(1)(2)--> 

    (1)cn==0:return head;

    (2)cn!=0 && head==null:return new ListNode(cn);

3.递归方程:

     addcn(head,cn)=head; cn==0

     addcn(head,cn)=return new ListNode(cn); cn!=0 && head==null

     addcn(head.cn)={

          val=head.val+cn;

          newhead.val=val%10;

          cn=val/10;

           newhead.next=addcn(head.next,cn)

    }

public ListNode addcn(ListNode head,int cn){
    if(cn==0) return head;
    if(head==null) return new ListNode(cn); 
    int val=head.val+cn; 
    ListNode newhead=new ListNode(val%10); 
    newhead.next=addcn(head.next,val/10);
    return newhead;
}

综上本题总代码如下:
      

class Solution {
    //递归

    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        return addTwoNums(l1,l2,0);
    }

    public ListNode addTwoNums(ListNode l1,ListNode l2,int cn){
        if(l1==null && l2==null){
            return cn==0?l1:new ListNode(cn);
        }
        if(l1==null || l2==null){
            ListNode head=l1==null?l2:l1;
            return cn==0?head:addcn(head,cn);
        }
        int val=l1.val+l2.val+cn;  //两个头结点之和与cn相加
        ListNode head=new ListNode(val%10); //取val%10作为头节点head的值
        head.next=addTwoNums(l1.next,l2.next,val/10); //取val/10作为新的进位符，对后续节点求和，求和结果作为head的后续链表
        return head;
    }
    public ListNode addcn(ListNode head,int cn){
        if(cn==0) return head;
        if(head==null) return new ListNode(cn); 
        int val=head.val+cn; 
        ListNode newhead=new ListNode(val%10); 
        newhead.next=addcn(head.next,val/10);
        return newhead;
    }
}

其实对一个链表为空，另外一个链表不为空的情况，也可以把为空的链表看出n个0组成的链表（n为非空链表的长度)

由于篇幅原因这里不做讲解，只给出代码：

class Solution {
    //法二:递归
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        return addTwoNum(l1,l2,0);
    }
    public ListNode addTwoNum(ListNode l1,ListNode l2,int cn){
        if(l1==null && l2==null && cn==0) return null;

        int v=(l1!=null?l1.val:0)+(l2!=null?l2.val:0)+cn;
        int val=v%10;
        int c=v/10;
        ListNode head=new ListNode(val);
        head.next=addTwoNum(l1!=null?l1.next:null,l2!=null?l2.next:null,c);
        return head;
    }
}

除了上述讲解的问题外，还有很多递归算法的题目，读者可以自行上查找练习，下面给出几个推荐的题目:

        1.汉诺塔问题         2.最长同值路径     3.合并两个排序的链表

  下期预告(说不定是年更嘿嘿):

        算法--递归应用：笔者认为分治，深度优先搜索，回溯算法是递归的应用为此放在递归应用中进行讲解

---

总结

        本片给出了递归的概念、递归的三部曲并通过详解三个例子来具体讲解递归三部曲。

---