Logistic回归推导（三）--牛顿法及纯python实现

1、牛顿法图解

牛顿法一般用来求解方程的根或求解极值，其基本思想是：在现有极值点估计值附近对f(x)做二阶泰勒展开，从而找到极值点的下一个估计值。
下面用一个例图说明：

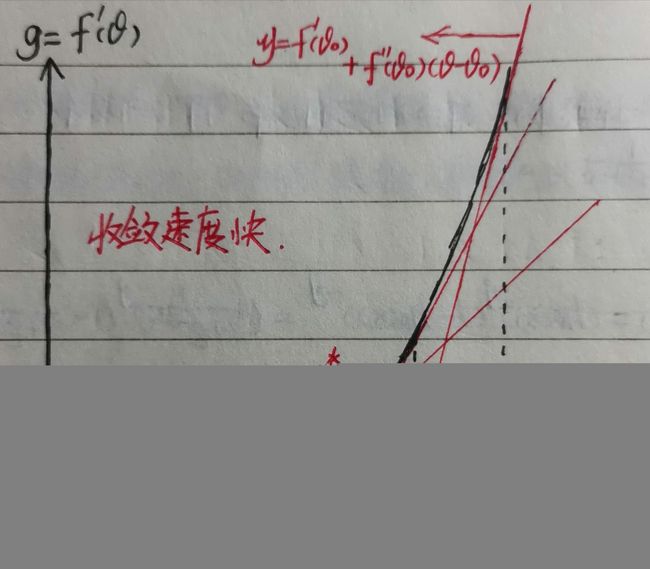
如图横坐标为参数$\theta$，纵坐标为函数一阶导数$f^{{}^{\prime }}(\theta )$，则牛顿法迭代过程如下：
(1)过点$({\theta }_0,f^{{}^{\prime }}({\theta }_0))$作切线，切线方程为$y=f^{{}^{\prime }}({\theta }_0)+f^{{}^{\prime \prime }}({\theta }_0)(\theta -{\theta }_0)$;
(2)切线交横轴于${\theta }_1={\theta }_0-\frac{f^{{}^{\prime }}({\theta }_0)}{f^{{}^{\prime \prime }}({\theta }_0)}$处;
(3)过点$({\theta }_1,f^{{}^{\prime }}({\theta }_1))$作切线，切线方程为$y=f^{{}^{\prime }}({\theta }_1)+f^{{}^{\prime \prime }}({\theta }_1)(\theta -{\theta }_1)$;
(4)切线交横轴于${\theta }_2={\theta }_1-\frac{f^{{}^{\prime }}({\theta }_1)}{f^{{}^{\prime \prime }}({\theta }_1)}$处;
(5)重复迭代得到${\theta }^{\ast }$。

2、牛顿法原理

(1)当样本只有一个特征

假设$f(x)$二次可微，设$x=x_{min}$时，函数f(x)取得最小值，我们的目标就是希望能求得$x_{min}$。
首先用$x_k$作为$x_{min}$的估计值，在$x=x_k$处进行二阶泰勒展开：
$$f(x)\approx f(x_k)+f^{{}^{\prime }}(x_k)(x-x_k)+\frac{1}{2}{f}^{{}^{\prime \prime }}(x_k)(x-x_k{)}^2$$
求$f(x)$的极值即求导数为0处的$x$，对$f(x)$求导：
$$\begin{array}{rl}{f}^{{}^{\prime }}(x)& =0+f^{{}^{\prime }}(x_k)(1-0)+\frac{1}{2}{f}^{{}^{\prime \prime }}(x_k)2(x-x_k)\\ & =f^{{}^{\prime }}(x_k)+f^{{}^{\prime \prime }}(x_k)(x-x_k)\end{array}$$
令其为0得到下一个估计值$x=x_k-\frac{f^{{}^{\prime }}(x_k)}{f^{{}^{\prime \prime }}(x_k)}$
故迭代公式为：
$$x_{k+1}=x_k-\frac{f^{{}^{\prime }}(x_k)}{f^{{}^{\prime \prime }}(x_k)}$$

(1)当样本有多个特征

二阶泰勒展开式的推广为：
$$\phi (X)\approx f(X_k)+▽f(X_k)\cdot (X-X_k)+\frac{1}{2}(X-X_k{)}^T\cdot {▽}^{2}f(X_k)\cdot (X-X_k)$$
其中$▽f$为$f$的梯度向量
$$▽f=[\frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_2}...\frac{\partial f}{\partial x_N}{]}^T$$
${▽}^{2}f$为$f$的海森矩阵。
由$▽\phi (X)=0$，即
$$▽f(X_k)+{▽}^{2}f(X_k)\cdot (X-X_k)=0$$
得下一个极值的估计值为
$$X=X_k-{▽}^{2}f(X_k{)}^{-1}▽f(X_k)$$
令$▽f=g_k，{▽}^{2}f=H_k$，则迭代公式为
$$X_{k+1}=X_k-H_k^{-1}{g}_k$$

3、牛顿法求解Logistic回归

Logistic回归假设函数为：
$$\begin{array}{rl}P(y|x;\theta )& =[h_{\theta }(x){]}^y[1-h_{\theta }(x){]}^{(1-y)}\\ & =(\frac{1}{1+e^{-{\theta }^{T}x}}{)}^y(1-\frac{1}{1+e^{-{\theta }^{T}x}}{)}^{1-y}\end{array}$$
其目标函数为：
$$\text{arg }\underset{\theta }{\max }\frac{1}{N}\sum _{i=1}^N[y^{(i)}ln{h}_{\theta }(x^{(i)})+(1-y^{(i)})ln(1-h_{\theta }(x^{(i)}))]$$
则
$$▽J(\theta )=\frac{1}{N}\sum _{i=1}^N[h_{\theta }(x^{(i)})-y^{(i)}]x^{(i)}$$
$$\begin{array}{rl}H={▽}^{2}J(\theta )& =▽\frac{1}{N}\sum _{i=1}^N[h_{\theta }(x^{(i)})-y^{(i)}]x^{(i)}\\ & =▽\frac{1}{N}\sum _{i=1}^N{h}_{\theta }(x^{(i)})\cdot x^{(i)}\\ & =\frac{1}{N}\sum _{i=1}^N\frac{\partial h_{\theta }(x^{(i)})}{\partial \theta }\cdot (x^{(i)}{)}^T\\ & =\frac{1}{N}\sum _{i=1}^N{h}_{\theta }(x^{(i)}{)}^T\cdot (1-h_{\theta }(x^{(i)}))\cdot x^{(i)}\cdot (x^{(i)}{)}^T\end{array}$$
使用牛顿法更新权重：
$${\theta }^{(t+1)}:={\theta }^{(t)}-H^{-1}▽J(\theta )$$

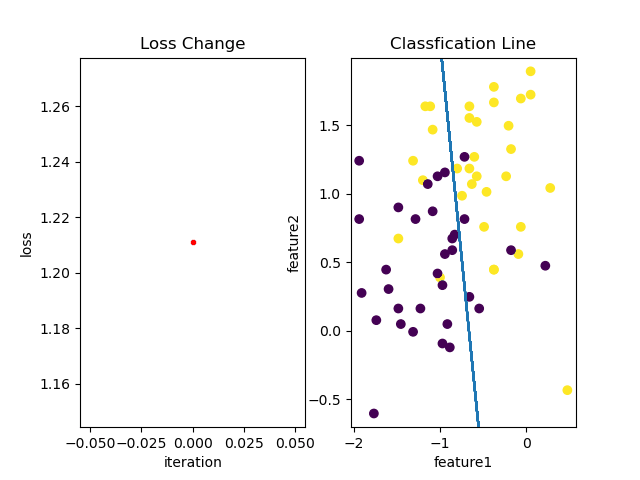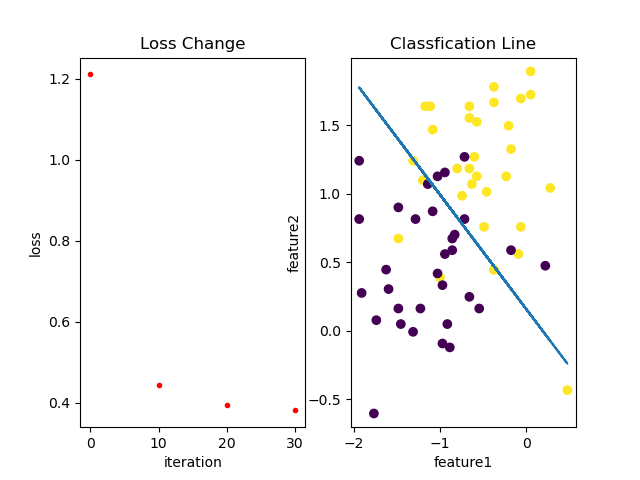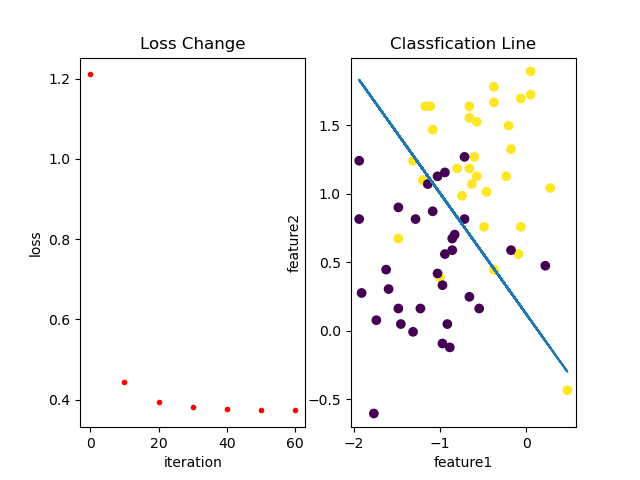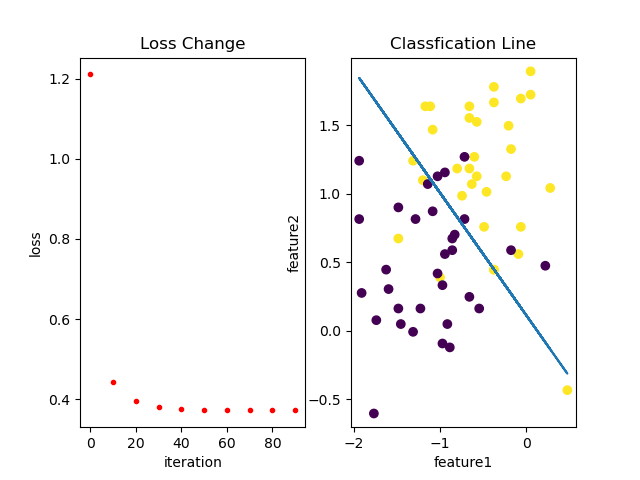
4、纯python实现

代码如下：

import numpy as np
import matplotlib.pyplot as plt
import time


# 加载数据
def load_data():
    X_train = np.loadtxt("./Exam/train/x.txt")
    Y_train = np.loadtxt("./Exam/train/y.txt", dtype=int)
    X_test = np.loadtxt("./Exam/test/x.txt")
    Y_test = np.loadtxt("./Exam/test/y.txt", dtype=int)
    return X_train, Y_train, X_test, Y_test


# Logistic回归类
class Logistic(object):
    def __init__(self, X_train, Y_train):
        self.X_train = X_train
        self.Y_train = Y_train
        # M:特征数，N：样本数
        self.M = X_train.shape[1]
        self.N = X_train.shape[0]
        self.train()

    def normalization(self):
        # 均值方差归一化
        mean = np.mean(self.X_train)
        variance = np.std(self.X_train)
        self.X_train = (self.X_train - mean)/variance
        self.X_train = np.insert(self.X_train, 0, values=1.0, axis=1)
        self.Y_train = self.Y_train.reshape(self.N, 1)
        self.M += 1
        
    def sigmoid(self, X):
        eta = -np.dot(X, self.theta)  # N*1
        H = np.exp(eta)
        H = 1.0 / (1.0 + H)
        return H

    def Newton_method(self):
        self.theta = -np.ones((self.M, 1))
        for i in range(100):
            self.H = self.sigmoid(self.X_train)
            self.J = np.dot(self.X_train.T, (self.H - self.Y_train))  #M*1
            self.Hession = np.dot(self.H.T, self.X_train).dot(self.X_train.T).dot((1.0 - self.H)) / self.N
            self.theta -= np.dot(self.J, np.linalg.inv(self.Hession))
            self.loss = -np.sum(self.Y_train * np.log(self.H) + (1.0 - self.Y_train)* np.log(1 - self.H))/self.N
            print("iter: %d, loss: %f" % (i, self.loss))
        print(self.theta)

    def train(self):
        self.normalization()
        self.Newton_method()


if __name__ == "__main__":
    X_train, Y_train, X_test, Y_test = load_data()
    Logistic(X_train, Y_train)    

训练过程中loss变化以及分类效果如下：

(自己学习机器学习的笔记，如有错误望提醒修正）