多重共线性检验之方差膨胀因子VIF
过程
1、构造每一个自变量与其余自变量的线性回归模型,例如,数 据集中含有p个自变量,则第一个自变量与其余自变量的线性组合可以 表示为
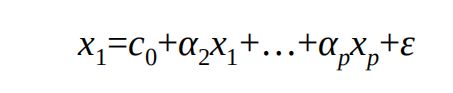
2、根据如上线性回归模型得到相应的判决系数 R 2 R^2 R2,进而计算第 一个自变量的方差膨胀因子VIF:

import pandas as pd
import numpy as np
from sklearn import model_selection
import statsmodels.api as sn
from statsmodels.stats.outliers_influence import variance_inflation_factor
sdata = pd.read_csv("../input/traindatas/char7/Predict to Profit.csv")
print(sdata.columns)
X = sn.add_constant(sdata.loc[:,['RD_Spend', 'Marketing_Spend']])
vif = pd.DataFrame()
vif["Ficture"] = X.columns
vif["Fctor"] = [variance_inflation_factor(X.values,i) for i in range(X.shape[1])]
print(vif)
执行结果如下,如上结果所示,两个自变量对应的方差膨胀因子均低于10,说明构 建模型的数据并不存在多重共线性。如果发现变量之间存在多重共线性 的话,可以考虑删除变量或者重新选择模型
Index(['RD_Spend', 'Administration', 'Marketing_Spend', 'State', 'Profit'], dtype='object')
Ficture Fctor
0 const 4.540984
1 RD_Spend 2.026141
2 Marketing_Spend 2.026141
过程计算
import pandas as pd
import numpy as np
from sklearn import model_selection
import statsmodels.api as sn
from statsmodels.stats.outliers_influence import variance_inflation_factor
sdata = pd.read_csv("../input/traindatas/char7/Predict to Profit.csv")
model = sn.formula.ols("RD_Spend~Marketing_Spend",data=sdata).fit()
print(1/(1-model.rsquared))
执行结果
2.026140603233619
上面我仅仅计算了以RD_Spend为因变量计算的VIF值,和上面的一样,为2.026140603233619