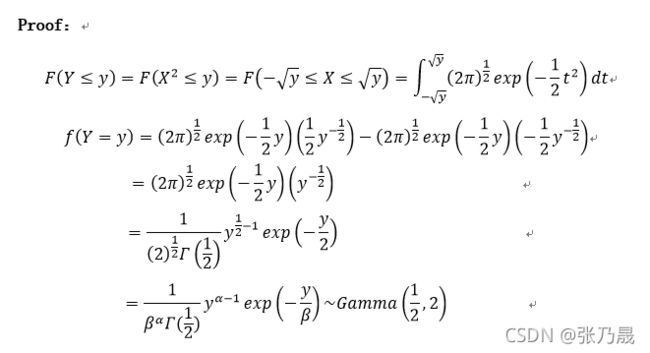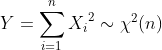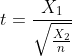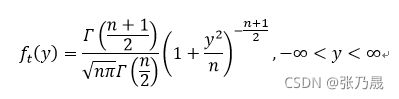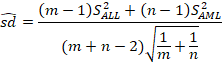置换检验及其R代码实现
目录
0.前言
1.基础回顾
1.1卡方分布与t分布
1.1.1自由度为1的卡方分布
1.1.2自由度为n的卡方分布
1.1.3t分布
1.2Fisher定理
1.3两样本t检验
1.4置换检验
2.案例
2.1问题背景
2.2经典两样本t检验
2.3置换检验
3.小结
4.参考资料
0.前言
本文将系统梳理《计算机时代的统计推断:算法、演化和数据科学》4.4节提到的置换检验(Permutation Test),给出必要的前行知识并对原书的案例进行代码实现。
1.基础回顾
1.1卡方分布与t分布
1.1.1自由度为1的卡方分布
如果随机变量![]() ,则随机变量
,则随机变量![]() ,其概率密度函数为
,其概率密度函数为
1.1.2自由度为n的卡方分布
设随机变量![]() 独立同分布于
独立同分布于![]() ,则
,则
1.1.3t分布
设随机变量![]() 相互独立且
相互独立且![]() ,
,![]() ,则称统计量
,则称统计量
服从自由度为n的t分布,记为![]() 。其概率密度函数为
。其概率密度函数为
注意:当自由度比较大(≥30 )时,t分布可以用标准正态分布近似。
1.2Fisher定理
1.3两样本t检验
根据t分布的定义和Fisher定理,可得两样本t检验的统计量,证明如下
1.4置换检验
置换检验(Permutation test)是Fisher于20世纪30年代提出的一种基于大量计算(computationally intensive),利用样本数据的全(或随机)排列,进行统计推断的方法,因其对总体分布自由,应用较为广泛,特别适用于总体分布未知的小样本资料,以及某些难以用常规方法分析资料的假设检验问题。在具体使用上它和Bootstrap Methods类似,通过对样本进行顺序上的置换,重新计算统计检验量,构造经验分布,然后在此基础上求出P-value进行推断。
本文需要用到的置换检验算法:
Step1:计算原始样本的检验统计量
Step2:将两组样本混合后随机生成足够多的类似样本并计算检验统计量
Step3:构造经验分布,计算大于原始样本检验统计量的p-value并将其和给定的显著性水平比较,进而得出结论。
2.案例
2.1问题背景
实验室对72名白血病患者的7128个基因组的遗传活性进行了测量,其中47名白血病患者为急性淋巴细胞白血病(ALL),25名为急性髓样白血病(AML)。下图显示了两组中基因136的遗传活性。
# 数据准备
leukemia = read.csv('C:/Users/suface/Desktop/研究生课程/Theory and Method of Statistics/ch4补充/置换检验/leukemia_big.csv')
X = leukemia[136,]
isALL = (substr(names(X), 1, 3) == 'ALL') # 将X的names的前三个字符截取出来(保证得到的都是ALL和AML的格式)
X_ALL = as.numeric(X[isALL])
X_AML = as.numeric(X[!isALL])
# 136号基因活性直方图
par(mfrow = c(2, 1), mar = c(4, 3, 3, 2.1))
hist(X_ALL, xlim = c(0.2, 1.6),xlab = 'ALL-mean 0.752', ylab = 'frequency', col = 'yellow', main = NULL)
hist(X_AML, xlab = 'AML-mean 0.950', ylab = 'frequency', col = 'red', main = NULL)可以看到AML组似乎显示出了更大的活性,两组的均值分别为
![]()
2.2经典两样本t检验
从统计学角度说明两者的基因活性是否有显著差异,经典方法是使用两样本的t检验。即构造如下双侧检验
![]()
检验统计量为
其中![]() 为两组的联合方差
为两组的联合方差
# 两样本t检验
m = length(X_ALL)
n = length(X_AML)
mu_ALL = mean(X_ALL)
mu_AML = mean(X_AML)
sd_joint = sqrt((sum((X_ALL - mu_ALL)^2) + sum((X_AML - mu_AML) ^ 2)) * (m + n) / (m * n * (n + m -2)))
t_h0 = (mu_ALL - mu_AML) / sd_joint
p_v = 2 * pt(t_h0, m + n - 2) # 计算双侧显著性可以算得
![]()
如果选定显著性水平![]() ,则由于
,则由于![]() ,可以拒绝原假设,认为两组的136基因活性表达有显著差异。
,可以拒绝原假设,认为两组的136基因活性表达有显著差异。
2.3置换检验
上述检验虽然经典,但常常因为过分依赖于正态抽样假设而面临质疑与批评。为了规避正态的前提假设,Fisher提出了置换检验,即将上述72个值随机划分为大小为47和25的不相交集合,重新计算两样本t统计量,重复进行![]() 次实验,得到排列{t1*,…,tB*} ,原始t值的双侧排列显著性水平可以通过下式计算
次实验,得到排列{t1*,…,tB*} ,原始t值的双侧排列显著性水平可以通过下式计算
![]()
即排列中t统计量超过原始t统计量的个数占全排列的总个数的比例。
# 置换检验
Y = as.numeric(X)
B = 10000
t_h0_B = rep(NA, B) # 生成一个逻辑型数据向量以遍存储后续生成的t统计量
set.seed(124)
for (b in 1:B){
idx = sample.int(n + m, m) # 从72个数中抽出47个数字
xb1 = Y[idx] # 取出上一步随机生成的idx对应的样本点
xb2 = Y[-idx] # 取出剩下的样本点
mu_xb1 = mean(xb1)
mu_xb2 = mean(xb2)
sd_joint_b = sqrt((sum((xb1- mu_xb1)^2) + sum((xb2 - mu_xb2) ^ 2)) * (m + n) / (m * n * (n + m -2)))
t_h0_B[b] = (mu_xb1 - mu_xb2) / sd_joint_b
}
p_vB = mean(abs(t_h0_B) > abs(t_h0))
par(mfrow = c(1,1))
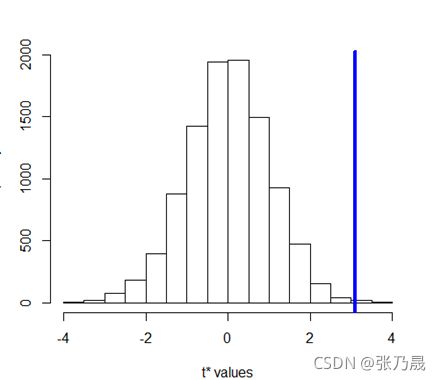
hist(t_h0_B, xlab = 't* values', main = NULL)
abline(v=3.1,lwd=4,col="blue")
生成的10000个t值中有23个大于了原始t值,
![]()
故可以拒绝原假设,认为两组的136基因活性表达有显著差异。
3.小结
无论是正态分布假设下的参数检验还是置换检验都计算了统计量,但是前者是跟理论分布进行比较,后者是跟置换观测数据后获得的经验分布进行比较。置换检验对总体分布自由,特别适合用于总体分布未知的小样本数据,以及一些常规方法难以使用的假设检验情况。
4.参考资料
[1] Efron B , Hastie T . Computer age statistical inference : algorithms, evidence, and data science. Cambridge University Press, 2016.
[2]茆诗松, 周纪芗. 概率论与数理统计 (第二版)[M]. 中国统计出版社, 2000.
[3] http://bcs.whfreeman.com/ips5e/content/cat_080/pdf/moore14.pdf
[4] http://jpkc.njmu.edu.cn/course/tongjixue/file/jxzy/tjjz02.htm
[5] http://www.r-bloggers.com/lang/chinese/541
[6] Permutation Test 置换检验 | Public Library of Bioinformatics
案例数据的下载地址:Computer Age Statistical Inference: Algorithms, Evidence and Data Science