【机器学习的数学基础】(七)矩阵分解(Matrix Decomposition)(中)
文章目录
-
- 4 矩阵分解(Matrix Decomposition)(中)
-
- 4.3 Cholesky分解
- 4.4 特征分解与对角化
- 4.5 奇异值分解
-
- 4.5.1 几何图解SVD
- 4.5.2 SVD的构建
- 4.5.3 特征值分解 vs. 奇异值分解
4 矩阵分解(Matrix Decomposition)(中)
4.3 Cholesky分解
在机器学习中,有许多方法可以分解一些特殊的矩阵。例如对于对称正定矩阵(见3.2.3节),我们有许多类似于平方根运算的方法。Cholesky分解(Cholesky decomposition/Cholesky factorization)就是其中一种,且很有用。
定理 4.18 Cholesky分解
对称正定矩阵 A \boldsymbol{A} A可以分解为: A = L L ⊤ \boldsymbol{A}=\boldsymbol{L} \boldsymbol{L}^{\top} A=LL⊤,其中 L \boldsymbol{L} L是具有正对角元素的下三角矩阵:
[ a 11 ⋯ a 1 n ⋮ ⋱ ⋮ a n 1 ⋯ a n n ] = [ l 11 ⋯ 0 ⋮ ⋱ ⋮ l n 1 ⋯ l n n ] [ l 11 ⋯ l n 1 ⋮ ⋱ ⋮ 0 ⋯ l n n ] \left[\begin{array}{ccc}a_{11} & \cdots & a_{1 n} \\\vdots & \ddots & \vdots \\a_{n 1} & \cdots & a_{n n}\end{array}\right]=\left[\begin{array}{ccc}l_{11} & \cdots & 0 \\\vdots & \ddots & \vdots \\l_{n 1} & \cdots & l_{n n}\end{array}\right]\left[\begin{array}{ccc}l_{11} & \cdots & l_{n 1} \\\vdots & \ddots & \vdots \\0 & \cdots & l_{n n}\end{array}\right] ⎣⎢⎡a11⋮an1⋯⋱⋯a1n⋮ann⎦⎥⎤=⎣⎢⎡l11⋮ln1⋯⋱⋯0⋮lnn⎦⎥⎤⎣⎢⎡l11⋮0⋯⋱⋯ln1⋮lnn⎦⎥⎤
L \boldsymbol{L} L被称为 A \boldsymbol{A} A的Cholesky因子( Cholesky factor),且是是唯一的。
例 4.10
考虑一个对称正定矩阵 A ∈ R 3 × 3 \boldsymbol{A} \in \mathbb{R}^{3 \times 3} A∈R3×3,我们要得到它的Cholesky分解 A = L L ⊤ \boldsymbol{A}=\boldsymbol{L} \boldsymbol{L}^{\top} A=LL⊤,即:
A = [ a 11 a 21 a 31 a 21 a 22 a 32 a 31 a 32 a 33 ] = L L ⊤ = [ l 11 0 0 l 21 l 22 0 l 31 l 32 l 33 ] [ l 11 l 21 l 31 0 l 22 l 32 0 0 l 33 ] \boldsymbol{A}=\left[\begin{array}{lll}a_{11} & a_{21} & a_{31} \\a_{21} & a_{22} & a_{32} \\a_{31} & a_{32} & a_{33}\end{array}\right]=\boldsymbol{L} \boldsymbol{L}^{\top}=\left[\begin{array}{lll}l_{11} & 0 & 0 \\l_{21} & l_{22} & 0 \\l_{31} & l_{32} & l_{33}\end{array}\right]\left[\begin{array}{ccc}l_{11} & l_{21} & l_{31} \\0 & l_{22} & l_{32} \\0 & 0 & l_{33}\end{array}\right] A=⎣⎡a11a21a31a21a22a32a31a32a33⎦⎤=LL⊤=⎣⎡l11l21l310l22l3200l33⎦⎤⎣⎡l1100l21l220l31l32l33⎦⎤
计算右边的矩阵相乘得到:
A = [ l 11 2 l 21 l 11 l 31 l 11 l 21 l 11 l 21 2 + l 22 2 l 31 l 21 + l 32 l 22 l 31 l 11 l 31 l 21 + l 32 l 22 l 31 2 + l 32 2 + l 33 2 ] \boldsymbol{A}=\left[\begin{array}{ccc}l_{11}^{2} & l_{21} l_{11} & l_{31} l_{11} \\l_{21} l_{11} & l_{21}^{2}+l_{22}^{2} & l_{31} l_{21}+l_{32} l_{22} \\l_{31} l_{11} & l_{31} l_{21}+l_{32} l_{22} & l_{31}^{2}+l_{32}^{2}+l_{33}^{2}\end{array}\right] A=⎣⎡l112l21l11l31l11l21l11l212+l222l31l21+l32l22l31l11l31l21+l32l22l312+l322+l332⎦⎤
比较等式两侧元素,可以看出对角线元素 l i i l_{ii} lii中有一个简单的规则:
l 11 = a 11 , l 22 = a 22 − l 21 2 , l 33 = a 33 − ( l 31 2 + l 32 2 ) l_{11}=\sqrt{a_{11}}, \quad l_{22}=\sqrt{a_{22}-l_{21}^{2}}, \quad l_{33}=\sqrt{a_{33}-\left(l_{31}^{2}+l_{32}^{2}\right)} l11=a11,l22=a22−l212,l33=a33−(l312+l322)
类似地,对于对角线以下的元素( l i j l_{ij} lij,其中 i > j i\gt j i>j),也存在规则:
l 21 = 1 l 11 a 21 , l 31 = 1 l 11 a 31 , l 32 = 1 l 22 ( a 32 − l 31 l 21 ) l_{21}=\frac{1}{l_{11}} a_{21}, \quad l_{31}=\frac{1}{l_{11}} a_{31}, \quad l_{32}=\frac{1}{l_{22}}\left(a_{32}-l_{31} l_{21}\right) l21=l111a21,l31=l111a31,l32=l221(a32−l31l21)
因此,我们构造了任意对称正定3×3矩阵的Cholesky分解。实现的关键是给定 A \boldsymbol{A} A的值 a i j a_{ij} aij和计算得到的 l i j l_{ij} lij,我们可以推算 L \boldsymbol{L} L的其他量。
Cholesky分解是机器学习中数值计算的重要工具。特别是在对称正定矩阵需要频繁的操作的时候,例如,多元高斯变量的协方差矩阵(概率与分布6.5节)是对称且正定的。这个协方差矩阵的Cholesky分解允许我们从高斯分布生成样本。它还允许我们对随机变量进行线性变换,这在计算深度随机模型(如变分自动编码器)中的梯度时被广泛使用。Cholesky分解还允许我们非常高效地计算行列式。给定Cholesky分解 A = L L ⊤ \boldsymbol{A}=\boldsymbol{L} \boldsymbol{L}^{\top} A=LL⊤,我们知道 det ( A ) = det ( L ) det ( L ⊤ ) = det ( L ) 2 \operatorname{det}(\boldsymbol{A})=\operatorname{det}(\boldsymbol{L}) \operatorname{det}\left(\boldsymbol{L}^{\top}\right)=\operatorname{det}(\boldsymbol{L})^{2} det(A)=det(L)det(L⊤)=det(L)2。因为 L \boldsymbol{L} L是三角矩阵,其行列式是它的对角线项的乘积 det ( A ) = ∏ i l i i 2 \operatorname{det}(\boldsymbol{A})=\prod_{i} l_{i i}^{2} det(A)=∏ilii2。因此,许多数值软件包使用Cholesky分解来提高计算效率。
4.4 特征分解与对角化
对角矩阵(diagonal matrix)是所有非对角元素的值为零的矩阵,即它们的形式为:
D = [ c 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ c n ] \boldsymbol{D}=\left[\begin{array}{ccc}c_{1} & \cdots & 0 \\\vdots & \ddots & \vdots \\0 & \cdots & c_{n}\end{array}\right] D=⎣⎢⎡c1⋮0⋯⋱⋯0⋮cn⎦⎥⎤
它们允许快速计算行列式、幂和逆。其行列式是其对角线项的乘积,矩阵的幂 D k \boldsymbol{D}^k Dk由每个对角线元素的 k k k次幂表示,如果所有对角线元素都不为零,则逆 D − 1 \boldsymbol{D}^{-1} D−1是对角线元素的倒数。
在本节中,我们将讨论如何将矩阵转换为对角线形式。这是我们2.72节中的基变化和4.2节的特征值的一个重要应用。
回想一下,如果存在可逆矩阵 P \boldsymbol{P} P,使得 D = P − 1 A P \boldsymbol{D}=\boldsymbol{P}^{-1} \boldsymbol{A P} D=P−1AP,则称矩阵 A \boldsymbol{A} A、 D \boldsymbol{D} D是相似的(定义2.22)。更具体地说,我们将研究矩阵 A \boldsymbol{A} A,它相似于对角线元素为 A \boldsymbol{A} A的特征值的对角矩阵 D \boldsymbol{D} D。
定义 4.19 可对角化矩阵
矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n如果相似于对角矩阵,则称它是可对角化的,即存在可逆矩阵 P ∈ R n × n \boldsymbol{P} \in \mathbb{R}^{n \times n} P∈Rn×n,使得 D = P − 1 A P \boldsymbol{D}=\boldsymbol{P}^{-1} \boldsymbol{A} \boldsymbol{P} D=P−1AP
在下文中,我们将看到矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的对角化实际是在另一个基中表示相同线性映射的一种方法,这个基由 A \boldsymbol{A} A的特征向量组成。
对于矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n,标量 λ 1 , … , λ n \lambda_{1}, \ldots, \lambda_{n} λ1,…,λn以及 R n \mathbb{R}^{n} Rn中的向量 p 1 , … , p n \boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n} p1,…,pn。我们定义 P : = [ p 1 , … , p n ] \boldsymbol{P}:=\left[\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n}\right] P:=[p1,…,pn]并令 D ∈ R n × n \boldsymbol{D} \in \mathbb{R}^{n \times n} D∈Rn×n为对角矩阵,对角元素为 λ 1 , … , λ n \lambda_{1}, \ldots, \lambda_{n} λ1,…,λn,那么我们可以证明
A P = P D \boldsymbol{A}\boldsymbol{P}=\boldsymbol{P}\boldsymbol{D} AP=PD
成立当且仅当 λ 1 , … , λ n \lambda_{1}, \ldots, \lambda_{n} λ1,…,λn为 A \boldsymbol{A} A的特征值, p 1 , … , p n \boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n} p1,…,pn为相应的 A \boldsymbol{A} A的特征向量。
这个结论成立是因为:
A P = A [ p 1 , … , p n ] = [ A p 1 , … , A p n ] \boldsymbol{A} \boldsymbol{P}=\boldsymbol{A}\left[\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n}\right]=\left[\boldsymbol{A} \boldsymbol{p}_{1}, \ldots,\boldsymbol{A} \boldsymbol{p}_{n}\right] AP=A[p1,…,pn]=[Ap1,…,Apn]
P D = [ p 1 , … , p n ] [ λ 1 0 ⋱ 0 λ n ] = [ λ 1 p 1 , … , λ n p n ] \boldsymbol{P} \boldsymbol{D}=\left[\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n}\right]\left[\begin{array}{ccc}\lambda_{1} & & 0 \\& \ddots & \\0 & & \lambda_{n}\end{array}\right]=\left[\lambda_{1} \boldsymbol{p}_{1}, \ldots, \lambda_{n} \boldsymbol{p}_{n}\right] PD=[p1,…,pn]⎣⎡λ10⋱0λn⎦⎤=[λ1p1,…,λnpn]
则 A P = P D \boldsymbol{A}\boldsymbol{P}=\boldsymbol{P}\boldsymbol{D} AP=PD意味着:
A p 1 = λ 1 p 1 ⋮ A p n = λ n p n \begin{aligned}\boldsymbol{A} \boldsymbol{p}_{1} &=\lambda_{1} \boldsymbol{p}_{1} \\& \vdots \\\boldsymbol{A p}_{n} &=\lambda_{n} \boldsymbol{p}_{n}\end{aligned} Ap1Apn=λ1p1⋮=λnpn
因此, P \boldsymbol{P} P的列必须为 A \boldsymbol{A} A的特征向量。
我们的定理要求 P ∈ R n × n \boldsymbol{P} \in \mathbb{R}^{n \times n} P∈Rn×n是可逆的,即 P \boldsymbol{P} P是满秩的(定理4.3),这需要 n n n个线性独立的特征向量 p 1 , … , p n \boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{n} p1,…,pn,即 p i \boldsymbol{p}_{i} pi形成 R n \mathbb{R}^n Rn的基。
定理 4.20特征分解 (Eigendecomposition)
方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n可以被分解为:
A = P D P − 1 \boldsymbol{A}=\boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1} A=PDP−1
其中 P ∈ R n × n \boldsymbol{P} \in \mathbb{R}^{n \times n} P∈Rn×n, D \boldsymbol{D} D为对角矩阵且对角元素为 A \boldsymbol{A} A的特征值,当且仅当 A \boldsymbol{A} A的特征向量形成 R n \mathbb{R}^n Rn的基。
定理4.20意味着只有非亏损矩阵才可以对角化,并且 P \boldsymbol{P} P的列是 A \boldsymbol{A} A的 n n n个特征向量。对于对称矩阵,我们可以得到更好的特征值分解结果。
定理 4.21
对称矩阵 S ∈ R n × n \boldsymbol{S} \in \mathbb{R}^{n \times n} S∈Rn×n可以被对角化。
定理4.21是承接谱定理(定理4.15)的。谱定理指出,对于对称矩阵,我们可以找到一个关于 R n \mathbb{R}^{n } Rn的特征向量的标准正交基(ONB)。这使得 P \boldsymbol{P} P是一个正交矩阵,因此 D = P ⊤ A P \boldsymbol{D}=\boldsymbol{P}^{\top} \boldsymbol{A P} D=P⊤AP。
备注:
矩阵的Jordan标准型提供了一种分解方法,它适用于亏损矩阵,但超出了本书的范围。
图解特征分解:
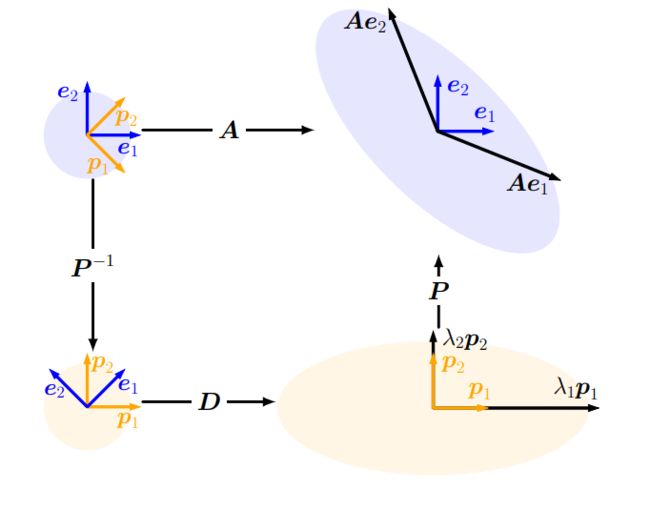
图 4.7特征分解背后的直观感觉是一系列变换。从左上角到左下角: P − 1 \boldsymbol{P}^{−1} P−1执行从标准基到特征基的基变化(这里在 R 2 \mathbb{R}^2 R2中绘制,并描述为类似旋转的操作)。从左下角到右下角: D \boldsymbol{D} D使得沿着映射的正交特征向量进行缩放,这里用一个被拉伸成椭圆的圆来描述。从右下到右上: P \boldsymbol{P} P撤消基变化(描述为反向旋转)并恢复原来的坐标系。
我们可以如下解释矩阵的特征分解(参见图4.7):
设 A \boldsymbol{A} A是相对于标准基的线性映射的变换矩阵( P − 1 = P − 1 I \boldsymbol{P}^{-1}=\boldsymbol{P}^{-1}\boldsymbol{I} P−1=P−1I)。 P − 1 \boldsymbol{P}^{-1} P−1执行从标准基到特征基的基变换。它将特征向量 p i \boldsymbol{p}_i pi(图中的蓝色和橙色箭头)标识到标准基向量 e i \boldsymbol{e}_i ei上。对角矩阵 D \boldsymbol{D} D通过特征值 λ i λ_i λi沿这些轴缩放向量。得到 λ i p i \lambda_{i} \boldsymbol{p}_{i} λipi的同时, P \boldsymbol{P} P将这些缩放向量转换回标准/规范坐标。
.
例 4.11 特征分解
让我们来计算 A = 1 2 [ 5 − 2 − 2 5 ] \boldsymbol{A}=\frac{1}{2}\left[\begin{array}{cc}5 & -2 \\-2 & 5\end{array}\right] A=21[5−2−25]的特征分解。
Step 1 计算特征值和特征向量
A \boldsymbol{A} A的特征方程为:
det ( A − λ I ) = det ( [ 5 2 − λ − 1 − 1 5 2 − λ ] ) = ( 5 2 − λ ) 2 − 1 = λ 2 − 5 λ + 21 4 = ( λ − 7 2 ) ( λ − 3 2 ) \begin{array}{l}\operatorname{det}(\boldsymbol{A}-\lambda \boldsymbol{I})=\operatorname{det}\left(\left[\begin{array}{lc}\frac{5}{2}-\lambda & -1 \\-1 & \frac{5}{2}-\lambda\end{array}\right]\right) \\=\left(\frac{5}{2}-\lambda\right)^{2}-1=\lambda^{2}-5 \lambda+\frac{21}{4}=\left(\lambda-\frac{7}{2}\right)\left(\lambda-\frac{3}{2}\right)\end{array} det(A−λI)=det([25−λ−1−125−λ])=(25−λ)2−1=λ2−5λ+421=(λ−27)(λ−23)
因此 A \boldsymbol{A} A的特征值为 λ 1 = 7 2 \lambda_{1}=\frac{7}{2} λ1=27和 λ 2 = 3 2 \lambda_{2}=\frac{3}{2} λ2=23(特征方程的根),并通过
[ 2 1 1 2 ] p 1 = 7 2 p 1 , [ 2 1 1 2 ] p 2 = 3 2 p 2 \left[\begin{array}{ll}2 & 1 \\1 & 2\end{array}\right] \boldsymbol{p}_{1}=\frac{7}{2} \boldsymbol{p}_{1}, \quad\left[\begin{array}{ll}2 & 1 \\1 & 2\end{array}\right] \boldsymbol{p}_{2}=\frac{3}{2} \boldsymbol{p}_{2} [2112]p1=27p1,[2112]p2=23p2
得到相应的特征向量:
p 1 = 1 2 [ 1 − 1 ] , p 2 = 1 2 [ 1 1 ] \boldsymbol{p}_{1}=\frac{1}{\sqrt{2}}\left[\begin{array}{c}1 \\-1\end{array}\right], \quad \boldsymbol{p}_{2}=\frac{1}{\sqrt{2}}\left[\begin{array}{l}1 \\1\end{array}\right] p1=21[1−1],p2=21[11]
Step 2 检查是否存在
p 1 , p 2 \boldsymbol{p}_{1},\boldsymbol{p}_{2} p1,p2形成 R 2 \mathbb{R}^2 R2的基,所以 A \boldsymbol{A} A可对角化。
Step 3 构造矩阵 P \boldsymbol{P} P使 A \boldsymbol{A} A对角化
P = [ p 1 , p 2 ] = 1 2 [ 1 1 − 1 1 ] \boldsymbol{P}=\left[\boldsymbol{p}_{1}, \boldsymbol{p}_{2}\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & 1 \\-1 & 1\end{array}\right] P=[p1,p2]=21[1−111]
然后我们得到:
P − 1 A P = [ 7 2 0 0 3 2 ] = D \boldsymbol{P}^{-1} \boldsymbol{A} \boldsymbol{P}=\left[\begin{array}{ll}\frac{7}{2} & 0 \\0 & \frac{3}{2}\end{array}\right]=\boldsymbol{D} P−1AP=[270023]=D
等价地,我们得到( P − 1 = P ⊤ \boldsymbol{P}^{-1}=\boldsymbol{P}^{\top} P−1=P⊤因为 p 1 , p 2 \boldsymbol{p}_1,\boldsymbol{p}_2 p1,p2可以形成ONB)
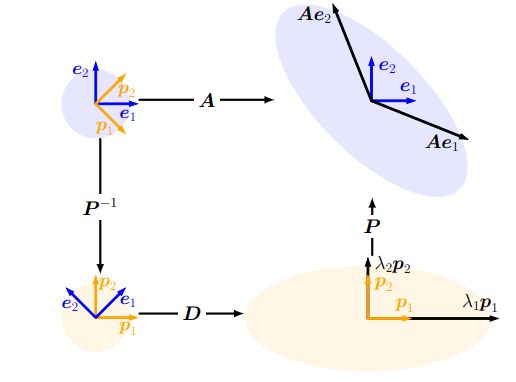
1 2 [ 5 − 2 − 2 5 ] ⏟ A = 1 2 [ 1 1 − 1 1 ] ⏟ P [ 7 2 0 0 3 2 ] ⏟ D 1 2 [ 1 − 1 1 1 ] ⏟ P − 1 \underbrace{\frac{1}{2}\left[\begin{array}{cc}5 & -2 \\-2 & 5\end{array}\right]}_{A}=\underbrace{\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & 1 \\-1 & 1\end{array}\right]}_{P} \underbrace{\left[\begin{array}{cc}\frac{7}{2} & 0 \\0 & \frac{3}{2}\end{array}\right]}_{D} \underbrace{\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & -1 \\1 & 1\end{array}\right]}_{P^{-1}} A 21[5−2−25]=P 21[1−111]D [270023]P−1 21[11−11]
整个变换过程如图:
-
对角矩阵 D \boldsymbol{D} D的幂可以被高效计算。因此,我们可以通过特征值分解(如果存在)计算矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的矩阵幂,即
A k = ( P D P − 1 ) k = P D k P − 1 \boldsymbol{A}^{k}=\left(\boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1}\right)^{k}=\boldsymbol{P} \boldsymbol{D}^{k} \boldsymbol{P}^{-1} Ak=(PDP−1)k=PDkP−1
计算 D k \boldsymbol{D}^{k} Dk是高效的,因为我们只需将此操作单独应用于所有对角线元素。 -
假设特征分解 A = P D P − 1 \boldsymbol{A}=\boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1} A=PDP−1存在,那么
det ( A ) = det ( P D P − 1 ) = det ( P ) det ( D ) det ( P − 1 ) = det ( D ) = ∏ i d i i \operatorname{det}(\boldsymbol{A})=\operatorname{det}\left(\boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1}\right)=\operatorname{det}(\boldsymbol{P}) \operatorname{det}(\boldsymbol{D}) \operatorname{det}\left(\boldsymbol{P}^{-1}\right)=\operatorname{det}(\boldsymbol{D})=\prod_{i} d_{i i} det(A)=det(PDP−1)=det(P)det(D)det(P−1)=det(D)=i∏dii
允许我们高效地计算 A \boldsymbol{A} A的行列式。
特征值分解需要该矩阵是方阵。在下一节中,我们将介绍一种更通用的矩阵分解技术,奇异值分解。
4.5 奇异值分解
矩阵奇异值分解( singular value decomposition, SVD)是线性代数中的一种核心的矩阵分解方法。它被称为“线性代数的基本定理”(Strang, 1993) ,因为它可以应用于所有矩阵,而不仅仅是方阵,而且总是存在的。此外,正如我们将在下文中探讨的,表示线性映射 Φ : V → W \Phi: V \rightarrow W Φ:V→W的矩阵 A \boldsymbol{A} A的奇异值分解量化了这两个向量空间的潜在几何变化。我们推荐Kalman(1996)和Roy和Banerjee(2014)的工作,以更深入地理解SVD。
定理 4.22 奇异值分解定理 (SVD Theorem)
令 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n为秩 r ∈ [ 0 , min ( m , n ) ] r \in[0, \min (m, n)] r∈[0,min(m,n)]的矩形矩阵。 A \boldsymbol{A} A奇异值分解的形式为:
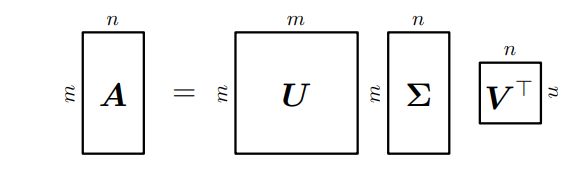
其中 U ∈ R m × m \boldsymbol{U} \in \mathbb{R}^{m \times m} U∈Rm×m为正交矩阵,其列向量为 u i , i = 1 , … , m \boldsymbol{u}_{i}, i=1, \ldots, m ui,i=1,…,m; V ∈ R m × m \boldsymbol{V} \in \mathbb{R}^{m \times m} V∈Rm×m也为正交矩阵,其列向量为 v i , i = 1 , … , n \boldsymbol{v}_{i}, i=1, \ldots, n vi,i=1,…,n;另外, Σ \boldsymbol{\Sigma} Σ为 m × n m\times n m×n矩阵, Σ i i = σ i ⩾ 0 \Sigma_{i i}=\sigma_{i} \geqslant 0 Σii=σi⩾0且, Σ i j = 0 , i ≠ j \Sigma_{i j}=0, i \neq j Σij=0,i=j
Σ \boldsymbol{\Sigma} Σ的对角元素 σ i , i = 1 , … , r \sigma_{i}, i=1, \ldots, r σi,i=1,…,r称为奇异值(singular values), u i \boldsymbol{u}_{i} ui称为右奇异向量(left-singular vectors), v i \boldsymbol{v}_{i} vi称为左奇异向量(right-singular vectors),按照惯例,奇异值是有序的,即 σ 1 ⩾ σ 2 ⩾ σ r ⩾ 0 \sigma_{1} \geqslant \sigma_{2} \geqslant\sigma_{r} \geqslant 0 σ1⩾σ2⩾σr⩾0。
奇异值矩阵 Σ \boldsymbol{\Sigma} Σ是唯一的。但需要注意的是 Σ ∈ R m × n \boldsymbol{\Sigma} \in \mathbb{R}^{m\times n} Σ∈Rm×n是矩形的。特别地, Σ \boldsymbol{\Sigma} Σ与 A \boldsymbol{A} A尺寸相同。这意味着 Σ \boldsymbol{\Sigma} Σ有一个包含奇异值的对角子矩阵而其他元素用零填充。具体而言,如果 m > n m\gt n m>n,那么 Σ \boldsymbol{\Sigma} Σ具有直到第 n n n行的对角线结构,然后从 n + 1 n+1 n+1行到 m m m行都是 0 ⊤ \boldsymbol{0}^{\top} 0⊤。
Σ = [ σ 1 0 0 0 ⋱ 0 0 0 σ n 0 … 0 ⋮ ⋮ 0 … 0 ] \boldsymbol{\Sigma}=\left[\begin{array}{ccc}\sigma_{1} & 0 & 0 \\0 & \ddots & 0 \\0 & 0 & \sigma_{n} \\0 & \ldots & 0 \\\vdots & & \vdots \\0 & \ldots & 0\end{array}\right] Σ=⎣⎢⎢⎢⎢⎢⎢⎢⎡σ1000⋮00⋱0……00σn0⋮0⎦⎥⎥⎥⎥⎥⎥⎥⎤
而如果 m < n m\lt n m<n,那么 Σ \boldsymbol{\Sigma} Σ具有直到第 m m m列的对角线结构,然后从 m + 1 m+1 m+1列到 n n n列都是 0 \boldsymbol{0} 0
Σ = [ σ 1 0 0 0 … 0 0 ⋱ 0 ⋮ ⋮ 0 0 σ m 0 … 0 ] \boldsymbol{\Sigma}=\left[\begin{array}{cccccc}\sigma_{1} & 0 & 0 & 0 & \ldots & 0 \\0 & \ddots & 0 & \vdots & & \vdots \\0 & 0 & \sigma_{m} & 0 & \ldots & 0\end{array}\right] Σ=⎣⎢⎡σ1000⋱000σm0⋮0……0⋮0⎦⎥⎤
备注:SVD对任意 A ⊂ R m × n \boldsymbol{A} \subset \mathbb{R}^{m \times n} A⊂Rm×n都成立。
4.5.1 几何图解SVD
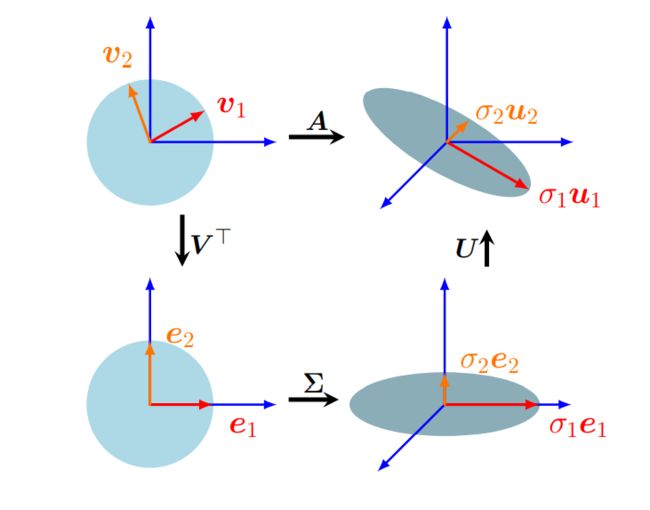
图 4.8 对矩阵 A ∈ R 3 × 2 \boldsymbol{A}∈\mathbb{R}^{3×2} A∈R3×2的SVD可用一系列变换直观理解。从左上角到左下角: V ⊤ \boldsymbol{V}^{\top} V⊤ 在 R 2 \mathbb{R}^2 R2中执行基的变化。左下角到右下角: Σ \boldsymbol{\Sigma} Σ缩放并从 R 2 \mathbb{R}^2 R2映射到 R 3 \mathbb{R}^3 R3。右下角的椭圆位于 R 3 \mathbb{R}^3 R3。第三维正交于椭圆盘的表面。右下角到右上角: U \boldsymbol{U} U在 R 3 \mathbb{R}^3 R3执行基变换。
奇异值分解提供了描述变换矩阵 A \boldsymbol{A} A的几何直观性。下面,我们将把奇异值分解作为在基上执行的一系列线性变换来讨论。在示例4.12中,我们将SVD的变换矩阵应用于 R 2 \mathbb{R}^2 R2中的一组向量,这使我们能够更清楚地看到每个变换的效果。
矩阵的奇异值分解可以解释为相应线性映射 Φ : R n → R m \Phi: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} Φ:Rn→Rm分解为三个运算;如图4.8所示。SVD直观上与我们的特征分解相似:广义地说,奇异值分解通过 V ⊤ \boldsymbol{V}^{\top} V⊤进行基变换,然后通过奇异值矩阵 Σ \boldsymbol{\Sigma} Σ进行尺度缩放和维数增加(或减少)。最后,它通过 U \boldsymbol{U} U执行第二个基变换。SVD包含许多重要的细节和注意事项,下面我们将更详细地解释:
1、矩阵 V \boldsymbol{V} V在域 R n \mathbb{R}^{n} Rn中执行从 B ~ \tilde{B} B~(由上图左上角的红色和橙色向量 v 1 \boldsymbol{v}_1 v1和 v 2 \boldsymbol{v}_2 v2表示)到标准基 B B B的基变换。 V ⊤ = V − 1 \boldsymbol{V}^{\top}=\boldsymbol{V}^{-1} V⊤=V−1执行从 B B B到 B ~ \tilde{B} B~的基变换。使得红色和橙色向量与图左下角的标准基对齐。
2、将坐标系改为 C ~ \tilde{C} C~的同时(书中的 B ~ \tilde{B} B~可能有误), Σ \boldsymbol{\Sigma} Σ用奇异值 σ i σ_i σi缩放新坐标(并增加或删除维度),即 Σ \boldsymbol{\Sigma} Σ是 Φ \Phi Φ相对于 B ~ \tilde{B} B~和 C ~ \tilde{C} C~的变换矩阵,表示为被拉伸并位于 e 1 − e 2 \boldsymbol{e}_1-\boldsymbol{e}_2 e1−e2平面上的红色和橙色矢量,它现在嵌入在图右下角的第三维中。
3、 U \boldsymbol{U} U在陪域 R m \mathbb{R}^{m} Rm中执行基变换,从 C ~ \tilde{C} C~变为 R m \mathbb{R}^{m} Rm的标准基,由 e 1 − e 2 \boldsymbol{e}_1-\boldsymbol{e}_2 e1−e2平面外的红色和橙色向量的旋转表示。如图4.8右上角所示。
SVD表示域和陪域(见线性代数中的像与核)的基变换。这与在同一向量空间中操作的特征分解形成对比:后者在相同的向量空间中应用相同的基变化,然后撤消。奇异值分解的特殊之处在于这两个不同的基同时被奇异值矩阵 Σ \boldsymbol{\Sigma} Σ连接起来。

图 4.9SVD和向量(用圆盘表示)的映射。与图4.8中的结构方向相反。
例 4.12 向量与奇异值分解
考虑正方形网格中向量 X ∈ R 2 \mathcal{X} \in \mathbb{R}^{2} X∈R2的一个映射,它嵌于以原点为中心大小为2×2的长方体。使用标准基,我们对这些向量进行映射:
A = [ 1 − 0.8 0 1 1 0 ] = U Σ V ⊤ = [ − 0.79 0 − 0.62 0.38 − 0.78 − 0.49 − 0.48 − 0.62 0.62 ] [ 1.62 0 0 1.0 0 0 ] [ − 0.78 0.62 − 0.62 − 0.78 ] \begin{aligned}\boldsymbol{A} &=\left[\begin{array}{cc}1 & -0.8 \\0 & 1 \\1 & 0\end{array}\right]=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top} \\&=\left[\begin{array}{ccc}-0.79 & 0 & -0.62 \\0.38 & -0.78 & -0.49 \\-0.48 & -0.62 & 0.62\end{array}\right]\left[\begin{array}{cc}1.62 & 0 \\0 & 1.0 \\0 & 0\end{array}\right]\left[\begin{array}{cc}-0.78 & 0.62 \\-0.62 & -0.78\end{array}\right]\end{aligned} A=⎣⎡101−0.810⎦⎤=UΣV⊤=⎣⎡−0.790.38−0.480−0.78−0.62−0.62−0.490.62⎦⎤⎣⎡1.620001.00⎦⎤[−0.78−0.620.62−0.78]
我们从排列在网格中的向量集合 X \mathcal{X} X(彩色点;参见图4.9的左上面板)开始。
我们应用 V ⊤ ∈ R 2 × 2 \boldsymbol{V}^{\top} \in \mathbb{R}^{2 \times 2} V⊤∈R2×2旋转 X \mathcal{X} X。旋转后的矢量显示在图4.9的左下角。我们现在使用奇异值矩阵 Σ \boldsymbol{\Sigma} Σ将这些向量映射到陪域 R 3 \mathbb{R}^3 R3(见图4.9右下角)。
请注意,所有向量都位于 x 1 − x 2 x_1-x_2 x1−x2平面中。第三个坐标总是0。 x 1 − x 2 x_1-x_2 x1−x2平面中的向量被奇异值拉伸。
向量集 X \mathcal{X} X通过 A \boldsymbol{A} A直接映射到配域 R 3 \mathbb{R}^3 R3等于 X \mathcal{X} X通过 U Σ V ⊤ \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V^{\top}} UΣV⊤的变换,其中 U \boldsymbol{U} U在配域 R 3 \mathbb{R}^3 R3内执行旋转,使得映射的向量不再局限于 x 1 − x 2 x_1-x_2 x1−x2平面;但它们仍然在一个平面上,如图4.9右上角。
4.5.2 SVD的构建
接下来我们将讨论SVD存在的原因,并详细说明如何计算它。一般矩阵的奇异值分解与方阵的特征分解有一些相似之处。
备注:
对称正定(SPD)矩阵的特征分解
S = S ⊤ = P D P ⊤ \boldsymbol{S}=\boldsymbol{S^{\top}}=\boldsymbol{P}\boldsymbol{D}\boldsymbol{P}^{\top} S=S⊤=PDP⊤
与相应的SVD做对比:
S = U Σ V ⊤ \boldsymbol{S}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top} S=UΣV⊤
如果我们令
U = P = V , D = Σ \boldsymbol{U}=\boldsymbol{P}=\boldsymbol{V}, \quad \boldsymbol{D}=\boldsymbol{\Sigma} U=P=V,D=Σ
我们看到SPD矩阵的奇异值分解就是特征分解。
接下来,我们将探讨定理4.22成立的原因以及奇异值分解是如何构造的。求 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n的奇异值分解等价于分别求陪域 R m \mathbb{R}^{m} Rm和陪域 R n \mathbb{R}^{n} Rn的两组正交基 U = ( u 1 , … , u m ) U=\left(\boldsymbol{u}_{1}, \ldots, \boldsymbol{u}_{m}\right) U=(u1,…,um)和 V = ( v 1 , … , v n ) V=\left(\boldsymbol{v}_{1}, \ldots, \boldsymbol{v}_{n}\right) V=(v1,…,vn)。根据这些有序基,我们将构造矩阵 U \boldsymbol{U} U和 V \boldsymbol{V} V。
让我们从构造右奇异向量开始。谱定理(定理4.15)告诉我们对称矩阵的特征向量形成一个标准正交基(ONB),这也意味着它可以对角化。此外,从定理4.14我们可以从任意矩形矩阵 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n构造对称的半正定矩阵 A ⊤ A ∈ R n × n \boldsymbol{A}^{\top} \boldsymbol{A} \in \mathbb{R}^{n \times n} A⊤A∈Rn×n。因此,我们总是可以对角化 A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A:
A ⊤ A = P D P ⊤ = P [ λ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ λ n ] P ⊤ ( 4.72 ) \boldsymbol{A}^{\top} \boldsymbol{A}=\boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{\top}=\boldsymbol{P}\left[\begin{array}{ccc}\lambda_{1} & \cdots & 0 \\\vdots & \ddots & \vdots \\0 & \cdots & \lambda_{n}\end{array}\right] \boldsymbol{P}^{\top}\qquad (4.72) A⊤A=PDP⊤=P⎣⎢⎡λ1⋮0⋯⋱⋯0⋮λn⎦⎥⎤P⊤(4.72)
其中 P \boldsymbol{P} P是正交矩阵,由正交特征基组成。 λ i ⩾ 0 \lambda_{i} \geqslant 0 λi⩾0为 A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A的特征值。假设 A \boldsymbol{A} A的SVD存在,则:
A ⊤ A = ( U Σ V ⊤ ) ⊤ ( U Σ V ⊤ ) = V Σ ⊤ U ⊤ U Σ V ⊤ \boldsymbol{A}^{\top} \boldsymbol{A}=\left(\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}\right)^{\top}\left(\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}\right)=\boldsymbol{V} \boldsymbol{\Sigma}^{\top} \boldsymbol{U}^{\top} \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top} A⊤A=(UΣV⊤)⊤(UΣV⊤)=VΣ⊤U⊤UΣV⊤
其中 U , V \boldsymbol{U},\boldsymbol{V} U,V为正交矩阵。因此,由 U ⊤ U = I \boldsymbol{U}^{\top} \boldsymbol{U}=\boldsymbol{I} U⊤U=I,我们得到:
A ⊤ A = V Σ ⊤ Σ V ⊤ = V [ σ 1 2 0 0 0 ⋱ 0 0 0 σ n 2 ] V ⊤ ( 4.73 ) \boldsymbol{A}^{\top} \boldsymbol{A}=\boldsymbol{V} \boldsymbol{\Sigma}^{\top} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}=\boldsymbol{V}\left[\begin{array}{ccc}\sigma_{1}^{2} & 0 & 0 \\0 & \ddots & 0 \\0 & 0 & \sigma_{n}^{2}\end{array}\right] \boldsymbol{V}^{\top}\qquad (4.73) A⊤A=VΣ⊤ΣV⊤=V⎣⎡σ12000⋱000σn2⎦⎤V⊤(4.73)
对比(4.72)和(4.73)两个式子,我们得到:
V ⊤ = P ⊤ \boldsymbol{V}^{\top}=\boldsymbol{P}^{\top} V⊤=P⊤
σ i 2 = λ i ( 4.75 ) \sigma_{i}^{2}=\lambda_{i}\qquad (4.75) σi2=λi(4.75)
因此,组成 P \boldsymbol{P} P的 A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A的特征向量是 A \boldsymbol{A} A的右奇异向量 V \boldsymbol{V} V。 A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A的特征值是 Σ \boldsymbol{\Sigma} Σ中奇异值的平方。
为了得到左奇异向量 U \boldsymbol{U} U,我们遵循类似的过程。我们首先计算对称矩阵 A A ⊤ ∈ R m × m \boldsymbol{A} \boldsymbol{A}^{\top} \in \mathbb{R}^{m \times m} AA⊤∈Rm×m(不是原来的 A ⊤ A ∈ R n × n \boldsymbol{A}^{\top} \boldsymbol{A} \in \mathbb{R}^{n \times n} A⊤A∈Rn×n)的奇异值分解
):
A A ⊤ = ( U Σ V ⊤ ) ( U Σ V ⊤ ) ⊤ = U Σ V ⊤ V Σ ⊤ U ⊤ \boldsymbol{A} \boldsymbol{A}^{\top}=\left(\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}\right)\left(\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top}\right)^{\top}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{\top} \boldsymbol{V} \boldsymbol{\Sigma}^{\top} \boldsymbol{U}^{\top} AA⊤=(UΣV⊤)(UΣV⊤)⊤=UΣV⊤VΣ⊤U⊤
= U [ σ 1 2 0 0 0 ⋱ 0 0 0 σ m 2 ] U ⊤ ( 4.76 b ) =\boldsymbol{U}\left[\begin{array}{ccc}\sigma_{1}^{2} & 0 & 0 \\0 & \ddots & 0 \\0 & 0 & \sigma_{m}^{2}\end{array}\right] \boldsymbol{U}^{\top} \qquad (4.76b) =U⎣⎡σ12000⋱000σm2⎦⎤U⊤(4.76b)
谱定理告诉我们, A A ⊤ = S D S ⊤ \boldsymbol{A} \boldsymbol{A}^{\top}=\boldsymbol{S} \boldsymbol{D} \boldsymbol{S}^{\top} AA⊤=SDS⊤可以对角化,我们可以找到 A A ⊤ \boldsymbol{A} \boldsymbol{A}^{\top} AA⊤的特征向量的标准正交基(ONB),这些特征向量组成 S \boldsymbol{S} S中。 A A ⊤ \boldsymbol{A} \boldsymbol{A}^{\top} AA⊤的正交特征向量是左奇异向量 U \boldsymbol{U} U,在奇异值分解的陪域中形成一个正交基。
由于 A A ⊤ \boldsymbol{A} \boldsymbol{A}^{\top} AA⊤和 A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A具有相同的非零特征值( 矩阵与其转置矩阵具有相同的特征值,但不一定具有相同的特征向量。),两种情况下的奇异值分解中 Σ \boldsymbol{\Sigma} Σ矩阵的非零项是相同的。
最后,我们把SVD各个部分联系起来。我们在 V \boldsymbol{V} V中有一个右奇异向量的正交集。为了完成奇异值分解的构造,我们将它们与正交向量 U \boldsymbol{U} U联系起来。为了达到这个目的,我们利用了 A \boldsymbol{A} A变换下 v i \boldsymbol{v}_i vi的像也必须是正交的这一事实(在3.4节中已经证明这一点)。对于 i ≠ j i\not =j i=j,我们要求 A v i \boldsymbol{A}\boldsymbol{v}_i Avi和 A v j \boldsymbol{A}\boldsymbol{v}_j Avj之间的内积必须为0。即对于任意两个正交向量 v i , v j , i ≠ j \boldsymbol{v}_i,\boldsymbol{v}_j,i\not =j vi,vj,i=j,以下成立:
( A v i ) ⊤ ( A v j ) = v i ⊤ ( A ⊤ A ) v j = v i ⊤ ( λ j v j ) = λ j v i ⊤ v j = 0 \left(\boldsymbol{A} \boldsymbol{v}_{i}\right)^{\top}\left(\boldsymbol{A} \boldsymbol{v}_{j}\right)=\boldsymbol{v}_{i}^{\top}\left(\boldsymbol{A}^{\top} \boldsymbol{A}\right) \boldsymbol{v}_{j}=\boldsymbol{v}_{i}^{\top}\left(\lambda_{j} \boldsymbol{v}_{j}\right)=\lambda_{j} \boldsymbol{v}_{i}^{\top} \boldsymbol{v}_{j}=0 (Avi)⊤(Avj)=vi⊤(A⊤A)vj=vi⊤(λjvj)=λjvi⊤vj=0
即对于 m ⩾ r m \geqslant r m⩾r, { A v 1 , … , A v r } \left\{\boldsymbol{A} \boldsymbol{v}_{1}, \ldots, \boldsymbol{A} \boldsymbol{v}_{r}\right\} { Av1,…,Avr}是 R m \mathbb{R}^\textcolor{blue}{m} Rm的 r r r维子空间的基成立。
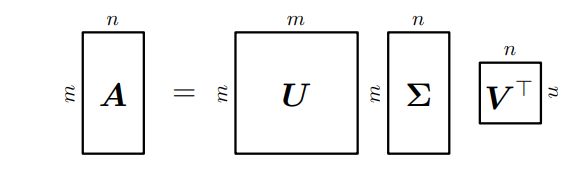
为了完成奇异值分解的构造,我们还需要左奇异向量是标准正交的:我们对右奇异向量 A v i \boldsymbol{A} \boldsymbol{v}_{i} Avi的像进行单位化,得到
u i : = A v i ∥ A v i ∥ = 1 λ i A v i = 1 σ i A v i ( 4.78 ) \boldsymbol{u}_{i}:=\frac{\boldsymbol{A} \boldsymbol{v}_{i}}{\left\|\boldsymbol{A} \boldsymbol{v}_{i}\right\|}=\frac{1}{\sqrt{\lambda_{i}}} \boldsymbol{A} \boldsymbol{v}_{i}=\frac{1}{\sigma_{i}} \boldsymbol{A} \boldsymbol{v}_{i}\qquad (4.78) ui:=∥Avi∥Avi=λi1Avi=σi1Avi(4.78)
其中,最后一个等式由(4.75)和(4.76b)求得
因此, A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A的特征向量,也即右奇异向量 v i \boldsymbol{v}_{i} vi,以及它们在 A \boldsymbol{A} A变换后的像归一化得到的左奇异向量 u i \boldsymbol{u}_{i} ui,分别形成两个标准正交基,它们通过奇异值矩阵 Σ \boldsymbol{\Sigma} Σ联系了起来。
让我们重新排列 (4.78) 公式,得到奇异值方程(singular value equation)
A v i = σ i u i , i = 1 , … , r ( 4.79 ) \boldsymbol{A} \boldsymbol{v}_{i}=\sigma_{i} \boldsymbol{u}_{i}, \quad i=1, \ldots, r\qquad (4.79) Avi=σiui,i=1,…,r(4.79)
这个方程与特征值方程 A x = λ x \boldsymbol{A} \boldsymbol{x}=\lambda \boldsymbol{x} Ax=λx非常相似,但是左边和右边的向量不一样。
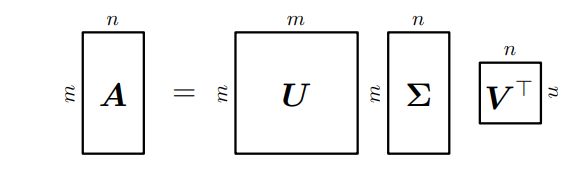
对于 n < m n\lt m n<m的 A \boldsymbol{A} A,奇异值方程 A v i = σ i u i \boldsymbol{A} \boldsymbol{v}_{i}=\sigma_{i} \boldsymbol{u}_{i} Avi=σiui只适用于 i ≤ n i\le n i≤n,对 i > n i\gt n i>n的 u i \boldsymbol{u}_{i} ui则不起作用。然而,通过构造我们知道它们是标准正交的。相反地,对于 m < n m\lt n m<n的 A \boldsymbol{A} A,奇异值方程只适用于 i ≤ m i\le m i≤m。对于 i > m i\gt m i>m, A v i = 0 \boldsymbol{A}\boldsymbol{v}_i=\boldsymbol{0} Avi=0,我们知道 v i \boldsymbol{v}_i vi形成了一个正交集。这意味着SVD还提供了 A \boldsymbol{A} A的核(零空间)的正交基,即 A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0的向量集 x \boldsymbol{x} x。
以 v i \boldsymbol{v}_i vi为列组合成 V \boldsymbol{V} V,以 u i \boldsymbol{u}_i ui为列组合成 U \boldsymbol{U} U,得到:
A V = U Σ \boldsymbol{A} \boldsymbol{V}=\boldsymbol{U} \boldsymbol{\Sigma} AV=UΣ
式中, Σ \boldsymbol{\Sigma} Σ的尺寸与 A \boldsymbol{A} A相同, 1 , … , r 1, \ldots, r 1,…,r行为对角线结构。右乘 V ⊤ \boldsymbol{V}^{\top} V⊤产生 A = U Σ V ⊤ \boldsymbol{A}=\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{V}^{\top} A=UΣV⊤,这是 A \boldsymbol{A} A的奇异值分解。
例 4.13 计算SVD
计算以下矩阵的SVD
A = [ 1 0 1 − 2 1 0 ] \boldsymbol{A}=\left[\begin{array}{ccc}1 & 0 & 1 \\-2 & 1 & 0\end{array}\right] A=[1−20110]
奇异值分解需要我们计算右奇异向量 v j \boldsymbol{v}_j vj、奇异值 σ k σ_k σk和左奇异向量 u i \boldsymbol{u}_i ui
Step 1: A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A的特征基作为右奇异向量
首先,我们计算
A ⊤ A = [ 1 − 2 0 1 1 0 ] [ 1 0 1 − 2 1 0 ] = [ 5 − 2 1 − 2 1 0 1 0 1 ] \boldsymbol{A}^{\top} \boldsymbol{A}=\left[\begin{array}{cc}1 & -2 \\0 & 1 \\1 & 0\end{array}\right]\left[\begin{array}{ccc}1 & 0 & 1 \\-2 & 1 & 0\end{array}\right]=\left[\begin{array}{ccc}5 & -2 & 1 \\-2 & 1 & 0 \\1 & 0 & 1\end{array}\right] A⊤A=⎣⎡101−210⎦⎤[1−20110]=⎣⎡5−21−210101⎦⎤
我们通过 A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A的特征值分解计算奇异值和右奇异向量 v j \boldsymbol{v}_j vj,如下所示
A ⊤ A = [ 5 30 0 − 1 6 − 2 30 1 5 − 2 6 1 30 2 5 1 6 ] [ 6 0 0 0 1 0 0 0 0 ] [ 5 30 − 2 30 1 30 0 1 5 2 5 − 1 6 − 2 6 1 6 ] = P D P ⊤ \boldsymbol{A}^{\top} \boldsymbol{A}=\left[\begin{array}{ccc}\frac{5}{\sqrt{30}} & 0 & \frac{-1}{\sqrt{6}} \\\frac{-2}{\sqrt{30}} & \frac{1}{\sqrt{5}} & \frac{-2}{\sqrt{6}} \\\frac{1}{\sqrt{30}} & \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{6}}\end{array}\right]\left[\begin{array}{ccc}6 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 0\end{array}\right]\left[\begin{array}{ccc}\frac{5}{\sqrt{30}} & \frac{-2}{\sqrt{30}} & \frac{1}{\sqrt{30}} \\0 & \frac{1}{\sqrt{5}} & \frac{2}{\sqrt{5}} \\\frac{-1}{\sqrt{6}} & \frac{-2}{\sqrt{6}} & \frac{1}{\sqrt{6}}\end{array}\right]=\boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{\top} A⊤A=⎣⎢⎡30530−2301051526−16−261⎦⎥⎤⎣⎡600010000⎦⎤⎣⎢⎡30506−130−2516−23015261⎦⎥⎤=PDP⊤
我们得到作为 P \boldsymbol{P} P的列的右奇异向量,这样
V = P = [ 5 30 0 − 1 6 − 2 30 1 5 − 2 6 1 30 2 5 1 6 ] \boldsymbol{V}=\boldsymbol{P}=\left[\begin{array}{ccc}\frac{5}{\sqrt{30}} & 0 & \frac{-1}{\sqrt{6}} \\\frac{-2}{\sqrt{30}} & \frac{1}{\sqrt{5}} & \frac{-2}{\sqrt{6}} \\\frac{1}{\sqrt{30}} & \frac{2}{\sqrt{5}} & \frac{1}{\sqrt{6}}\end{array}\right] V=P=⎣⎢⎡30530−2301051526−16−261⎦⎥⎤
Step 2: 奇异值矩阵
由于奇异值 σ i \sigma_{i} σi是 A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A的特征值的平方根,我们可以直接从 D \boldsymbol{D} D得到它们。由于 rk ( A ) = 2 \operatorname{rk}(\boldsymbol{A})=2 rk(A)=2,只有两个非零奇异值: σ 1 = 6 \sigma_{1}=\sqrt{6} σ1=6和 σ 2 = 1 \sigma_{2}=1 σ2=1。奇异值矩阵的尺寸必须与 A \boldsymbol{A} A相同,我们得到
Σ = [ 6 0 0 0 1 0 ] \boldsymbol{\Sigma}=\left[\begin{array}{lll}\sqrt{6} & 0 & 0 \\0 & 1 & 0\end{array}\right] Σ=[600100]
Step3:左奇异向量作为右奇异向量像的归一化。
我们通过计算右奇异向量在 A \boldsymbol{A} A变换下的像,并将其除以相应的奇异值进行归一化,得到左奇异向量。我们获得
u 1 = 1 σ 1 A v 1 = 1 6 [ 1 0 1 − 2 1 0 ] [ 5 30 − 2 30 1 30 ] = [ 1 5 − 2 5 ] \boldsymbol{u}_{1}=\frac{1}{\sigma_{1}} \boldsymbol{A} \boldsymbol{v}_{1}=\frac{1}{\sqrt{6}}\left[\begin{array}{ccc}1 & 0 & 1 \\-2 & 1 & 0\end{array}\right]\left[\begin{array}{c}\frac{5}{\sqrt{30}} \\\frac{-2}{\sqrt{30}} \\\frac{1}{\sqrt{30}}\end{array}\right]=\left[\begin{array}{c}\frac{1}{\sqrt{5}} \\-\frac{2}{\sqrt{5}}\end{array}\right] u1=σ11Av1=61[1−20110]⎣⎢⎡30530−2301⎦⎥⎤=[51−52]
u 2 = 1 σ 2 A v 2 = 1 1 [ 1 0 1 − 2 1 0 ] [ 0 1 5 2 5 ] = [ 2 5 1 5 ] \boldsymbol{u}_{2}=\frac{1}{\sigma_{2}} \boldsymbol{A} \boldsymbol{v}_{2}=\frac{1}{1}\left[\begin{array}{ccc}1 & 0 & 1 \\-2 & 1 & 0\end{array}\right]\left[\begin{array}{c}0 \\\frac{1}{\sqrt{5}} \\\frac{2}{\sqrt{5}}\end{array}\right]=\left[\begin{array}{c}\frac{2}{\sqrt{5}} \\\frac{1}{\sqrt{5}}\end{array}\right] u2=σ21Av2=11[1−20110]⎣⎡05152⎦⎤=[5251]
U = [ u 1 , u 2 ] = 1 5 [ 1 2 − 2 1 ] \boldsymbol{U}=\left[\boldsymbol{u}_{1}, \boldsymbol{u}_{2}\right]=\frac{1}{\sqrt{5}}\left[\begin{array}{cc}1 & 2 \\-2 & 1\end{array}\right] U=[u1,u2]=51[1−221]
请注意,在计算机上,这样计算的方法的数值性能较差,通常不借助于 A ⊤ A \boldsymbol{A}^{\top} \boldsymbol{A} A⊤A的特征值分解来计算 A \boldsymbol{A} A的奇异值分解。
4.5.3 特征值分解 vs. 奇异值分解
考虑特征分解 A = P D P − 1 \boldsymbol{A}=\boldsymbol{P} \boldsymbol{D} \boldsymbol{P}^{-1} A=PDP−1和奇异值分解 A = U Σ V − 1 \boldsymbol{A}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{-1} A=UΣV−1,下面回顾一下它们的核心内容:
-
对于任意矩阵 R m × n \mathbb{R}^{m \times n} Rm×n,奇异值分解总是存在的。而特征分解仅对平方矩阵 R n × n \mathbb{R}^{n \times n} Rn×n有效,并且仅当我们能找到 R n \mathbb{R}^{n } Rn的特征向量的基时才存在
-
特征分解矩阵 P \boldsymbol{P} P中的向量不一定是正交的,即基的变化不是简单的旋转和缩放。而另一方面,奇异值分解中矩阵 U \boldsymbol{U} U和 V \boldsymbol{V} V中的向量是正交的,因此它们确实表示旋转。
-
特征分解和奇异值分解都是三个线性映射的组合:
– 1. 定义域的基变换
– 2. 每个新基向量的缩放都是独立的并从定义域映射到陪域
– 3. 陪域的基变换
特征分解和奇异值分解的一个关键区别是,在奇异值分解中,定义域和陪域可以是不同维数的向量空间。 -
在奇异值分解中,左奇异向量矩阵 U \boldsymbol{U} U和右奇异向量矩阵 V \boldsymbol{V} V通常不是互逆的(它们在不同的向量空间中执行基变换)。在特征分解中,基变化矩阵 U \boldsymbol{U} U和 U − 1 \boldsymbol{U}^{-1} U−1是互逆的。
-
在奇异值分解中,对角矩阵 Σ \boldsymbol{\Sigma} Σ中的项都是实的、非负的,这对于特征分解中的对角矩阵则不一定成立。
-
奇异值分解和特征分解通过它们的投影关系密切相关
– A \boldsymbol{A} A的左奇异向量是 A A ⊤ \boldsymbol{A}\boldsymbol{A}^{\top} AA⊤的特征向量。
– A \boldsymbol{A} A的右奇异向量是 A ⊤ A \boldsymbol{A}^{\top}\boldsymbol{A} A⊤A的特征向量
– A \boldsymbol{A} A的非零奇异值是 A A ⊤ \boldsymbol{A}\boldsymbol{A}^{\top} AA⊤和 A ⊤ A \boldsymbol{A}^{\top}\boldsymbol{A} A⊤A的非零特征值的平方根。 -
对于对称矩阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n,特征值分解和奇异值分解是相同的,这符合谱定理(定理 4.15)。
值得简要讨论一下SVD的术语和约定,因为有些文献中使用了不同的版本。这些差异对数学分析结果无影响,但这些差异可能令人疑惑。
- 为了便于记法和抽象,我们使用了SVD记法,其中SVD被描述为具有左右两个奇异向量方阵和有一个奇异值非方阵。我们对SVD的这样的定义称为完整SVD(full SVD)
- 一些作者对奇异值分解的定义有点不同,主要集中在奇异值方阵上:对于 A ∈ R m × n , m ≥ n \boldsymbol{A} \in \mathbb{R}^{m \times n},m\ge n A∈Rm×n,m≥n
A m × n = U m × n Σ n × n V n × n ⊤ \underset{m \times n}{\boldsymbol{A}}=\underset{m \times n}{\boldsymbol{U}}\underset{n \times n}{\boldsymbol{\Sigma}} \underset{n \times n}{\boldsymbol{V}}^{\top} m×nA=m×nUn×nΣn×nV⊤
有时这种公式被称为简化SVD(reduced SVD,例如,Datta(2010))或SVD(例如,Press等人(2007))。这种替代格式仅仅改变了矩阵的构造方式,但保持了奇异值分解的数学结构不变。这个替代公式的优点在于 Σ \boldsymbol{\Sigma} Σ是对角矩阵吧,就像在特征值分解中一样。 - 在4.6节中,我们将学习使用奇异值分解的矩阵逼近技术,也称为截断SVD(truncated SVD)。
- 可以定义秩为 r r r的矩阵 A \boldsymbol{A} A的奇异值分解,使得 U \boldsymbol{U} U是 m × r m×r m×r矩阵, Σ \boldsymbol{\Sigma} Σ是 r × r r×r r×r的对角矩阵, V \boldsymbol{V} V是 r × n r×n r×n的矩阵。这种构造与我们的定义非常相似,并确保了对角矩阵 Σ \boldsymbol{\Sigma} Σ只有对角线有非零项。这种替代符号的主要优点是 Σ \boldsymbol{\Sigma} Σ是对角的,就像在特征值分解中一样。
- A \boldsymbol{A} A的奇异值分解只适用于 m > n m\gt n m>n的 m × n m×n m×n矩阵这样限制实际上是不必要的。当 m < n m\lt n m<n时,只会使得SVD分解产生的 Σ \boldsymbol{\Sigma} Σ中零列数目比零行多,即奇异值 σ m + 1 , … , σ n \sigma_{m+1}, \ldots, \sigma_{n} σm+1,…,σn为0。
奇异值分解在机器学习中有着广泛的应用,从曲线拟合中的最小二乘问题到线性方程组的求解。这些应用利用了SVD的各种重要性质和它与矩阵秩的关系以及它能用低秩矩阵逼近给定秩矩阵的能力。用奇异值分解替代一个矩阵通常具有这样的优点:使计算数值的舍入误差(numerical rounding errors)更为稳健。正如我们将在下一节中探讨的那样,SVD以“更简单”的矩阵来近似矩阵的能力扩大了机器学习的应用范围,从降维和主题建模到数据压缩和聚类(dimensionality reduction and topic modeling to data compression and clustering)。
翻译自:
《MATHEMATICS FOR MACHINE LEARNING》作者是 Marc Peter Deisenroth,A Aldo Faisal 和 Cheng Soon Ong
公众号后台回复【m4ml】即可获取这本书。
另外,机器学习的数学基础.pdf