OpenCV图像处理--平面单应性

图像几何变化

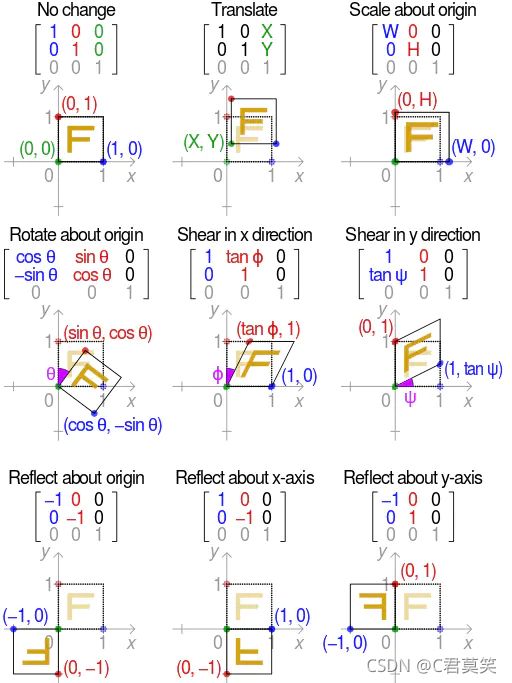
投影变换
投影变换 (Projective Transformation)，是仿射变换的一般化，二者区别如下：

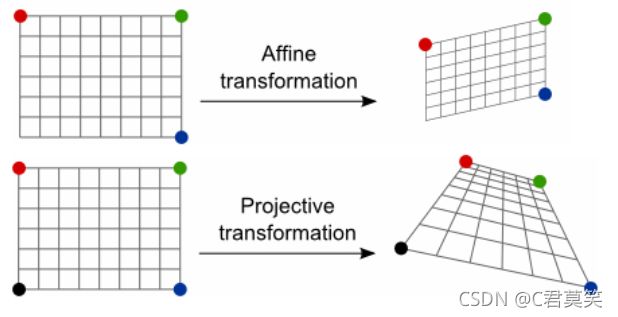
仿射变换

1. 用途
   旋转 (线性变换)，平移(向量加)．缩放(线性变换)，错切，反转

2. 方法
   仿射变换是一种二维坐标到二维坐标之间的线性变换，它保持了二维图形的“平直性”（直线经过变换之后依然是直线）和“平行性”（二维图形之间的相对位置关系保持不变，平行线依然是平行线，且直线上点的位置顺序不变）。任意的仿射变换都能表示为乘以一个矩阵(线性变换)，再加上一个向量 (平移) 的形式．
   

3. 具体应用
   给出变换前的ABCD和变换后的A’B’C’D’
   
   透视变换（投影变换）

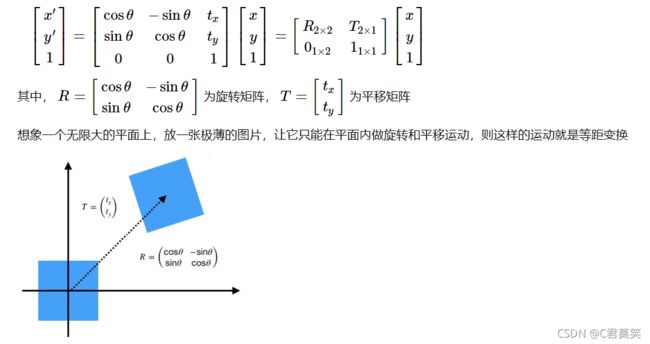
4. 用途
   将2D矩阵图像变换成3D的空间显示效果，全景拼接．

5. 方法
   透视变换是将图片投影到一个新的视平面，也称作投影映射．它是二维（x,y）到三维(X,Y,Z)，再到另一个二维(x’,y’)空间的映射．相对于仿射变换，它提供了更大的灵活性，将一个四边形区域映射到另一个四边形区域（不一定是平行四边形）．它不止是线性变换．但也是通过矩阵乘法实现的，使用的是一个3x3的矩阵，矩阵的前两行与仿射矩阵相同(m11,m12,m13,m21,m22,m23)，也实现了线性变换和平移，第三行用于实现透视变换
   
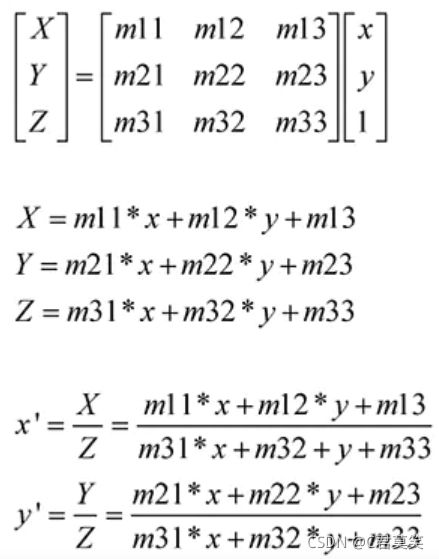
   以上公式设变换之前的点是z值为1的点，它三维平面上的值是x,y,1，在二维平面上的投影是x,y，通过矩阵变换成三维中的点X,Y,Z，再通过除以三维中Ｚ轴的值，转换成二维中的点x’,y’.从以上公式可知，仿射变换是透视变换的一种特殊情况．它把二维转到三维，变换后，再转映射回之前的二维空间（而不是另一个二维空间）．

6. 具体应用
   在OpenCV中，透视变换通过函数cvWrapPerspective(src,dst,mat)实现, 与仿射变换不同的是，透视矩阵是一个3x3的矩阵，在计算矩阵时，可利用函数cvGetPerspectiveTransform(srcQuad,dstQuad,mat)，由于不再是平行四边形，需要提供四边形的四个顶点
   
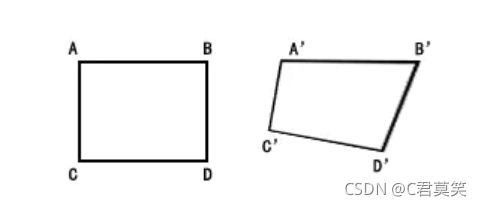
   区别
   仿射变换后平行四边形的各边仍操持平行，透视变换结果允许是梯形等四边形，所以仿射变换是透视变换的子集
   具体案例：
   仿射变换和透视变换的数学原理不需深究，其计算方法为坐标向量和变换矩阵的乘积，换言之就是矩阵运算。在应用层面，仿射变换是图像基于3个固定顶点的变换，如图所示：
   
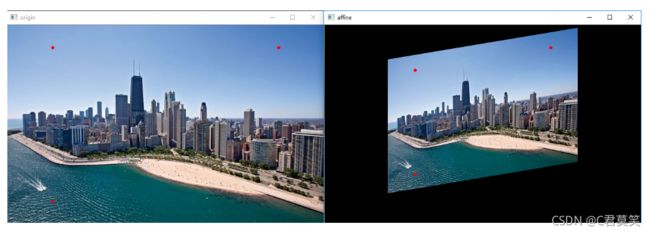
   图中红点即为固定顶点，在变换先后固定顶点的像素值不变，图像整体则根据变换规则进行变换
   同理，透视变换是图像基于4个固定顶点的变换，如图所示：
   
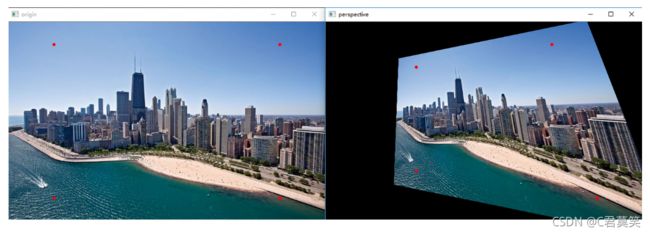
   在OpenCV中，仿射变换和透视变换均有封装好的函数，分别为

void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

与

void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

两种变换函数形式完全相同，因此以仿射变换函数为例：
1、参数InputArray src：输入变换前图像
2、参数OutputArray dst：输出变换后图像，需要初始化一个空矩阵用来保存结果，不用设定矩阵尺寸
3、参数InputArray M：变换矩阵，用另一个函数getAffineTransform()计算
4、参数Size dsize：设置输出图像大小
5、参数int flags=INTER_LINEAR：设置插值方式，默认方式为线性插值
后两个参数不常用，在此不赘述
关于生成变换矩阵InputArray M的函数getAffineTransform()：

Mat getAffineTransform(const Point2f* src, const Point2f* dst)

• 参数const Point2f* src：原图的三个固定顶点

• 参数const Point2f* dst：目标图像的三个固定顶点

• 返回值：Mat型变换矩阵，可直接用于warpAffine()函数

注意，顶点数组长度超过3个，则会自动以前3个为变换顶点；数组可用Point2f[]或Point2f*表示
示例代码如下：

//读取原图
	Mat I = imread("img.jpg");
	//设置空矩阵用于保存目标图像
	Mat dst;
	//设置原图变换顶点
	Point2f AffinePoints0[3] = {
      Point2f(100, 50), Point2f(100, 390), Point2f(600, 50) };
	//设置目标图像变换顶点
	Point2f AffinePoints1[3] = {
      Point2f(200, 100), Point2f(200, 330), Point2f(500, 50) };
	//计算变换矩阵
	Mat Trans = getAffineTransform(AffinePoints0, AffinePoints1);
	//矩阵仿射变换
	warpAffine(I, dst, Trans, Size(I.cols, I.rows));
	//分别显示变换先后图像进行对比
	imshow("src", I);
	imshow("dst", dst);
	waitKey();

同理，透视变换与仿射变换函数类似：

void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())

生成变换矩阵函数为：

Mat getPerspectiveTransform(const Point2f* src, const Point2f* dst)

注意，透视变换顶点为4个

两种变换完整代码及结果比较：

#include 
#include 
using namespace std;
using namespace cv;

Mat AffineTrans(Mat src, Point2f* scrPoints, Point2f* dstPoints)
{
     
	Mat dst;
	Mat Trans = getAffineTransform(scrPoints, dstPoints);
	warpAffine(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);
	return dst;
}

Mat PerspectiveTrans(Mat src, Point2f* scrPoints, Point2f* dstPoints)
{
     
	Mat dst;
	Mat Trans = getPerspectiveTransform(scrPoints, dstPoints);
	warpPerspective(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);
	return dst;
}

void main()
{
     
	Mat I = imread("..//img.jpg");	//700*438

	Point2f AffinePoints0[4] = {
      Point2f(100, 50), Point2f(100, 390), Point2f(600, 50), Point2f(600, 390) };
	Point2f AffinePoints1[4] = {
      Point2f(200, 100), Point2f(200, 330), Point2f(500, 50), Point2f(600, 390) };
	Mat dst_affine = AffineTrans(I, AffinePoints0, AffinePoints1);
	Mat dst_perspective = PerspectiveTrans(I, AffinePoints0, AffinePoints1);

	for (int i = 0; i < 4; i++)
	{
     
		circle(I, AffinePoints0[i], 2, Scalar(0, 0, 255), 2);
		circle(dst_affine, AffinePoints1[i], 2, Scalar(0, 0, 255), 2);
		circle(dst_perspective, AffinePoints1[i], 2, Scalar(0, 0, 255), 2);
	}

	imshow("origin", I);
	imshow("affine", dst_affine);
	imshow("perspective", dst_perspective);
	waitKey();
}

结果如图：

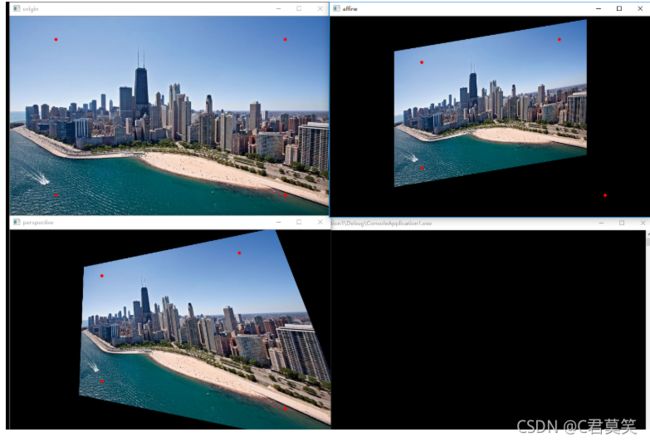
可以看出，仿射变换以3个点为基准点，即使数组长度为4也仅取前3个点作为基准点；透视变换以4个点为基准点，两种变换结果不相同。应根据实际情况判断使用哪种变换方式更佳