R语言学习笔记7_方差分析
目录
- 七、方差分析
-
- 7.1 单因子方差分析
-
- 7.1.1 数学模型
-
- 方差分析表
- 7.1.2 均值的多重比较
-
- 多重 t 检验方法
-
- ==差异显著与显著差异的区分==
- ==置信区间的易混淆==
- 7.1.3 同时置信区间:Tukey法
- 7.1.4 方差齐性检验
-
- Barlett检验
- Levene检验
- 注意
- 7.2 双因子方差分析
-
- 7.2.1 无交互作用的方差分析
- 7.2.2 有交互作用的方差分析
- 7.3 协方差分析
七、方差分析
方差分析的主要工作就是将观测数据的总变异按照变异原因的不同分解为因子效应与试验误差,并对其做出数量分析,比较各种原因在总变异中所占的重要程度,以此作为进一步统计推断的依据。
前提条件:独立、正态、方差齐性
7.1 单因子方差分析
7.1.1 数学模型
设试验仅有一个因子(因素)A,其有r个水平A1,A2,…,Ar,现在水平Ai下进行ni次独立观测,得到观测数据Xij,j=1,2,…,ni,i=1,2,…,r
SST 总离差平方和(总变差):Xij与总平均值之差的平方和,描绘所有数据的离散程度。
SSE 误差平方和(组内平方和):对固定的水平i,观测值Xij之间的差异大小的度量。
SSA 因素A的效应平方和(组间平方和):因子A各水平下的样本均值和总平均值的平方和。
aov(formula, data = NULL, projections = FALSE, qr = TRUE, contrasts = NULL, ...)
formula 是方差分析的公式,在单因素方差分析中表示为 x~A, data 是数据框。
例: 对除杂方法进行选择。在实验中选用5种不同的除杂方法,每种方法做4次试验,即重复4次,如下表所示。
除杂方法Ai 除杂量Xij 平均量 A1 25.6 22.2 28.0 29.8 26.4 A2 24.4 30.0 29.0 27.5 27.7 A3 25.0 27.7 23.0 32.2 27.0 A4 28.8 28.0 31.5 25.9 28.6 A5 20.6 21.2 22.0 21.2 21.3
> x<- c(25.6, 22.2, 28.0, 29.8,24.4 ,30.0 ,29.0, 27.5,25.0 ,27.7, 23.0 ,32.2,28.8, 28.0, 31.5 ,25.9,20.6, 21.2, 22.0 ,21.2)
> A<-factor(rep(1:5,each=4))
> miscellany<-data.frame(x,A)
> aov.mis<-aov(x~A,data=miscellany)
> summary(aov.mis)
Df Sum Sq Mean Sq F value Pr(>F)
A 4 132 33.0 4.31 0.016 *
Residuals 15 115 7.7
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Df 表示自由度,Sum Sq 表示平方和,Mean Sq表示均方和,F value 表示F检验统计量的值,Pr(>F)表示检验p的值, A 就是因素, Residuals 为残差。
可以看出F=4.31>F0.05(5-1,20-5)=3.06,或p=0.0016<0.05说明有理由拒绝原假设,即认为五种除杂方法的差异显著。
方差分析表
据上述结果可以填写下面的方差分析表:
| 方差来源 | 自由度df | 平方和SS | 均方和MS | F比 | p值 |
|---|---|---|---|---|---|
| 因素A | 4 | 132 | 33.0 | 4.31 | 0.016 |
| 残差E | 15 | 115 | 7.7 | ||
| 总和T | 19 | 247 |
> plot(miscellany$x~miscellany$A)
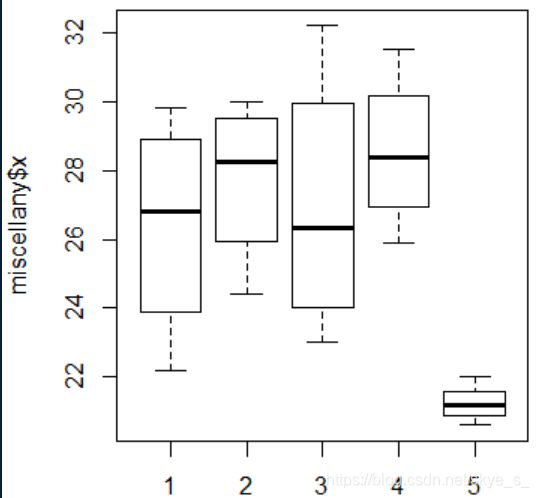
从上图也可以看出5种除杂方法产生的除杂量有显著差异,特别是第5种与前4种,而方法1和3,方法2和4的差异不明显。
7.1.2 均值的多重比较
之前在进行方差分析后发现各效应的均值之间有显著差异,只能知道有某些均值彼此不同,但不知道具体是哪些均值不同。
多重 t 检验方法
当多次重复使用该方法时,会增大犯第一类错误的概率,从而使得结论不一定可靠。所以在进行较多次重复比较时,要对p值进行调整:
p.adjust(p, method = p.adjust.methods, n = length(p))
p是p值构成的向量,method是修正方法。
当比较次数较多时,Bonferroni方法的效果较好。
得到多重比较的p值:
pairwise.t.test(x, g, p.adjust.method = p.adjust.methods, pool.sd = !paired, paired = FALSE, alternative = c("two.sided", "less", "greater"), ...)
x是响应变量构成的向量,g是分组向量(因子), p.adjust.methods是上面提到的调整p值的方法,p.adjust.methods=none表示不做任何调整。默认值按Holm方法进行调整。
例:对上例作均值的多重比较,进一步检验。
下面用三种方法进行多重比较:
1)不对p作出调整
> pairwise.t.test(x,A,p.adjust.method = 'none')
Pairwise comparisons using t tests with pooled SD
data: x and A
1 2 3 4
2 0.509 - - -
3 0.773 0.707 - -
4 0.289 0.679 0.434 -
5 0.019 0.005 0.010 0.002
P value adjustment method: none
2)按默认值”holm“对p值进行调整
> pairwise.t.test(x,A)
Pairwise comparisons using t tests with pooled SD
data: x and A
1 2 3 4
2 1.00 - - -
3 1.00 1.00 - -
4 1.00 1.00 1.00 -
5 0.13 0.04 0.08 0.02
P value adjustment method: holm
3)按”bonferroni“对p值进行调整
> pairwise.t.test(x,A,p.adjust.method = "bonferroni")
Pairwise comparisons using t tests with pooled SD
data: x and A
1 2 3 4
2 1.00 - - -
3 1.00 1.00 - -
4 1.00 1.00 1.00 -
5 0.19 0.05 0.10 0.02
P value adjustment method: bonferroni
从输出结果可以看出,做调整后p值增大,在一定程度上克服了多重t检验的缺点。
差异显著与显著差异的区分
由于常用“显著”来表示P值大小,所以P值最常见的误用是把统计学上的显著与临床或实际中的显著差异相混淆,即混淆“差异具有显著性”和“具有显著差异”二者的意思。其实,前者指的是p<=0.05,即说明有充分的理由认为比较的二者来自同一总体的可能性不足5%,因而认为二者确实有差异,下这个结论出错的可能性<=5%。而后者的意思是二者的差别确实很大。举例来说,4和40的差别很大,因而可以说是“有显著差异”,而4和4.2差别不大,但如果计算得到的P值<=0.05,则认为二者“差别有显著性”,但是不能说“有显著差异”。
————————————————
原文链接:https://blog.csdn.net/yu1581274988/article/details/117295802置信区间的易混淆
参数95%的置信度在区间A的意思是:
正确:采样100次计算95%置信度的置信区间,有95次计算所得的区间包含真实值。
错误:采样100次,有95次真实值落在置信区间。
真实值不会变,变的是置信区间。
————————————————
原文链接:https://blog.csdn.net/yimingsilence/article/details/78084810
7.1.3 同时置信区间:Tukey法
对效应之差αi-αj做出置信区间,由此了解哪些效应不相等。
TukeyHSD(x, which, ordered = FALSE, conf.level = 0.95, ...)
x是方差分析的对象, which是给出需要计算比较区间的因子向量, ordered为T则因子的水平递增排序,从而使得因子间差异均以正值出现。
例:某商店以各自的销售方式卖出新型手表,连续四天手表的销量如下表所示。试考察销售方式之间是否有显著差异?
销售方式 销售量数据 A1 23 19 21 13 A2 24 25 28 27 A3 20 18 19 15 A4 22 25 26 23 A5 24 23 26 27
#生成数据
> sales<-data.frame(x=c(23, 19, 21, 13,24 ,25, 28, 27,20 ,18 ,19 ,15,22, 25 ,26 ,23,24 ,23 ,26, 27),A=factor(rep(1:5,c(4,4,4,4,4))))
#进行方差分析
> summary(aov(x~A,sales))
Df Sum Sq Mean Sq F value Pr(>F)
A 4 213 53.2 7.98 0.0012 **
Residuals 15 100 6.7
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#可见,不同销售方式有差异,求均值之差的同时置信区间
> TukeyHSD(aov(x~A,sales))
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = x ~ A, data = sales)
$A
diff lwr upr p adj
2-1 7 1.3622 12.638 0.0120
3-1 -1 -6.6378 4.638 0.9806
4-1 5 -0.6378 10.638 0.0945
5-1 6 0.3622 11.638 0.0344
3-2 -8 -13.6378 -2.362 0.0042
4-2 -2 -7.6378 3.638 0.8062
5-2 -1 -6.6378 4.638 0.9806
4-3 6 0.3622 11.638 0.0344
5-3 7 1.3622 12.638 0.0120
5-4 1 -4.6378 6.638 0.9806
7.1.4 方差齐性检验
检验数据在不同水平下方差是否相同。
Barlett检验
H0:各因子水平下的方差相同,H1:各因子水平下的方差不齐。
bartlett.test(x, g, ...)
bartlett.test(formula, data, subset, na.action, ...)
x是由数据构成的向量或列表,g是由因子构成的向量(当x是列表时,此项无效);
formula是方差分析公式,data是数据框。
Levene检验
levene.test(x,group)
leveneTest(y, group, center=median, ...)
x是数据构成的向量,g是由因子构成的向量。
例:对上例数据作方差齐性检验。
1)用 Barlett检验
> bartlett.test(x~A,data=sales)
Bartlett test of homogeneity of variances
data: x by A
Bartlett's K-squared = 3.7, df = 4, p-value = 0.4
由于p=0.4>0.05,故接受原假设,认为各处理组数据是等方差的。
2)用 Levene检验
> leveneTest(sales$x,sales$A)
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 4 0.82 0.53
15
注意
- 方差分析模型可视为一种特殊的线性模型,因此可以使用线性模型函数
lm(),并用函数anova()提取其中的方差分析表。因此aov(formula)等价于anova(lm(formula))。 - 单因子方差分析还可以使用函数
oneway.test(),若各水平下数据的方差相等(var.equal=TRUE),等同于使用函数aov()进行一般的方差分析;若各水平下数据的方差不相等(var.equal=FALSE)则使用Welch(1951)的近似方法进行方差分析。 - 当各水平下的分布未知时,则采用Kruskal-Wallis秩和检验进行方差分析。
7.2 双因子方差分析
7.2.1 无交互作用的方差分析
仍可以用函数aov(),方差模型公式为x~A+B,加号表示两个因素具有可加性。
例:原来检验果汁中含铅量有三种方法A1,A2,A3,现研究出另一种快速检验法A4,能否用A4替代前三种方法,需要通过试验考察。观察的对象是果汁,不同的果汁当作不同的水平:B1为苹果,B2为葡萄汁,B3为西红柿汁,B4为苹果汁,B5为橘子汁,B6为菠萝柠檬汁。现进行双因素交错搭配试验,即用四种方法同时检验每一种果汁,其检验结果如下表所示。问因素A(检验方法)和B(果汁品众)对果汁的含铅量是否有显著影响?
A B1 B2 B3 B4 B5 B6 xi· A1 0.05 0.46 0.12 0.16 0.84 1.30 2.93 A2 0.08 0.38 0.40 0.10 0.92 1.57 3.45 A3 0.11 0.43 0.05 0.10 0.94 1.10 2.73 A4 0.11 0.44 0.08 0.03 0.93 1.15 2.74 x·j 0.35 1.71 0.65 0.39 3.63 5.12 X··=11.85
> juice<-data.frame(x=c(0.05,0.46,0.12,0.16,0.84,1.30,0.08,0.38,0.40,0.10,0.92,1.57,0.11,0.43,0.05,0.10,0.94,1.10,0.11,0.44,0.08,0.03,0.93,1.15),A=gl(4,6),B=gl(6,1,24))
> #gl(n,k,length=n*k,labels=1:n,ordered=FALSE) n是水平数,k是每一水平上的重复次数,length是总观测值数,ordered指明各水平是否先排序。
> juice.aov<-aov(x~A+B,data=juice)
> summary(juice.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 3 0.06 0.019 1.63 0.22
B 5 4.90 0.980 83.98 2e-10 ***
Residuals 15 0.18 0.012
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> #p说明B对含铅量有显著影响,而没有充分理由说明A对铅含量有显著影响。
> bartlett.test(x~A,data=juice)
Bartlett test of homogeneity of variances
data: x by A
Bartlett's K-squared = 0.27, df = 3, p-value = 1
> bartlett.test(x~B,data=juice)
Bartlett test of homogeneity of variances
data: x by B
Bartlett's K-squared = 17, df = 5, p-value = 0.004
> #因素B不满足方差齐性要求。
7.2.2 有交互作用的方差分析
仍可以用函数aov(),方差模型公式为x~A+B+A:B或x~A*B
例:有一个关于检验毒品强弱的试验,给48只老鼠注射三种毒药(因素A),同时有4种治疗方案(因素B),这样的试验在每一种因素组合下都重复四次测试老鼠的存活时间,数据如下表所示。试分析毒药和治疗方案以及它们的交互作用对老鼠存活时间有无显著影响?
A B C D 1 0.31 0.45 0.46 0.43 0.82 1.10 0.88 0.72 0.43 0.45 0.63 0.76 0.45 0.71 0.66 0.62 2 0.36 0.29 0.40 0.23 0.92 0.61 0.49 1.24 0.44 0.35 0.31 0.40 0.56 1.02 0.71 0.38 3 0.22 0.21 0.18 0.23 0.30 0.37 0.38 0.29 0.23 0.25 0.24 0.22 0.30 0.36 0.31 0.33
#建立数据框
> rats<-data.frame(x=c(0.31 ,0.45, 0.46 ,0.43,0.82 ,1.10, 0.88, 0.72,0.43, 0.45, 0.63, 0.76,0.45, 0.71 ,0.66 ,0.62,0.36, 0.29 ,0.40 ,0.23,0.92, 0.61, 0.49 ,1.24,0.44 ,0.35, 0.31, 0.40,0.56, 1.02, 0.71, 0.38,0.22 ,0.21 ,0.18 ,0.23,0.30, 0.37 ,0.38, 0.29,0.23 ,0.25, 0.24 ,0.22,0.30 ,0.36, 0.31, 0.33),A=gl(3,16,48,labels = c("1","2","3")),B=gl(4,4,48,labels = c("A","B","C","D")))
> par(mfrow=c(1,2)) #修改图的布局
> plot(x~A+B,data=rats) #显示各因素水平均有较大差异
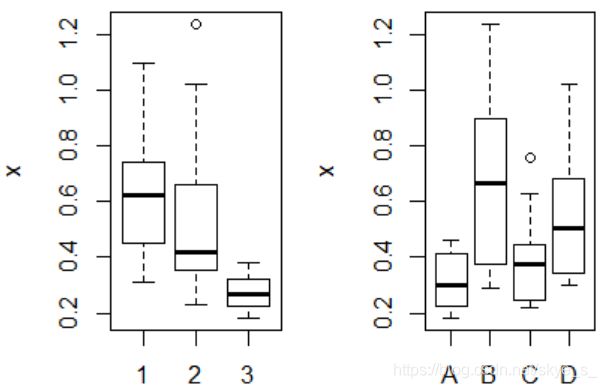
用函数interaction.plot()作出交互效应图,以考查因素之间交互作用是否存在。
> with(rats,interaction.plot(A,B,x,trace.label = "B"))
> with(rats,interaction.plot(B,A,x,trace.label = "A"))
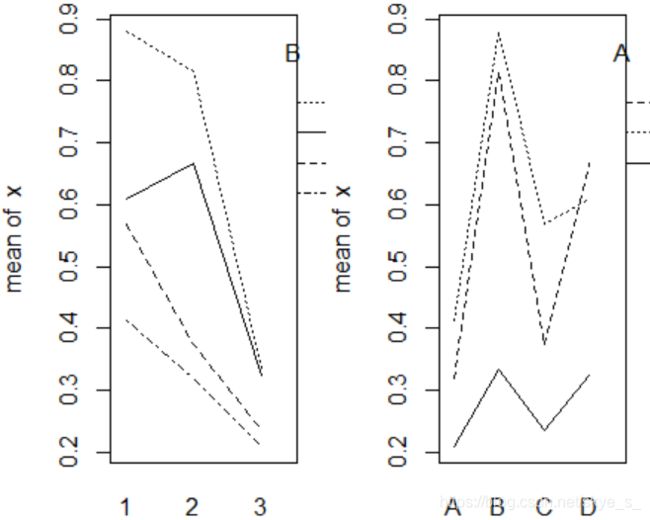
两图中的曲线并没有明显相交的情况出现,因此初步认为两个因素没有交互作用。进一步用aov()函数检验。
> rats.aov<-aov(x~A*B,data = rats)
> summary(rats.aov)
Df Sum Sq Mean Sq F value Pr(>F)
A 2 1.033 0.517 23.22 3.3e-07 ***
B 3 0.921 0.307 13.81 3.8e-06 ***
A:B 6 0.250 0.042 1.87 0.11
Residuals 36 0.801 0.022
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
发现毒药、治疗方案对老鼠的治疗时间有显著影响,而交互作用的影响不显著。
最后检验因素A、B下的数据是否满足方差齐性的要求:
> bartlett.test(rats$x,rats$A)
Bartlett test of homogeneity of variances
data: rats$x and rats$A
Bartlett's K-squared = 26, df = 2, p-value = 2e-06
> bartlett.test(rats$x,rats$B)
Bartlett test of homogeneity of variances
data: rats$x and rats$B
Bartlett's K-squared = 13, df = 3, p-value = 0.004
发现p值均小于0.05,不满足要求,这与一开始的箱线图是一致的。
7.3 协方差分析
协方差分析ANCOVA:是将线性回归分析与方差分析结合起来的一种统计方法。基本思想是:将一些对响应变量Y有影响的变量(指未知或难以控制的因素)看作协变量,建立响应变量Y随协变量X变化的线性回归关系,并利用这种回归关系把X值化为相等后再对各处理组Y的修正均值间的差别进行假设检验。其实质就是从Y的总平方和中扣除X对Y的回归平方和,对残差平方和作进一步分解后,再进行方差分析,以更好地评价这种处理的效应。
在比较两组或多组均数间差别的同时扣除或均衡这些不可控因素的影响
ancova(formula, data.in = NULL, ...,
x, groups, transpose = FALSE,
display.plot.command = FALSE,
superpose.level.name = "superpose",
ignore.groups = FALSE, ignore.groups.name = "ignore.groups",
blocks, blocks.pch = letters[seq(levels(blocks))],
layout, between, main,
pch=trellis.par.get()$superpose.symbol$pch)
formula是协方差分析的公式,data.in是数据框,x是协方差分析中的协变量,在作图时若formula中没有x则需要指出,groups是因子。
例:为研究A,B,C,三种饲料对猪的催肥效果,用每种饲料喂养8头猪一段时间,测得每头猪的初始重量X和增重Y。试分析三种饲料对猪的催肥效果是否相同?
A B C X1 Y1 X2 Y2 X3 Y3 1 15 85 17 97 22 89 2 13 83 16 90 24 91 3 11 65 18 100 20 83 4 12 76 18 95 23 95 5 12 80 21 103 25 100 6 16 91 22 106 27 102 7 14 84 19 99 30 105 8 17 90 18 94 32 110
饲料是认为可以控制的定性因素;猪的初始重量是难以控制的定量因子,为协变量X;实验的观察指标是猪的增量,为响应变量Y;各组的增重由于受猪的原始体重影响,不能直接进行方差分析,需进行协方差分析。
#建立数据集
> feed<-rep(c('A','B','C'),each=8)
> X<-c(15,13,11,12,12,16,14,17,17,16,18,18,21,22,19,18,22,24,20,23,25,27,30,32)
> Y<-c(85,83,65,76,80,91,84,90,97,90,100,95,103,106,99,94,89,91,83,95,100,102,105,110)
> pig<-data.frame(feed,X,Y)
1)认为在三种不同饲料喂养下,猪的初试体重不同,但增长速度相同
> ancova(Y~X+feed,data=pig)
Analysis of Variance Table
Response: Y
Df Sum Sq Mean Sq F value Pr(>F)
X 1 1621 1621 142.4 1.5e-10 ***
feed 2 707 354 31.1 7.3e-07 ***
Residuals 20 228 11
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

可见猪的初始体重和增长速度对猪的增重都有显著差异。
2)认为在三种不同饲料喂养下,猪的初始体重和增长速度都不同
> ancova(Y~X*feed,data=pig)
Analysis of Variance Table
Response: Y
Df Sum Sq Mean Sq F value Pr(>F)
X 1 1621 1621 162.49 1.9e-10 ***
feed 2 707 354 35.44 5.7e-07 ***
X:feed 2 48 24 2.41 0.12
Residuals 18 180 10
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
