【算法】用习题教你如何使用动态规划，超详细，一看就会！！建议收藏！！

只要能坚持看完，我相信你一定能学到！！

---

前言

动态规划（DP）的定义：动态规划是分治思想的延伸，通俗一点来说就是大事化小，小事化无的艺术。
动态规划具备了以下三个特点：

1. 把原来的问题分解成了几个相似的子问题。
2. 所有的子问题都只需要解决一次。
3. 储存子问题的解

并且我们通常从以下的四个角度来出发（重要）

1. 状态定义
2. 状态间的转移方程定义
3. 状态的初始化
4. 返回结果

一、为何要使用动态规划？

我们首先看这样一道题目

斐波那契

点击链接跳转：斐波那契数列

同学们可能在初始学习C语言，学到递归的时候肯定少不了 这道经典的题目,大家通常也都是用递归的方式去完成，但是我们发现一点，当我们用递归实现斐波那契数的算法是2^n的时间复杂度，数字给的大的时候就求不出来了，这时我们就会用到动态规划的思想
废话不多说，现在我们来看看按照我们上面给的逻辑如何用我们的四个步骤完成这道题目

状态的定义：求F(n)的值
状态方程的转换：F(n)=F(n-1)+F(n-2)
初始化： F（0） =0；F(1)=1
返回结果：F（n）

C++实现：
class Solution {
     
public:
    int Fibonacci(int n) {
     
        vector<int> v;
        //初始化
        v.push_back(0);
        v.push_back(1);
        //状态的转移方程
        for(int i=2;i<=n;i++)
        {
     
           int ret  = v[i - 1] + v[i - 2];
            v.push_back(ret);
        }
        //返回结果
        
        return v[n];
    }
};

---

二、最大连续的子数组和

最大连续的子数组和

int FindGreatestSumOfSubArray(vector<int> array) 

这里我们就该思考他的状态如何定义，假设我们这里用前i个元素的数组的最大和作为状态的定义，我们会发现，我们无法利用前一个状态，做出变化转换到下一个状态。
我们这里的状态定义：以第i个元素为结尾的最大的子数组和
原因：我们在新增元素进去时，我们就可以根据新增元素是否需要加入进去并且保持是一个连续的子数组和
状态递推：F[i] = max(F[i-1]+array[i-1],array[i-1]);意思即上一个最大值是否加入当前值与该元素本身比较后将大的放入F（i）中
结果：返回我们数组当中最大的值即是在这个数组当中的最大的子数组和

class Solution {
     
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
     
        int sz = array.size();
        vector<int> F(sz+1);
        //初始化
        F[1] = array[0];
        for(int i =2;i<=sz;i++)
        {
     
            //递推方程：以i结尾的子数组最大和
            F[i] = max(F[i-1]+array[i-1],array[i-1]);
        }
        int maxI = F[1];
        for(int i =2 ;i<= sz;++i)
        {
     
            maxI = max(F[i],maxI);
        }
        return maxI;
    }
};

---

三、LC12 拆分词句

LC12 拆分词句

bool wordBreak(string s, unordered_set<string> &dict) 

分析题意：就是要我们在给定的字符串中判断是否能将字符串分割成字典dict中能找到的值
状态定义： 前i个字符能否在dict中查找到
**状态转换：**这里先解释一点，状态的转换不一定是一个等式，比如在这个地方，定义为，j 为dict中单词，解释一下，就是我们要利用前面j个字符的状态，当前面的j个字符为在dict中能中能找到，即F（j）为真，我们只需要在判断(j+1，i)这个区间也是在dict当中能查找的字串就能保证整体为真了！（这里的F(j)是两个或多个字符组成的都没关系，在dict当中能找到就表明他是真）
初始化：我们这里的起始状态可以给一个"",表示空串，在这个的基础上的状态转换方程表示的是，字符串整体能在dict中查找到，即将F[0] 置成ture

class Solution {
     
public:
    bool wordBreak(string s, unordered_set<string> &dict) {
     
// 前j个字符能在dict中查找
// 状态方程：j
// 特殊情况：第一个字符
// F[0] ture, F[1] --要把F[0]弄成辅助状态，这样表示前j个字符为整体的时候在dict中能查找
        int n = s.size();
        vector<bool> canBreak(n+1 ,false);//前i个字符 -- 映射下标位置
        canBreak[0]=true;//这个是辅助状态
        for(int i= 1; i <= n;i++)//处理第一个到第n个字符
        {
     
            for(int j =i-1 ; j >= 0 ;j--)
            {
     
               if(canBreak[j] && dict.find(s.substr(j,i-j))!=dict.end())// 状态方程：j
               {
     
                   canBreak[i] =true;
               }
            }
        }
        return canBreak[n];
    }
};

这题的状态转换其实就没有之前的两道题好想了，但是我们在思考的时候能够想到状态的转换问题其实就已经解决了，所以很多时候都是只差临门一脚

---

四、三角形

跳转链接：三角形

int minimumTotal(vector<vector<int> > &triangle) 

像题目所给的这种我们很容易就能判断出来结果，但如果我们将第三行的70改成1的话我们答案会如何呢


下图演示的例子：
初始化的例子：

分析：观察上图的两张表，我们可以看出，要求出从上到下的最小和，并且一次移动只能移动到从(i,j)–> (i+1,j),(i+1,j+1) ，很明显我们不能就直接选择下一行的最小值，所以我们要个二维数组去保存所有的子数组的和F(i,j)
状态定义：到第i行的最小值
状态转换：以图中的50分析：因为当前行的大小是由 F(i,j) -->
min(F(i-1,j),F(i-1,j-1))+(i,j)，即我们可以保存从上面下来的所有情况的最小和，例如：50这个位置就是从20 -->30–>50，所以50对应的二维数组存放这100-- 这样说应该就能理解了
初始化：可以从上面的图看出，当 j== 0时，即第一列和当 i==j时，对角线他们的可能只能是从固定位置下来的，所以我们初始化的时候先将这些值置成对应的值
解题：我的解题当中所用的是直接在他们给我们的二维数组triangle中更新，因为我们遍历数组的时候刚好可以就将值更新好放回去

class Solution {
     
public:
    int minimumTotal(vector<vector<int> > &triangle) {
     
//         直接用triangle二维数组记录当前位置的最小值

// 初始化第0列的应该加上上一行的值加上这一行的值。i==j的就可以上一(i-1,j-1)的值加上当前值，其他的位置就可以是上一行的和上一行上一列的最小值加上当前值
        int x =triangle.size();
        for(int i =1;i<x;i++)
        {
     
            for(int j=0;j<i+1;j++)
            {
     
                if(j==0)
                    triangle[i][j]=triangle[i-1][j]+triangle[i][j];
                else if(i == j)
                {
     
                    triangle[i][j]=triangle[i-1][j-1]+triangle[i][j];
                }
                else
                {
     
                    triangle[i][j]=triangle[i][j]+min(triangle[i-1][j-1],triangle[i-1][j]);
                }
            }
        }
        int y =triangle[x-1].size();
        int minret= triangle[x-1][0];
        for(int i=1;i<y;++i)
        {
     
            minret = min(minret,triangle[x-1][i]);
        }
        return minret;
    }
};

---

五、LC88 求路径

LC88 求路径

解析：这道题的题意非常简单，从起点到终点求路径，且每次只能往下或者往右

根据上图：其实每个点路径和是上一行和左一列到该位置的路径和相加，所以我们用一个二维数组去保存子答案的结果
状态定义: 从(0,0)到（i，j）的路径数
状态转换：F(i,j) =F(i-1,j)+F(i,j-1) – 即每个点的路径和个数为上一行和左边一列的和相加
初始化：观察到第一行和第一列，他们都只有一种可能性，一直往右走，和一直往下走，所以初始化的时候我们将他们全部置成1；
返回：F（m-1，n-1）

class Solution {
     
public:
    /**
     * 
     * @param m int整型 
     * @param n int整型 
     * @return int整型
     */
    int uniquePaths(int m, int n) {
     
        // write code here
        //状态转换 --(i,j)是(i-1,j)与(i,j-1)走多一步得到的
        vector<vector<int>> retArr(m,vector<int>(n,0));
        retArr[0][0]=1;
        for(int i =1;i<m;++i)
        {
     
            
            retArr[i][0]=1;//处理第一列
        }
        for(int i =1;i<n;++i)
        {
     
            retArr[0][i]=1;//处理第一行
        }
        for(int i = 1;i<m;++i)
        {
     
            for(int j =1;j<n;++j)
            {
     
                retArr[i][j] =retArr[i-1][j]+retArr[i][j-1];
            }
        }
        return retArr[m-1][n-1];
    }
};

---

六、LC87 求路径 ii

LC87 求路径 ii

分析：比起上一题这里就是添加了障碍，在有障碍的地方我们置成路径和为0的话，那么结论每个点路径和是上一行和左一列到该位置的路径和相加，所以我们用一个二维数组去保存子答案的结果在这里也是适用的

状态定义: 从(0,0)到（i，j）的路径数
状态转换：F(i,j) =F(i-1,j)+F(i,j-1) – 即每个点的路径和个数为上一行和左边一列的和相加
初始化：初始化我们将第一行，第一列有路障的后面置0，并且(0,0)如果是有路障或者终点处有路障直接就返回0
技巧： 我们可以将我们的二维数组提前置成0，这样初始化遍历的时候我们break跳出循环相当于也将后面的初始化完成了，具体看下面的代码吧！！！

class Solution {
     
public:
    /**
     * 
     * @param obstacleGrid int整型vector> 
     * @return int整型
     */
    int uniquePathsWithObstacles(vector<vector<int> >& obstacleGrid) {
     
        // write code here
//         到(i,j)！=1的时候就有
// 也等于（i-1,j） 和（i,j-1）
// 初始化的时候0,0 为1直接返回
// 初始化之后我们将有障碍的都置成0，这样我们就可以套用上题的思路
        if(obstacleGrid.empty())
            return 0;
        int x =obstacleGrid.size();
        int y =obstacleGrid[0].size();
        if(obstacleGrid[0][0]||obstacleGrid[x-1][y-1])
            return 0;
        vector<vector<int>> retArr(x,vector<int>(y,0));//置成0方便后续我们操作
        for(int i=0;i<x;i++)
        {
     
            if(obstacleGrid[i][0] == 1)
                break;//有障碍的话我们就直接退出
            retArr[i][0]=1;
        }
        for(int i=0;i<y;i++)
        {
     
            if(obstacleGrid[0][i] == 1)
                break;
            retArr[0][i]=1;
        }
        for(int i =1;i<x;i++)
        {
     
            for(int j =1;j<y;j++)
            {
     
                if(obstacleGrid[i][j]==0)
                retArr[i][j] = retArr[i-1][j]+retArr[i][j-1];
                else
                retArr[i][j]= 0;
            }
        }
        return retArr[x-1][y-1];
    }
};

相似的题目：LC86 带权值的最小路径和，自己也动手试试吧

---

七、 背包问题

背包问题

如果看到这题的时候，你已经在能够自己推导这道题的状态定义和转换方程，再来听听我讲的，那么这道题可能会比较容易吸收

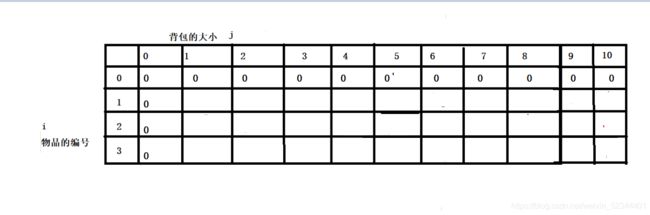
状态：
F(i, j): 前i个物品放入大小为j的背包中所获得的最大价值，如果不将j置成变量的话前i个物品放入背包中所获得的最大价值，是没有办法判断当前背包大小是否够放当前物品的 – 难
状态递推：对于第i个商品，有一种例外，装不下，两种选择，放或者不放
如果装不下：此时的价值与前i-1个的价值是一样的
F(i,j) = F(i-1,j)，如果可以装入：需要在两种选择中找最大的
F(i, j) =max(F[i-1][j-A[i-1]]+V[i-1],F[i-1][j])
F(i-1,j): 表示不把第i个物品放入背包中， 所以它的价值就是前i-1个物品放入大小为j的背包的最大价值
F(i-1, j - A[i]) + V[i]：表示把第i个物品放入背包中，价值在该物品价值的基础上增加V[i],但是需要腾出j - A[i]的大小放第i个商品

我们以题目的情况进行分析
初始化：

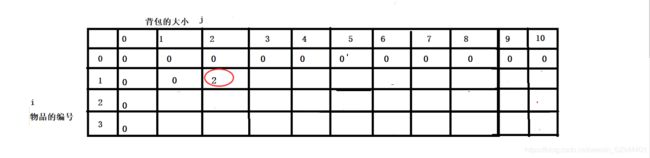
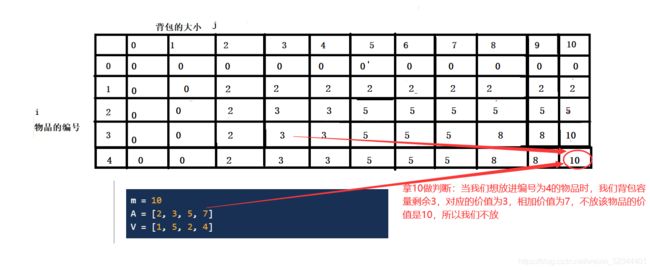
这里对2这个点单独分析一下，后面的也跟这个类似，当我们考虑是否要放2的时候，我们要考虑放完之后的剩余容量j-A[i-1] ，这里值为0，所以我们加上上一行背包大小为0时的值，即当前的最大值
max(vv[i-1][j-A[i-1]]+V[i-1],vv[i-1][j])
下面再给一个例子

---

总结

动态规划的题要自己多做做，这些题都得做做，做的多了自然就会有思路了。下次我们讲讲回文串分割，编辑问题和不同的子序列，这节的知识如果没看懂的欢迎来与我讨论，制作不易，一键三连！！