TensorFlow 从入门到精通（-2）—— Keras概述

这是一条新的通道，记录我神经网络的课程笔记和课件，序号从-2开始。

TensorFlow2教程-Keras概述

Keras 是一个用于构建和训练深度学习模型的高阶 API。它可用于快速设计原型、高级研究和生产。

Keras的3个优点：
方便用户使用、模块化和可组合、易于扩展

1 导入tf.keras

TensorFlow2推荐使用tf.keras构建网络，常见的神经网络都包含在tf.keras.layer中(最新的tf.keras的版本可能和keras不同)

import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras.callbacks import EarlyStopping, TensorBoard
import numpy as np
from datetime import datetime

gpu_ok = tf.test.is_gpu_available()

print(tf.__version__)
print(tf.keras.__version__)
print(gpu_ok)

2.1.0
2.2.4-tf
True

2 构建简单模型

2.1 模型堆叠

最常见的模型类型是层的堆叠：tf.keras.Sequential 模型
搭建完网络后，可以通过summary函数查看网络模型。
使用summary函数有三个前提

1，需要指定输入层维数

2，或调用build（）

3，或调用fit（）

其中，2、3需要有训练集
总之，要知道输入层的维数

model = tf.keras.Sequential()
model.add(layers.Dense(32, activation='relu', input_dim=72))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
model.summary()

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 32)                2336      
_________________________________________________________________
dense_1 (Dense)              (None, 32)                1056      
_________________________________________________________________
dense_2 (Dense)              (None, 10)                330       
=================================================================
Total params: 3,722
Trainable params: 3,722
Non-trainable params: 0
_________________________________________________________________

2.2 网络配置

tf.keras.layers中主要的网络配置参数如下：
activation：设置层的激活函数。此参数可以是函数名称字符串，也可以是函数对象。默认情况下，系统不会应用任何激活函数。
kernel_initializer 和 bias_initializer：创建层权重（核和偏置）的初始化方案。此参数是一个名称或可调用的函数对象，默认为 “Glorot uniform” 初始化器。
kernel_regularizer 和 bias_regularizer：应用层权重（核和偏置）的正则化方案，例如 L1 或 L2 正则化。默认情况下，系统不会应用正则化函数。
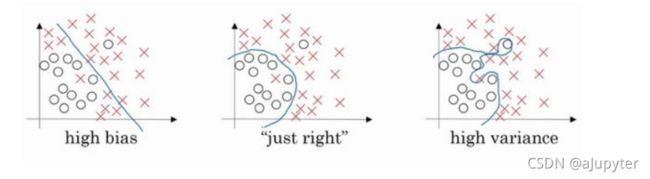
正则化的目的是为了解决过拟合（overfitting）问题

公式——略过

左边的分类会有很大误差，而右边的分类方式就是过拟合，泛化能力很差。中间图虽有误差，但是的确是最佳方案

现在我们来看下这个庞大的深度拟合神经网络。我知道这张图不够大，深度也不够，但你可以想象这是一个过拟合的神经网络。我们添加正则项，它可以避免数据权值矩阵过大，但为什么这样可以减少过拟合？

直观上理解就是如果正则化设置得足够大，权重矩阵被设置为接近于0的值，即把多隐藏单元的权重设为0，于是基本上消除了这些隐藏单元的许多影响。如果是这种情况，这个被大大简化了的神经网络会变成一个很小的网络，小到如同一个逻辑回归单元，可是深度却很大，它会使这个网络从过度拟合的状态更接近左图的高偏差状态。

但是会存在一个中间值，于是会有一个接近“Just Right”的中间状态。

如果增加到足够大，会接近于0，实际上是不会发生这种情况的，我们尝试消除或至少减少许多隐藏单元的影响，最终这个网络会变得更简单，这个神经网络越来越接近逻辑回归，我们直觉上认为大量隐藏单元被完全消除了，其实不然，实际上是该神经网络的所有隐藏单元依然存在，但是它们的影响变得更小了。神经网络变得更简单了，貌似这样更不容易发生过拟合，因此我不确定这个直觉经验是否有用，不过在编程中执行正则化时，你实际看到一些方差减少的结果。

我们进入到神经网络内部来直观感受下为什么正则化会预防过拟合的问题，假设我们采用了tanh的双曲线激活函数

如果使用了正则化部分，那么权重W会倾向于更小，因此得到的 z=w*A+b会更小，在作用在激活函数的时候会接近于上图中横轴零点左右的部分，如下图所示：

如果 z的值最终在这个范围内，都是相对较小的值，g（z）=tanh（z）大致呈线性，每层几乎都是线性的，和线性回归函数一样。如果每层都是线性的，那么整个网络就是一个线性网络，即使是一个非常深的深层网络，因具有线性激活函数的特征，最终我们只能计算线性函数，因此，它不适用于非常复杂的决策，以及过度拟合数据集的非线性决策边界。

layers.Dense(32, activation='sigmoid')
layers.Dense(32, activation=tf.sigmoid)
layers.Dense(32, kernel_initializer='orthogonal')
layers.Dense(32, kernel_initializer=tf.keras.initializers.glorot_normal)
layers.Dense(32, kernel_regularizer=tf.keras.regularizers.l2(0.01))
layers.Dense(32, kernel_regularizer=tf.keras.regularizers.l1(0.01))

3 训练和评估

3.1 设置训练流程

构建好模型后，通过调用 compile 方法配置该模型的学习流程：

model = tf.keras.Sequential()
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(32, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
             loss=tf.keras.losses.categorical_crossentropy,
             metrics=[tf.keras.metrics.categorical_accuracy])

网络模型搭建完后，需要对网络的学习过程进行配置，否则在调用fit或evaluate时会抛出异常。可以使用 compile(self, optimizer, loss, metrics=None, sample_weight_mode=None, weighted_metrics=None, target_tensors=None) 来完成配置
compile() 主要接收前三个参数：

loss：字符串类型，用来指定损失函数，如：categorical_crossentropy，binary_crossentropy
optimizer：字符串类型，用来指定优化方式，如：rmsprop，adam，sgd
metrics：列表类型，用来指定衡量模型的指标，如：accuracy
model.compile(loss=‘categorical_crossentropy’, optimizer=‘sgd’, metrics=[‘accuracy’])
还可以加入其他回调函数，后面会讲到

3.2 输入Numpy数据

对于小型数据集，可以使用Numpy构建输入数据。

在这里，我们瞎编一些数据，这些瞎编的数据可以让我们的网络开始训练，但是注定不会训练出结果

import numpy as np

train_x = np.random.random((1000, 72))
train_y = np.random.random((1000, 10))

val_x = np.random.random((200, 72))
val_y = np.random.random((200, 10))

model.fit(train_x, train_y, epochs=100, batch_size=100,
          validation_data=(val_x, val_y))

Train on 1000 samples, validate on 200 samples
Epoch 1/100
1000/1000 [==============================] - 1s 639us/sample - loss: 12.1864 - categorical_accuracy: 0.1070 - val_loss: 12.2439 - val_categorical_accuracy: 0.0600
Epoch 2/100
1000/1000 [==============================] - 0s 27us/sample - loss: 13.0292 - categorical_accuracy: 0.0950 - val_loss: 13.7217 - val_categorical_accuracy: 0.0650
Epoch 3/100
1000/1000 [==============================] - 0s 25us/sample - loss: 15.0484 - categorical_accuracy: 0.0930 - val_loss: 16.4090 - val_categorical_accuracy: 0.0650
Epoch 4/100
1000/1000 [==============================] - 0s 26us/sample - loss: 18.0353 - categorical_accuracy: 0.0930 - val_loss: 19.7006 - val_categorical_accuracy: 0.0650
Epoch 5/100
1000/1000 [==============================] - 0s 25us/sample - loss: 21.6455 - categorical_accuracy: 0.0930 - val_loss: 24.1038 - val_categorical_accuracy: 0.0650
Epoch 6/100
1000/1000 [==============================] - 0s 25us/sample - loss: 27.2545 - categorical_accuracy: 0.0930 - val_loss: 31.3219 - val_categorical_accuracy: 0.0850
Epoch 7/100
1000/1000 [==============================] - 0s 25us/sample - loss: 35.5471 - categorical_accuracy: 0.0980 - val_loss: 41.1936 - val_categorical_accuracy: 0.0850
Epoch 8/100
1000/1000 [==============================] - 0s 26us/sample - loss: 46.7873 - categorical_accuracy: 0.0940 - val_loss: 54.2268 - val_categorical_accuracy: 0.0850
Epoch 9/100
1000/1000 [==============================] - 0s 54us/sample - loss: 61.4755 - categorical_accuracy: 0.0950 - val_loss: 70.8410 - val_categorical_accuracy: 0.0700
Epoch 10/100
1000/1000 [==============================] - 0s 25us/sample - loss: 79.4868 - categorical_accuracy: 0.0950 - val_loss: 90.7648 - val_categorical_accuracy: 0.0700
Epoch 11/100
1000/1000 [==============================] - 0s 25us/sample - loss: 101.1739 - categorical_accuracy: 0.0900 - val_loss: 114.7025 - val_categorical_accuracy: 0.0700
Epoch 12/100
1000/1000 [==============================] - 0s 25us/sample - loss: 126.8959 - categorical_accuracy: 0.0930 - val_loss: 142.6307 - val_categorical_accuracy: 0.0700
Epoch 13/100
1000/1000 [==============================] - 0s 26us/sample - loss: 156.6893 - categorical_accuracy: 0.0960 - val_loss: 174.7227 - val_categorical_accuracy: 0.0750
Epoch 14/100
1000/1000 [==============================] - 0s 25us/sample - loss: 190.8326 - categorical_accuracy: 0.0960 - val_loss: 211.4004 - val_categorical_accuracy: 0.0650
Epoch 15/100
1000/1000 [==============================] - 0s 26us/sample - loss: 229.5933 - categorical_accuracy: 0.0920 - val_loss: 252.9706 - val_categorical_accuracy: 0.0750
Epoch 16/100
1000/1000 [==============================] - 0s 55us/sample - loss: 273.4981 - categorical_accuracy: 0.0960 - val_loss: 299.2311 - val_categorical_accuracy: 0.0700
Epoch 17/100
1000/1000 [==============================] - 0s 25us/sample - loss: 321.7867 - categorical_accuracy: 0.0980 - val_loss: 349.4678 - val_categorical_accuracy: 0.0700
Epoch 18/100
1000/1000 [==============================] - 0s 25us/sample - loss: 373.7236 - categorical_accuracy: 0.0890 - val_loss: 403.5012 - val_categorical_accuracy: 0.0700
Epoch 19/100
1000/1000 [==============================] - 0s 25us/sample - loss: 430.0553 - categorical_accuracy: 0.0970 - val_loss: 461.5726 - val_categorical_accuracy: 0.0550
Epoch 20/100
1000/1000 [==============================] - 0s 25us/sample - loss: 490.2736 - categorical_accuracy: 0.0970 - val_loss: 523.4989 - val_categorical_accuracy: 0.0650
Epoch 21/100
1000/1000 [==============================] - 0s 24us/sample - loss: 553.6836 - categorical_accuracy: 0.0980 - val_loss: 589.3144 - val_categorical_accuracy: 0.0950
Epoch 22/100
1000/1000 [==============================] - 0s 28us/sample - loss: 620.6393 - categorical_accuracy: 0.0980 - val_loss: 657.2309 - val_categorical_accuracy: 0.0650
Epoch 23/100
1000/1000 [==============================] - 0s 52us/sample - loss: 689.7130 - categorical_accuracy: 0.0990 - val_loss: 727.0188 - val_categorical_accuracy: 0.0700
Epoch 24/100
1000/1000 [==============================] - 0s 26us/sample - loss: 762.0412 - categorical_accuracy: 0.0970 - val_loss: 801.4167 - val_categorical_accuracy: 0.0900
Epoch 25/100
1000/1000 [==============================] - 0s 25us/sample - loss: 834.9594 - categorical_accuracy: 0.0960 - val_loss: 872.5280 - val_categorical_accuracy: 0.0900
Epoch 26/100
1000/1000 [==============================] - 0s 25us/sample - loss: 906.5170 - categorical_accuracy: 0.1030 - val_loss: 943.2008 - val_categorical_accuracy: 0.0600
Epoch 27/100
1000/1000 [==============================] - 0s 25us/sample - loss: 975.0647 - categorical_accuracy: 0.0920 - val_loss: 1009.4395 - val_categorical_accuracy: 0.0650
Epoch 28/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1040.0404 - categorical_accuracy: 0.1020 - val_loss: 1073.9507 - val_categorical_accuracy: 0.0800
Epoch 29/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1104.9380 - categorical_accuracy: 0.1120 - val_loss: 1137.9870 - val_categorical_accuracy: 0.0950
Epoch 30/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1168.8721 - categorical_accuracy: 0.1170 - val_loss: 1202.9854 - val_categorical_accuracy: 0.0950
Epoch 31/100
1000/1000 [==============================] - 0s 55us/sample - loss: 1234.6194 - categorical_accuracy: 0.0960 - val_loss: 1267.8508 - val_categorical_accuracy: 0.0850
Epoch 32/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1301.6757 - categorical_accuracy: 0.0990 - val_loss: 1336.4615 - val_categorical_accuracy: 0.0700
Epoch 33/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1367.7428 - categorical_accuracy: 0.1060 - val_loss: 1402.0927 - val_categorical_accuracy: 0.1000
Epoch 34/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1432.2028 - categorical_accuracy: 0.1030 - val_loss: 1463.5681 - val_categorical_accuracy: 0.0650
Epoch 35/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1497.1898 - categorical_accuracy: 0.1040 - val_loss: 1529.4269 - val_categorical_accuracy: 0.0950
Epoch 36/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1559.5742 - categorical_accuracy: 0.1010 - val_loss: 1588.0530 - val_categorical_accuracy: 0.0550
Epoch 37/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1611.4853 - categorical_accuracy: 0.1010 - val_loss: 1636.0344 - val_categorical_accuracy: 0.0650
Epoch 38/100
1000/1000 [==============================] - 0s 52us/sample - loss: 1642.6731 - categorical_accuracy: 0.1010 - val_loss: 1627.1154 - val_categorical_accuracy: 0.0700
Epoch 39/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1606.4901 - categorical_accuracy: 0.1060 - val_loss: 1573.7168 - val_categorical_accuracy: 0.0750
Epoch 40/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1552.0087 - categorical_accuracy: 0.0960 - val_loss: 1517.2331 - val_categorical_accuracy: 0.1050
Epoch 41/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1484.4402 - categorical_accuracy: 0.0990 - val_loss: 1465.9717 - val_categorical_accuracy: 0.0950
Epoch 42/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1476.1709 - categorical_accuracy: 0.0970 - val_loss: 1470.3436 - val_categorical_accuracy: 0.0900
Epoch 43/100
1000/1000 [==============================] - 0s 24us/sample - loss: 1472.6699 - categorical_accuracy: 0.1140 - val_loss: 1471.9978 - val_categorical_accuracy: 0.0700
Epoch 44/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1466.9905 - categorical_accuracy: 0.1040 - val_loss: 1460.1993 - val_categorical_accuracy: 0.1000
Epoch 45/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1459.5785 - categorical_accuracy: 0.0910 - val_loss: 1452.8042 - val_categorical_accuracy: 0.1000
Epoch 46/100
1000/1000 [==============================] - 0s 56us/sample - loss: 1447.0048 - categorical_accuracy: 0.0960 - val_loss: 1432.1102 - val_categorical_accuracy: 0.0600
Epoch 47/100
1000/1000 [==============================] - 0s 27us/sample - loss: 1418.5652 - categorical_accuracy: 0.1060 - val_loss: 1398.0585 - val_categorical_accuracy: 0.0650
Epoch 48/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1380.7618 - categorical_accuracy: 0.1160 - val_loss: 1358.1672 - val_categorical_accuracy: 0.0700
Epoch 49/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1338.6998 - categorical_accuracy: 0.1000 - val_loss: 1310.9040 - val_categorical_accuracy: 0.0750
Epoch 50/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1300.4685 - categorical_accuracy: 0.0950 - val_loss: 1294.6734 - val_categorical_accuracy: 0.1050
Epoch 51/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1289.1089 - categorical_accuracy: 0.1030 - val_loss: 1287.9561 - val_categorical_accuracy: 0.0600
Epoch 52/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1275.6635 - categorical_accuracy: 0.1000 - val_loss: 1265.8784 - val_categorical_accuracy: 0.0600
Epoch 53/100
1000/1000 [==============================] - 0s 32us/sample - loss: 1244.8945 - categorical_accuracy: 0.0970 - val_loss: 1233.3094 - val_categorical_accuracy: 0.1050
Epoch 54/100
1000/1000 [==============================] - 0s 47us/sample - loss: 1229.7360 - categorical_accuracy: 0.1080 - val_loss: 1213.3581 - val_categorical_accuracy: 0.0600
Epoch 55/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1204.4045 - categorical_accuracy: 0.1000 - val_loss: 1182.9891 - val_categorical_accuracy: 0.1050
Epoch 56/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1178.2038 - categorical_accuracy: 0.0880 - val_loss: 1160.3662 - val_categorical_accuracy: 0.0900
Epoch 57/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1149.1897 - categorical_accuracy: 0.0980 - val_loss: 1129.1326 - val_categorical_accuracy: 0.1050
Epoch 58/100
1000/1000 [==============================] - 0s 25us/sample - loss: 1114.6702 - categorical_accuracy: 0.1070 - val_loss: 1094.9047 - val_categorical_accuracy: 0.0600
Epoch 59/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1074.4851 - categorical_accuracy: 0.1100 - val_loss: 1040.2871 - val_categorical_accuracy: 0.0600
Epoch 60/100
1000/1000 [==============================] - 0s 26us/sample - loss: 1034.7077 - categorical_accuracy: 0.0970 - val_loss: 985.9434 - val_categorical_accuracy: 0.1000
Epoch 61/100
1000/1000 [==============================] - 0s 53us/sample - loss: 976.7049 - categorical_accuracy: 0.1100 - val_loss: 933.5067 - val_categorical_accuracy: 0.1100
Epoch 62/100
1000/1000 [==============================] - 0s 25us/sample - loss: 911.3713 - categorical_accuracy: 0.1010 - val_loss: 853.1591 - val_categorical_accuracy: 0.0650
Epoch 63/100
1000/1000 [==============================] - 0s 25us/sample - loss: 842.8447 - categorical_accuracy: 0.1000 - val_loss: 789.3255 - val_categorical_accuracy: 0.1100
Epoch 64/100
1000/1000 [==============================] - 0s 25us/sample - loss: 775.2145 - categorical_accuracy: 0.0970 - val_loss: 722.6735 - val_categorical_accuracy: 0.0650
Epoch 65/100
1000/1000 [==============================] - 0s 25us/sample - loss: 726.7562 - categorical_accuracy: 0.1070 - val_loss: 698.1979 - val_categorical_accuracy: 0.0600
Epoch 66/100
1000/1000 [==============================] - 0s 25us/sample - loss: 717.8865 - categorical_accuracy: 0.1080 - val_loss: 690.8430 - val_categorical_accuracy: 0.1150
Epoch 67/100
1000/1000 [==============================] - 0s 25us/sample - loss: 703.6470 - categorical_accuracy: 0.1020 - val_loss: 668.8605 - val_categorical_accuracy: 0.1100
Epoch 68/100
1000/1000 [==============================] - 0s 26us/sample - loss: 677.8014 - categorical_accuracy: 0.1130 - val_loss: 658.3235 - val_categorical_accuracy: 0.0600
Epoch 69/100
1000/1000 [==============================] - 0s 55us/sample - loss: 675.8244 - categorical_accuracy: 0.0970 - val_loss: 629.1815 - val_categorical_accuracy: 0.1100
Epoch 70/100
1000/1000 [==============================] - 0s 25us/sample - loss: 653.8402 - categorical_accuracy: 0.0920 - val_loss: 628.9182 - val_categorical_accuracy: 0.1300
Epoch 71/100
1000/1000 [==============================] - 0s 26us/sample - loss: 649.8070 - categorical_accuracy: 0.0970 - val_loss: 600.7431 - val_categorical_accuracy: 0.0600
Epoch 72/100
1000/1000 [==============================] - 0s 25us/sample - loss: 603.2672 - categorical_accuracy: 0.1160 - val_loss: 574.3532 - val_categorical_accuracy: 0.1050
Epoch 73/100
1000/1000 [==============================] - 0s 25us/sample - loss: 584.7944 - categorical_accuracy: 0.1070 - val_loss: 568.0578 - val_categorical_accuracy: 0.1000
Epoch 74/100
1000/1000 [==============================] - 0s 25us/sample - loss: 568.6435 - categorical_accuracy: 0.1030 - val_loss: 527.7212 - val_categorical_accuracy: 0.0650
Epoch 75/100
1000/1000 [==============================] - 0s 25us/sample - loss: 526.5512 - categorical_accuracy: 0.1050 - val_loss: 479.1668 - val_categorical_accuracy: 0.1000
Epoch 76/100
1000/1000 [==============================] - 0s 26us/sample - loss: 509.3205 - categorical_accuracy: 0.1000 - val_loss: 493.5508 - val_categorical_accuracy: 0.1050
Epoch 77/100
1000/1000 [==============================] - 0s 52us/sample - loss: 456.1215 - categorical_accuracy: 0.1070 - val_loss: 401.0019 - val_categorical_accuracy: 0.1000
Epoch 78/100
1000/1000 [==============================] - 0s 25us/sample - loss: 403.5868 - categorical_accuracy: 0.0980 - val_loss: 350.1806 - val_categorical_accuracy: 0.1050
Epoch 79/100
1000/1000 [==============================] - 0s 26us/sample - loss: 345.5986 - categorical_accuracy: 0.0990 - val_loss: 311.8484 - val_categorical_accuracy: 0.1100
Epoch 80/100
1000/1000 [==============================] - 0s 26us/sample - loss: 285.0324 - categorical_accuracy: 0.0960 - val_loss: 258.4336 - val_categorical_accuracy: 0.1050
Epoch 81/100
1000/1000 [==============================] - 0s 26us/sample - loss: 250.0112 - categorical_accuracy: 0.1070 - val_loss: 187.9330 - val_categorical_accuracy: 0.0900
Epoch 82/100
1000/1000 [==============================] - 0s 26us/sample - loss: 192.5750 - categorical_accuracy: 0.1160 - val_loss: 140.8783 - val_categorical_accuracy: 0.1100
Epoch 83/100
1000/1000 [==============================] - 0s 25us/sample - loss: 146.9630 - categorical_accuracy: 0.1090 - val_loss: 121.0113 - val_categorical_accuracy: 0.0750
Epoch 84/100
1000/1000 [==============================] - 0s 56us/sample - loss: 115.7717 - categorical_accuracy: 0.0860 - val_loss: 75.5320 - val_categorical_accuracy: 0.1000
Epoch 85/100
1000/1000 [==============================] - 0s 26us/sample - loss: 105.5616 - categorical_accuracy: 0.0950 - val_loss: 122.1138 - val_categorical_accuracy: 0.1050
Epoch 86/100
1000/1000 [==============================] - 0s 25us/sample - loss: 100.0362 - categorical_accuracy: 0.1080 - val_loss: 108.7261 - val_categorical_accuracy: 0.1350
Epoch 87/100
1000/1000 [==============================] - 0s 25us/sample - loss: 127.4710 - categorical_accuracy: 0.1090 - val_loss: 132.0981 - val_categorical_accuracy: 0.0650
Epoch 88/100
1000/1000 [==============================] - 0s 25us/sample - loss: 141.0293 - categorical_accuracy: 0.1020 - val_loss: 133.2474 - val_categorical_accuracy: 0.1350
Epoch 89/100
1000/1000 [==============================] - 0s 26us/sample - loss: 120.4979 - categorical_accuracy: 0.1150 - val_loss: 117.8078 - val_categorical_accuracy: 0.1000
Epoch 90/100
1000/1000 [==============================] - 0s 25us/sample - loss: 119.5986 - categorical_accuracy: 0.1060 - val_loss: 92.7652 - val_categorical_accuracy: 0.1350
Epoch 91/100
1000/1000 [==============================] - 0s 56us/sample - loss: 104.3861 - categorical_accuracy: 0.0930 - val_loss: 75.7607 - val_categorical_accuracy: 0.0600
Epoch 92/100
1000/1000 [==============================] - 0s 26us/sample - loss: 125.5138 - categorical_accuracy: 0.0900 - val_loss: 141.1569 - val_categorical_accuracy: 0.0950
Epoch 93/100
1000/1000 [==============================] - 0s 26us/sample - loss: 176.3270 - categorical_accuracy: 0.0840 - val_loss: 187.2577 - val_categorical_accuracy: 0.1300
Epoch 94/100
1000/1000 [==============================] - 0s 26us/sample - loss: 147.3037 - categorical_accuracy: 0.1100 - val_loss: 125.9804 - val_categorical_accuracy: 0.1100
Epoch 95/100
1000/1000 [==============================] - 0s 26us/sample - loss: 165.9997 - categorical_accuracy: 0.1060 - val_loss: 107.8639 - val_categorical_accuracy: 0.1350
Epoch 96/100
1000/1000 [==============================] - 0s 26us/sample - loss: 163.7285 - categorical_accuracy: 0.0990 - val_loss: 159.1753 - val_categorical_accuracy: 0.0650
Epoch 97/100
1000/1000 [==============================] - 0s 27us/sample - loss: 145.3247 - categorical_accuracy: 0.1110 - val_loss: 121.4570 - val_categorical_accuracy: 0.1350
Epoch 98/100
1000/1000 [==============================] - 0s 53us/sample - loss: 139.6124 - categorical_accuracy: 0.0960 - val_loss: 141.9158 - val_categorical_accuracy: 0.0650
Epoch 99/100
1000/1000 [==============================] - 0s 27us/sample - loss: 122.9475 - categorical_accuracy: 0.1140 - val_loss: 91.3999 - val_categorical_accuracy: 0.0650
Epoch 100/100
1000/1000 [==============================] - 0s 26us/sample - loss: 135.1131 - categorical_accuracy: 0.0840 - val_loss: 114.3255 - val_categorical_accuracy: 0.1050

3.3 tf.data输入数据

对于大型数据集可以使用tf.data构建训练输入。

一般来说，我们训练网络的数据维度很大，数据量也很多，所以要用tf.data来管理，提高读写效率

dataset = tf.data.Dataset.from_tensor_slices((train_x, train_y))
dataset = dataset.batch(32)
dataset = dataset.repeat() #防止循环次数*batch大于数据总量的情况下报错
val_dataset = tf.data.Dataset.from_tensor_slices((val_x, val_y))
val_dataset = val_dataset.batch(32)
val_dataset = val_dataset.repeat()

model.fit(dataset, epochs=10, steps_per_epoch=30,
          validation_data=val_dataset, validation_steps=3)

Train for 30 steps, validate for 3 steps
Epoch 1/10
30/30 [==============================] - 0s 10ms/step - loss: 162.7071 - categorical_accuracy: 0.0948 - val_loss: 132.7141 - val_categorical_accuracy: 0.0625
Epoch 2/10
30/30 [==============================] - 0s 3ms/step - loss: 151.5471 - categorical_accuracy: 0.1026 - val_loss: 156.8644 - val_categorical_accuracy: 0.0833
Epoch 3/10
30/30 [==============================] - 0s 2ms/step - loss: 149.6497 - categorical_accuracy: 0.1004 - val_loss: 157.7960 - val_categorical_accuracy: 0.0521
Epoch 4/10
30/30 [==============================] - 0s 2ms/step - loss: 185.5166 - categorical_accuracy: 0.0994 - val_loss: 147.6869 - val_categorical_accuracy: 0.1146
Epoch 5/10
30/30 [==============================] - 0s 3ms/step - loss: 233.9934 - categorical_accuracy: 0.0994 - val_loss: 261.1310 - val_categorical_accuracy: 0.0938
Epoch 6/10
30/30 [==============================] - 0s 2ms/step - loss: 248.8591 - categorical_accuracy: 0.0919 - val_loss: 153.8509 - val_categorical_accuracy: 0.1146
Epoch 7/10
30/30 [==============================] - 0s 3ms/step - loss: 260.5320 - categorical_accuracy: 0.1004 - val_loss: 254.9412 - val_categorical_accuracy: 0.0938
Epoch 8/10
30/30 [==============================] - 0s 2ms/step - loss: 192.3668 - categorical_accuracy: 0.0972 - val_loss: 203.8111 - val_categorical_accuracy: 0.1146
Epoch 9/10
30/30 [==============================] - 0s 2ms/step - loss: 227.1097 - categorical_accuracy: 0.0951 - val_loss: 241.0869 - val_categorical_accuracy: 0.1354
Epoch 10/10
30/30 [==============================] - 0s 3ms/step - loss: 267.9791 - categorical_accuracy: 0.0791 - val_loss: 209.5756 - val_categorical_accuracy: 0.1146

基于 tf.data API，我们可以使用简单的代码来构建复杂的输入 pipeline。
例如，从分布式文件系统中读取数据、进行预处理、合成为 batch、训练中使用数据集；
或者，文本模型的输入 pipeline 需要从原始文本数据中提取符号、根据对照表将其转换为嵌入标识符，以及将不同长度的序列组合成batch数据等。
使用 tf.data API 可以轻松处理大量数据、不同的数据格式以及复杂的转换。
tf.data API 在 TensorFlow 中引入了两个新概念：
（1）tf.data.Dataset：表示一系列元素，其中每个元素包含一个或多个 Tensor 对象。例如，在图片管道中，一个元素可能是单个训练样本，具有一对表示图片数据和标签的张量。可以通过两种不同的方式来创建数据集。

 直接从 Tensor 创建 Dataset（例如 Dataset.from_tensor_slices()）；当然 Numpy 也是可以的，TensorFlow 会自动将其转换为 Tensor。

通过对一个或多个 tf.data.Dataset 对象来使用变换（例如 Dataset.batch()）来创建 Dataset

（2）tf.data.Iterator：这是从数据集中提取元素的主要方法。Iterator.get_next() 指令会在执行时生成 Dataset 的下一个元素，并且此指令通常充当输入管道和模型之间的接口。最简单的迭代器是“单次迭代器”，它会对处理好的 Dataset 进行单次迭代。要实现更复杂的用途，您可以通过 Iterator.initializer 指令使用不同的数据集重新初始化和参数化迭代器，这样一来，您就可以在同一个程序中对训练和验证数据进行多次迭代（举例而言）。

一个 Dataset 对象包含多个元素，每个元素的结构都相同。每个元素包含一个或多个 tf.Tensor 对象，这些对象被称为组件。每个组件都有 tf.DType 属性，表示 Tensor 中元素的类型；以及 tf.TensorShape 属性，表示每个元素（可能部分指定）的静态形状。您可以通过 Dataset.output_types 和 Dataset.output_shapes 属性检查数据集元素各个组件的类型和形状。Dataset 的属性由构成该 Dataset 的元素的属性映射得到，元素可以是单个张量、张量元组，也可以是张量的嵌套元组。例如：

dataset1 = tf.data.Dataset.from_tensor_slices(tf.random.uniform([4, 10]))
print(dataset1)  # ==> "tf.float32"
 
dataset2 = tf.data.Dataset.from_tensor_slices(
   (tf.random.uniform([4]),
    tf.random.uniform([4, 100], maxval=100, dtype=tf.int32)))
print(dataset2)  # ==> "(tf.float32, tf.int32)"
 
dataset3 = tf.data.Dataset.zip((dataset1, dataset2))
print(dataset3)  # ==> (tf.float32, (tf.float32, tf.int32))

print(list(dataset3.take(1)))

[(, (, ))]

3.4 评估与预测

评估和预测函数：tf.keras.Model.evaluate和tf.keras.Model.predict方法，都可以可以使用NumPy和tf.data.Dataset构造的输入数据进行评估和预测
评估与预测的目的是不同的。
我们可以看到，准确率惨不忍睹，因为我们用来训练的数据肯本就不是一个可训练的数据

# 模型评估
test_x = np.random.random((1000, 72))
test_y = np.random.random((1000, 10))
model.evaluate(test_x, test_y, batch_size=32)
test_data = tf.data.Dataset.from_tensor_slices((test_x, test_y))
test_data = test_data.batch(32).repeat()
model.evaluate(test_data, steps=30)

1000/1000 [==============================] - 0s 153us/sample - loss: 210.7485 - categorical_accuracy: 0.0990
30/30 [==============================] - 0s 2ms/step - loss: 210.3705 - categorical_accuracy: 0.0969





[210.37054392496745, 0.096875]

# 模型预测
result = model.predict(test_x, batch_size=32)
print(result)

[[2.3885893e-13 3.6062306e-14 3.4597181e-04 ... 1.7771703e-05
  3.9381185e-13 9.9959689e-01]
 [5.8199810e-13 1.8029461e-13 3.8594753e-04 ... 1.5929958e-05
  1.5820349e-12 9.9956590e-01]
 [4.2835317e-14 1.3064033e-14 1.4652881e-04 ... 4.7101612e-06
  2.4650025e-13 9.9983656e-01]
 ...
 [5.8543299e-14 2.9437414e-14 2.3781681e-04 ... 7.5260905e-06
  2.9730737e-13 9.9974018e-01]
 [1.6417090e-13 9.9574679e-14 3.1998276e-04 ... 2.0455815e-05
  1.0056686e-12 9.9963164e-01]
 [1.0115633e-13 3.9613386e-14 2.0342070e-04 ... 1.2408743e-05
  8.3384054e-13 9.9976581e-01]]

4 构建复杂模型

4.1 函数式API

tf.keras.Sequential 模型是层的简单堆叠，无法表示任意模型。使用 Keras的函数式API可以构建复杂的模型拓扑，例如：

• 多输入模型，

• 多输出模型，

• 具有共享层的模型（同一层被调用多次），

• 具有非序列数据流的模型（例如，残差连接）。

使用函数式 API 构建的模型具有以下特征：

• 层实例可调用并返回张量。
• 输入张量和输出张量用于定义 tf.keras.Model 实例。
• 此模型的训练方式和 Sequential 模型一样。

input_x = tf.keras.Input(shape=(72,))
hidden1 = layers.Dense(32, activation='relu')(input_x)
hidden2 = layers.Dense(16, activation='relu')(hidden1)
pred = layers.Dense(10, activation='softmax')(hidden2)
# 构建tf.keras.Model实例
model = tf.keras.Model(inputs=input_x, outputs=pred)
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
             loss=tf.keras.losses.categorical_crossentropy,
             metrics=['accuracy'])
model.fit(train_x, train_y, batch_size=32, epochs=5)

Train on 1000 samples
Epoch 1/5
1000/1000 [==============================] - 0s 351us/sample - loss: 12.2272 - accuracy: 0.0990
Epoch 2/5
1000/1000 [==============================] - 0s 65us/sample - loss: 18.5298 - accuracy: 0.0850
Epoch 3/5
1000/1000 [==============================] - 0s 91us/sample - loss: 33.0864 - accuracy: 0.0940
Epoch 4/5
1000/1000 [==============================] - 0s 66us/sample - loss: 56.0615 - accuracy: 0.0940
Epoch 5/5
1000/1000 [==============================] - 0s 65us/sample - loss: 88.7252 - accuracy: 0.0880

4.2 模型子类化

可以通过对 tf.keras.Model 进行子类化并定义自己的前向传播来构建完全可自定义的模型。

• 在_init_ 方法中创建层并将它们设置为类实例的属性。
• 在__call__方法中定义前向传播

class MyModel(tf.keras.Model):
    def __init__(self, num_classes=10):
        super(MyModel, self).__init__(name='my_model')
        self.num_classes = num_classes
        # 定义网络层
        self.layer1 = layers.Dense(32, activation='relu')
        self.layer2 = layers.Dense(num_classes, activation='softmax')
    def call(self, inputs):
        # 定义前向传播
        h1 = self.layer1(inputs)
        out = self.layer2(h1)
        return out
    
    def compute_output_shape(self, input_shape):
        # 计算输出shape
        shape = tf.TensorShape(input_shape).as_list()
        shape[-1] = self.num_classes
        return tf.TensorShape(shape)
# 实例化模型类，并训练
model = MyModel(num_classes=10)
model.compile(optimizer=tf.keras.optimizers.RMSprop(0.001),
             loss=tf.keras.losses.categorical_crossentropy,
             metrics=['accuracy'])

model.fit(train_x, train_y, batch_size=16, epochs=5)

Train on 1000 samples
Epoch 1/5
1000/1000 [==============================] - 0s 453us/sample - loss: 13.3207 - accuracy: 0.1050
Epoch 2/5
1000/1000 [==============================] - 0s 163us/sample - loss: 15.3926 - accuracy: 0.1040
Epoch 3/5
1000/1000 [==============================] - 0s 135us/sample - loss: 17.8175 - accuracy: 0.1050
Epoch 4/5
1000/1000 [==============================] - 0s 163us/sample - loss: 20.3278 - accuracy: 0.1060
Epoch 5/5
1000/1000 [==============================] - 0s 167us/sample - loss: 23.4035 - accuracy: 0.1070

4.3 自定义层

通过对 tf.keras.layers.Layer 进行子类化并实现以下方法来创建自定义层：

• _init_: (可选)定义该层要使用的子层

• build：创建层的权重。使用 add_weight 方法添加权重。

• call：定义前向传播。

• compute_output_shape：指定在给定输入形状的情况下如何计算层的输出形状。

• 可选，可以通过实现 get_config 方法和 from_config 类方法序列化层。

class MyLayer(layers.Layer):
    def __init__(self, output_dim, **kwargs):
        self.output_dim = output_dim
        super(MyLayer, self).__init__(**kwargs)
    
    def build(self, input_shape):
        shape = tf.TensorShape((input_shape[1], self.output_dim))
        self.kernel = self.add_weight(name='kernel1', shape=shape,
                                   initializer='uniform', trainable=True)
        super(MyLayer, self).build(input_shape)
    
    def call(self, inputs):
        return tf.matmul(inputs, self.kernel)

    def compute_output_shape(self, input_shape):
        shape = tf.TensorShape(input_shape).as_list()
        shape[-1] = self.output_dim
        return tf.TensorShape(shape)

    def get_config(self):
        base_config = super(MyLayer, self).get_config()
        base_config['output_dim'] = self.output_dim
        return base_config

    @classmethod
    def from_config(cls, config):
        return cls(**config)

# 使用自定义网络层构建模型
model = tf.keras.Sequential(
[
    MyLayer(10),
    layers.Activation('softmax')
])


model.compile(optimizer=tf.keras.optimizers.RMSprop(0.001),
             loss=tf.keras.losses.categorical_crossentropy,
             metrics=['accuracy'])

model.fit(train_x, train_y, batch_size=16, epochs=5)
model.summary()
        

Train on 1000 samples
Epoch 1/5
1000/1000 [==============================] - 0s 377us/sample - loss: 11.6191 - accuracy: 0.1030
Epoch 2/5
1000/1000 [==============================] - 0s 144us/sample - loss: 11.6184 - accuracy: 0.1060
Epoch 3/5
1000/1000 [==============================] - 0s 115us/sample - loss: 11.6159 - accuracy: 0.1040
Epoch 4/5
1000/1000 [==============================] - 0s 141us/sample - loss: 11.6138 - accuracy: 0.1000
Epoch 5/5
1000/1000 [==============================] - 0s 113us/sample - loss: 11.6103 - accuracy: 0.1010
Model: "sequential_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
my_layer (MyLayer)           multiple                  720       
_________________________________________________________________
activation (Activation)      multiple                  0         
=================================================================
Total params: 720
Trainable params: 720
Non-trainable params: 0
_________________________________________________________________

4.3 回调

回调是传递给模型以自定义和扩展其在训练期间的行为的对象。我们可以编写自己的自定义回调，或使用tf.keras.callbacks中的内置函数，常用内置回调函数如下：

• tf.keras.callbacks.ModelCheckpoint：定期保存模型的检查点。
• tf.keras.callbacks.LearningRateScheduler：动态更改学习率。
• tf.keras.callbacks.EarlyStopping：验证性能停止提高时进行中断培训。
• tf.keras.callbacks.TensorBoard：使用TensorBoard监视模型的行为 。

%load_ext tensorboard

logdir="./tb/" + datetime.now().strftime("%Y%m%d-%H%M%S")

callbacks = [
    tf.keras.callbacks.EarlyStopping(patience=2, monitor='val_loss'),
    tf.keras.callbacks.TensorBoard(log_dir=logdir)
]
model.fit(train_x, train_y, batch_size=16, epochs=5,
         callbacks=callbacks, validation_data=(val_x, val_y))
%tensorboard --logdir tb/ --host=0.0.0.0

Train on 1000 samples, validate on 200 samples
Epoch 1/5
1000/1000 [==============================] - 0s 348us/sample - loss: 11.6089 - accuracy: 0.1040 - val_loss: 11.3648 - val_accuracy: 0.0950
Epoch 2/5
1000/1000 [==============================] - 0s 198us/sample - loss: 11.6075 - accuracy: 0.1010 - val_loss: 11.3608 - val_accuracy: 0.1000
Epoch 3/5
1000/1000 [==============================] - 0s 202us/sample - loss: 11.6062 - accuracy: 0.1060 - val_loss: 11.3627 - val_accuracy: 0.0950
Epoch 4/5
1000/1000 [==============================] - 0s 203us/sample - loss: 11.6062 - accuracy: 0.1020 - val_loss: 11.3591 - val_accuracy: 0.1100
Epoch 5/5
1000/1000 [==============================] - 0s 201us/sample - loss: 11.6032 - accuracy: 0.1030 - val_loss: 11.3598 - val_accuracy: 0.1000

5 模型保存与恢复

5.1 权重保存

model = tf.keras.Sequential([
layers.Dense(64, activation='relu', input_shape=(32,)),  # 需要有input_shape
layers.Dense(10, activation='softmax')])

model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
              loss='categorical_crossentropy',
              metrics=['accuracy'])

# 权重保存与重载
model.save_weights('./weights/model')
model.load_weights('./weights/model')
# 保存为h5格式
model.save_weights('./model.h5', save_format='h5')
model.load_weights('./model.h5')

5.2 保存网络结构

# 序列化成json
import json
import pprint
json_str = model.to_json()
pprint.pprint(json.loads(json_str))
# 从json中重建模型
fresh_model = tf.keras.models.model_from_json(json_str)

# 保持为yaml格式  #需要提前安装pyyaml

yaml_str = model.to_yaml()
print(yaml_str)
# 从yaml数据中重新构建模型
fresh_model = tf.keras.models.model_from_yaml(yaml_str)

注意：子类模型不可序列化，因为其体系结构由call方法主体中的Python代码定义。

5.3 保存整个模型

model = tf.keras.Sequential([
  layers.Dense(10, activation='softmax', input_shape=(72,)),
  layers.Dense(10, activation='softmax')
])
model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])
model.fit(train_x, train_y, batch_size=32, epochs=5)
# 保存整个模型
model.save('all_model.h5')
# 导入整个模型
model = tf.keras.models.load_model('all_model.h5')

6 将keras用于Estimator

Estimator API 用于针对分布式环境训练模型。它适用于一些行业使用场景，例如用大型数据集进行分布式训练并导出模型以用于生产

model = tf.keras.Sequential([layers.Dense(10,activation='softmax'),
                          layers.Dense(10,activation='softmax')])

model.compile(optimizer=tf.keras.optimizers.RMSprop(0.001),
              loss='categorical_crossentropy',
              metrics=['accuracy'])

estimator = tf.keras.estimator.model_to_estimator(model)

7 Eager execution

Eager execution是一个动态执行的编程环境，它可以立即评估操作。Keras不需要此功能，但它受tf.keras程序支持和对检查程序和调试有用。

所有的tf.keras模型构建API都与Eager execution兼容。尽管可以使用Sequential和函数API，但Eager execution有利于模型子类化和构建自定义层：其要求以代码形式编写前向传递的API（而不是通过组装现有层来创建模型的API）。

8 多GPU上运行

tf.keras模型可使用tf.distribute.Strategy在多个GPU上运行 。该API在多个GPU上提供了分布式培训，几乎无需更改现有代码。

当前tf.distribute.MirroredStrategy是唯一受支持的分发策略。MirroredStrategy在单台计算机上使用全缩减进行同步训练来进行图内复制。要使用 distribute.Strategys，请将优化器实例化以及模型构建和编译嵌套在Strategys中.scope()，然后训练模型。

以下示例tf.keras.Model在单个计算机上的多GPU分配。

首先，在分布式策略范围内定义一个模型：

strategy = tf.distribute.MirroredStrategy()
with strategy.scope():
    model = tf.keras.Sequential()
    model.add(layers.Dense(16, activation='relu', input_shape=(10,)))
    model.add(layers.Dense(1, activation='sigmoid'))
    optimizer = tf.keras.optimizers.SGD(0.2)
    model.compile(loss='binary_crossentropy', optimizer=optimizer)
model.summary()

然后像单gpu一样在数据上训练模型即可

x = np.random.random((1024, 10))
y = np.random.randint(2, size=(1024, 1))
x = tf.cast(x, tf.float32)
dataset = tf.data.Dataset.from_tensor_slices((x, y))
dataset = dataset.shuffle(buffer_size=1024).batch(32)
model.fit(dataset, epochs=1)

# define some hyper parameters
batch_size = 100 
n_inputs = 784
n_classes = 10 
n_epochs = 100 

# get the data
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

# reshape the two dimensional 28 x 28 pixels
# sized images into a single vector of 784 pixels
x_train = x_train.reshape(60000, n_inputs)
x_test = x_test.reshape(10000, n_inputs)

# convert the input values to float32
x_train = x_train.astype(np.float32)
x_test = x_test.astype(np.float32)

# normalize the values of image vectors to fit under 1
x_train /= 255
x_test /= 255

# convert output data into one hot encoded format
y_train = tf.keras.utils.to_categorical(y_train, n_classes)
y_test = tf.keras.utils.to_categorical(y_test, n_classes)

# build a sequential model
model = tf.keras.Sequential()
# the first layer has to specify the dimensions of the input vector
model.add(layers.Dense(units=128, activation='sigmoid', input_shape=(n_inputs,)))
# add dropout layer for preventing overfitting
model.add(layers.Dropout(0.1))
model.add(layers.Dense(units=128, activation='sigmoid'))
model.add(layers.Dropout(0.1))
# output layer can only have the neurons equal to the number of outputs
model.add(layers.Dense(units=n_classes, activation='softmax'))

# print the summary of our model
model.summary()

# compile the model
model.compile(loss='categorical_crossentropy',
              optimizer=tf.keras.optimizers.SGD(),
              metrics=['accuracy'])

# train the model
model.fit(x_train, y_train,
          batch_size=batch_size,
          epochs=n_epochs)

# evaluate the model and print the accuracy score
scores = model.evaluate(x_test, y_test)

print('\n loss:', scores[0])
print('\n accuracy:', scores[1])