【优化求解】基于混合正弦余弦算法和Lévy飞行改进麻雀算法求解最优目标matlab源码

1 模型

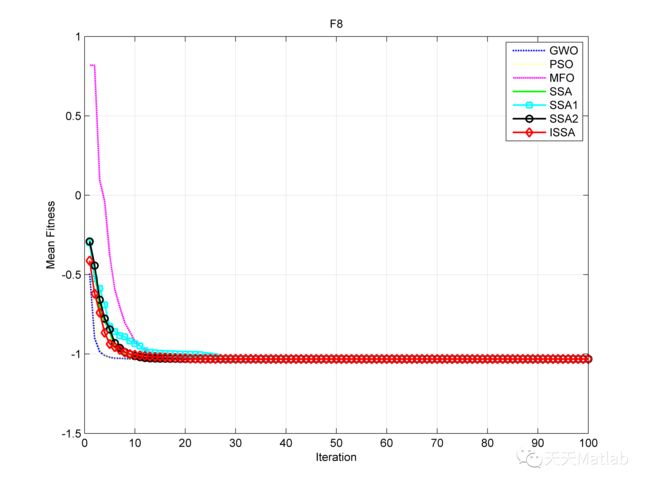
针对基本麻雀搜索算法抗局部最优能力弱的问题，提出了一种混合正弦余弦算法和 Lévy 飞行的麻雀算法（ISSA）。首先，在发现者位置更新方式中融合正弦余弦算法思想并引入非线性动态学习因子，平衡局部和全局的开掘能力，并加快收敛速度；然后，在跟随者位置更新方式中引进 Lévy 飞行策略，对当前最优解进行扰动变异，加强局部逃逸能力；最后，基于 8 个基准测试函数进行性能测验，结果表明 ISSA 与其余四种算法相比，寻优精度至少提升了 49 个数量级，求解效率得到较大提升。

2 部分代码

%% 清除环境变量

clear 

clc

%% 参数设置

N = 30;             % 种群规模

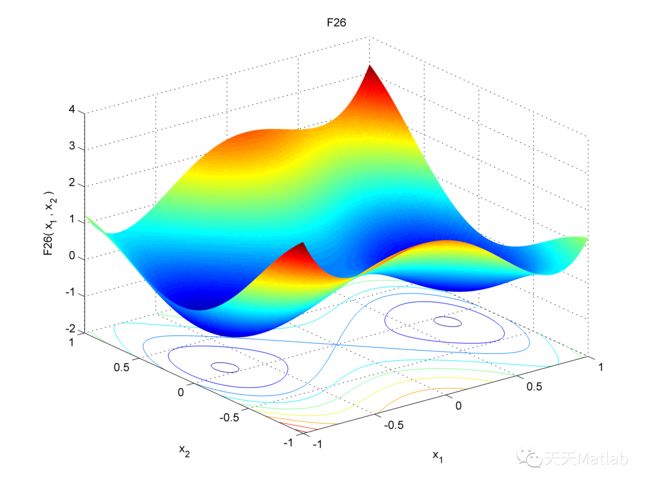
Function_name = 'F26';         % 从F1到F23的测试函数的名称（本文中的表1、2、3）

Max_iteration = 100;           % 最大迭代次数

cnt_max = 30;

% 加载所选基准函数的详细信息

[lb, ub, dim, fobj] = Get_Functions_details(Function_name);

Curve_GWO = zeros(1, Max_iteration);

Curve_PSO = zeros(1, Max_iteration);

Curve_MFO = zeros(1, Max_iteration);

Curve_SSA = zeros(1, Max_iteration);

Curve_SSA1 = zeros(1, Max_iteration);

Curve_SSA2 = zeros(1, Max_iteration);

Curve_ISSA = zeros(1, Max_iteration);

for cnt = 1:cnt_max

    disp(['第', num2str(cnt), '次迭代']);

    % 初始化种群位置

    X = initialization(N, dim, ub, lb);

    

    [GWO_Best_score(cnt), GWO_Best_pos(cnt, :), GWO_Curve] = GWO(X, N, Max_iteration, lb, ub, dim, fobj);

    [PSO_Best_score(cnt), PSO_Best_pos(cnt, :), PSO_Curve] = PSO(X, N, Max_iteration, lb, ub, dim, fobj);

    [MFO_Best_score(cnt), MFO_Best_pos(cnt, :), MFO_Curve] = MFO(X, N, Max_iteration, lb, ub, dim, fobj);

    [SSA_Best_score(cnt), SSA_Best_pos(cnt, :), SSA_Curve] = SSA(X, N, Max_iteration, lb, ub, dim, fobj);

    [SSA1_Best_score(cnt), SSA1_Best_pos(cnt, :), SSA1_Curve] = SSA1(X, N, Max_iteration, lb, ub, dim, fobj);

    [SSA2_Best_score(cnt), SSA2_Best_pos(cnt, :), SSA2_Curve] = SSA2(X, N, Max_iteration, lb, ub, dim, fobj);

    [ISSA_Best_score(cnt), ISSA_Best_pos(cnt, :), ISSA_Curve] = ISSA(X, N, Max_iteration, lb, ub, dim, fobj);

    

    Curve_GWO = Curve_GWO+GWO_Curve;

    Curve_PSO = Curve_PSO+PSO_Curve;

    Curve_MFO = Curve_MFO+MFO_Curve;

    Curve_SSA = Curve_SSA+SSA_Curve;

    Curve_SSA1 = Curve_SSA1+SSA1_Curve;

    Curve_SSA2 = Curve_SSA2+SSA2_Curve;

    Curve_ISSA = Curve_ISSA+ISSA_Curve;

end

Curve_GWO = Curve_GWO/cnt_max;

Curve_PSO = Curve_PSO/cnt_max;

Curve_MFO = Curve_MFO/cnt_max;

Curve_SSA = Curve_SSA/cnt_max;

Curve_SSA1 = Curve_SSA1/cnt_max;

Curve_SSA2 = Curve_SSA2/cnt_max;

Curve_ISSA = Curve_ISSA/cnt_max;

std_GWO = std(GWO_Best_score);

std_PSO = std(PSO_Best_score);

std_MFO = std(MFO_Best_score);

std_SSA = std(SSA_Best_score);

std_SSA1 = std(SSA1_Best_score);

std_SSA2 = std(SSA2_Best_score);

std_ISSA = std(ISSA_Best_score);

best_GWO = max(GWO_Best_score);

best_PSO = max(PSO_Best_score);

best_MFO = max(MFO_Best_score);

best_SSA = max(SSA_Best_score);

best_SSA1 = max(SSA1_Best_score);

best_SSA2 = max(SSA2_Best_score);

best_ISSA = max(ISSA_Best_score);

worst_GWO = min(GWO_Best_score);

worst_PSO = min(PSO_Best_score);

worst_MFO = min(MFO_Best_score);

worst_SSA = min(SSA_Best_score);

worst_SSA1 = min(SSA1_Best_score);

worst_SSA2 = min(SSA2_Best_score);

worst_ISSA = min(ISSA_Best_score);

mean_GWO = mean(GWO_Best_score);

mean_PSO = mean(PSO_Best_score);

mean_MFO = mean(MFO_Best_score);

mean_SSA = mean(SSA_Best_score);

mean_SSA1 = mean(SSA1_Best_score);

mean_SSA2 = mean(SSA2_Best_score);

mean_ISSA = mean(ISSA_Best_score);

%% 画图

% 1、画出所选基准函数的三维立体图形

figure;

func_plot(Function_name);

title(Function_name)

xlabel('x_1');

ylabel('x_2');

zlabel([Function_name,'( x_1 , x_2 )'])

img =gcf;  %获取当前画图的句柄

print(img, '-dpng', '-r600', './img1.png') 

% 2、画出目标函数值变化曲线图

figure;

t = 1:Max_iteration;

plot(t, Curve_GWO, 'b-.', t, Curve_PSO, 'y:', t, Curve_MFO, 'm--', t, Curve_SSA, 'g', ...

    t, Curve_SSA1, 'cs-', t, Curve_SSA2, 'ko-', t, Curve_ISSA, 'rd-', 'linewidth', 1.5);

title('F8')

xlabel('Iteration');

ylabel('Mean Fitness');

axis fill

grid on

box on

legend('GWO', 'PSO', 'MFO', 'SSA', 'SSA1', 'SSA2', 'ISSA');

img =gcf;  %获取当前画图的句柄

print(img, '-dpng', '-r600', './img.png')         %即可得到对应格式和期望dpi的图像

%% 显示结果

disp(['函数：', num2str(Function_name)]);

disp(['GWO：最大值: ', num2str(best_GWO), ',最小值:', num2str(worst_GWO), ',平均值:', num2str(mean_GWO), ',标准差:', num2str(std_GWO)]);

disp(['PSO：最大值: ', num2str(best_PSO), ',最小值:', num2str(worst_PSO), ',平均值:', num2str(mean_PSO), ',标准差:', num2str(std_PSO)]);

disp(['MFO：最大值: ', num2str(best_MFO), ',最小值:', num2str(worst_MFO), ',平均值:', num2str(mean_MFO), ',标准差:', num2str(std_MFO)]);

disp(['SSA：最大值: ', num2str(best_SSA), ',最小值:', num2str(worst_SSA), ',平均值:', num2str(mean_SSA), ',标准差:', num2str(std_SSA)]);

disp(['SSA1：最大值: ', num2str(best_SSA1), ',最小值:', num2str(worst_SSA1), ',平均值:', num2str(mean_SSA1), ',标准差:', num2str(std_SSA1)]);

disp(['SSA2：最大值: ', num2str(best_SSA2), ',最小值:', num2str(worst_SSA2), ',平均值:', num2str(mean_SSA2), ',标准差:', num2str(std_SSA2)]);

disp(['ISSA：最大值: ', num2str(best_ISSA), ',最小值:', num2str(worst_ISSA), ',平均值:', num2str(mean_ISSA), ',标准差:', num2str(std_ISSA)]);

3 仿真结果

4 参考文献

[1]田慕玲, 杨宇博, 许春雨,等. 一种基于混沌麻雀搜索算法的煤岩分界图像增强方法:.