统计学习方法（二） K近邻（KNN）

第一节的感知机使用了一种做辅助超平面的方式来分类，K近邻也可以分类（可以回归，但不讨论），而且从数学思想上更加直观：简单来说就是预测样本距离哪个类别最近就分为哪一类。相比感知机，K近邻天然具有多分类的能力。另外，K近邻没有明显的“学习”过程。算法最主要的是如何设置距离的度量和分类决策规则。（说白了就是怎么算距离，算好了又怎么确定类别）

原书中对于K近邻是这样说的：

K近邻法的输入为示例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。K近邻罚假设给定一个训练数据集，其中的实例类别已定。分类时对新的实例，根据其k个最近邻的训练实例的类别，通过多数表决等方式进行预测。…… k值的选择、距离度量及分类决策规则是K近邻法的三个基本要素。

关于距离度量可以参考这里

K近邻算法

1. 根据给定的距离度量，在训练集$T$中找出与$x$最邻近的$k$个点，涵盖这$k$个点的$x$的邻域记做$N_k(x)$；

2. 在$N_k(x)$中根据分类决策规则（如多数表决）决定$x$的类别$y$；

$y={\mathrm{argmax}}_{c_j}{\sum }_{x_i\in N_k(x)}I(y_i=c_i),i=1,2,...,N,j=1,2,...K$

$I$为指示函数，即当$y_i=c_i$时$I$为1，否则$I$为0.

找到前$k$个距离最近的点后，使用多数表决（就是看哪个类别的点多）确定类别。

K近邻的特殊情况是$k=1$的情形，称为最近邻算法。对于输入的实例点，最近邻法将训练数据集中与实例点最近邻的类作为实例点的类。通常$k$会选取一个较小的数，但不是1.因为如果$k$较大，则实际距离较远的点会影响结果，容易产生过拟合；但$k$选1时，又容易收到噪音点的影响。

KD树

在样本数量很大，维度较高的情况下，K近邻是非常耗费算力的，因为要逐一计算每个高维向量的距离。KD树的一个减少距离计算的方法。

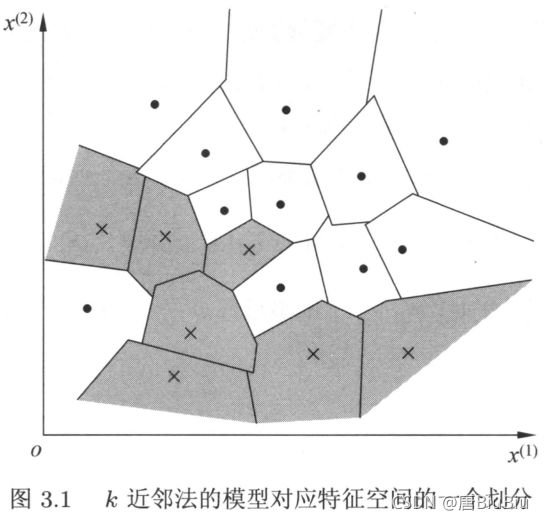
简单来说就是把样本空间划分为多个超空间，每个超空间都对应一个可能的类。这样的话只需要每个预测样本落在哪个超空间内就可以分类，分类的方法使用决策树算法。今天没有做KD树的实现，这里挖个坑，以后补上。

K近邻代码

import os
import time
import cv2
import numpy as np
from collections import Counter
import Distance


def loaddata(jpgpath):
    print('read data...')
    itemlist = os.listdir(jpgpath)
    item = []
    label = []

    for i in itemlist:
        img = cv2.imread(f"{
       jpgpath}/{
       i}",0).reshape(28*28,-1).T
        item.append(img)
        label.append(i.split('.')[0][-1])
    print('finshed')
    return item,label


def getclosest(x,data,label,k=30):
    '''
    预测样本x的类别
    '''
    m = len(data)
    dist=[]
    for i in range(m):
        dist.append(Distance.mks_distance(data[i][0],x[0],p=1))
    dist,label = zip(*sorted(zip(dist,label)))
    closest = Counter(label[0:k])
    closest = closest.most_common(1)[0][0]
    return closest


def test(data1,label1,data2,label2):
    '''
    测试正确率
    '''
    m = len(data1)
    result = 0
    for i in range(m):
        pred_y = getclosest(data1[i],data2,label2)
        if pred_y == label1[i]:
            result += 1
        print(f'item:{
       i}/{
       m}')
    return result/m




if __name__ == '__main__':
    start = time.time()

    item,label = loaddata('./train_images')
    test_item,test_label = loaddata('./test_images')
    print(test(test_item,test_label,item,label))

    end = time.time()
    print(f'总计使用时间：{
       end-start}')