MATLAB数学建模:常用建模函数
常用建模函数
本文将对常用于 MATLAB 建模的函数,如曲线拟合函数、参数估计函数、插值函数等,作详细介绍。
文章目录
- 常用建模函数
-
- 1. 曲线拟合函数
-
- 1.1 多项式拟合
- 1.2 加权最小方差拟合
- 1.3 非线性曲线拟合
- 2. 参数估计函数
-
- 2.1 点估计
-
- 2.1.1 最大似然法
- 2.1.2 矩法
- 2.2 区间估计
- 3. 插值函数
-
- 3.1 一维插值
- 3.2 二维插值
- 3.3 样条插值
1. 曲线拟合函数
曲线拟合函数的主要功能是寻找一条可最好地表现有噪声的测量数据的平滑曲线,从这些测量数据中寻求两个函数变量间的关系或变化趋势,最终得到曲线拟合的函数表达式: y = f ( x ) . y = f(x). y=f(x).
一般情况下,MATLAB 的曲线拟合方法是采用“最小方差”函数,其中方差是拟合曲线与已知数据之间的垂直距离值。
1.1 多项式拟合
在 MATLAB 中,我们采用函数 polyfit()对给定的数据进行多项式拟合,得到该多项式的系数。
1. polyfit(x,y,n)
2. [p,E] = polyfit(x,y,n)
- 找到次数为 n n n 的最优拟合多项式系数。
- 返回最有拟合多项式 p p p 和矩阵 E E E:多项式系数在向量 p p p 中,矩阵 E E E 用在
polyval函数中计算误差。
注:使用函数 polyfit()进行拟合时,多项式次数最大不得超过 l e n g t h ( x ) − 1 length(x)-1 length(x)−1.
1.2 加权最小方差拟合
加权最小方差 (WLS) 指根据基础数据本身各自准确度的不同,在拟合时为每个数据赋以不同的加权数值。该方法比单纯的最小方差法要更加符合“多项式拟合”的要求。
对应 N N N 阶多项式的拟合公式,要求解拟合系数,就要求解线性方程组:其系数矩阵和所需要求解的拟合系数矩阵分别为:
A = [ x 1 N ⋯ x 1 ⋯ 1 x 2 N ⋯ x 2 ⋯ 1 ⋮ ⋯ ⋮ x m N ⋯ x m ⋯ 1 ] A = \begin{bmatrix} x_{1}^{N} & \cdots & x^{1} \cdots & 1 \\ x_{2}^{N} & \cdots & x^{2} \cdots & 1 \\ \vdots & \cdots & \vdots \\ x_{m}^{N} & \cdots & x^{m} \cdots & 1 \\ \end{bmatrix} A=⎣⎢⎢⎢⎡x1Nx2N⋮xmN⋯⋯⋯⋯x1⋯x2⋯⋮xm⋯111⎦⎥⎥⎥⎤
θ = [ θ n θ n − 1 ⋮ θ 1 ] \theta = \begin{bmatrix}\theta_{n}\\ \theta_{n-1}\\ \vdots \\ \theta_{1}\end{bmatrix} θ=⎣⎢⎢⎢⎡θnθn−1⋮θ1⎦⎥⎥⎥⎤
使用加权最小方差方法求解所得的拟合系数是:
θ m n = [ θ m n n θ m n = 1 n ⋮ θ 1 n ] = [ A T M A ] − 1 A T M y . \theta^{n}_{m} = \begin{bmatrix}\theta^{n}_{mn}\\ \theta^{n}_{mn=1}\\ \vdots \\ \theta_{1}^{n}\end{bmatrix} = [A^{T}MA]^{-1}A^{T}My. θmn=⎣⎢⎢⎢⎡θmnnθmn=1n⋮θ1n⎦⎥⎥⎥⎤=[ATMA]−1ATMy.
其对应的加权最小方差为:
J m = [ A θ − y ] T W [ A θ − y ] J_{m} = [A\theta-y]^{T}W[A\theta - y] Jm=[Aθ−y]TW[Aθ−y]
1.3 非线性曲线拟合
2. 参数估计函数
参数估计包括 点估计 和 区间估计.
2.1 点估计
点估计是使用单个数值作为参数的一种估计方式。点估计在抽样推断中 不考虑抽样误差 ,直接以抽样指标代替全体指标。因为个别样本的抽样指标不等于全体指标,因此用抽样指标直接代替全体指标不可避免的会有误差。目前使用较多的点估计方法是最大似然法和矩法。
2.1.1 最大似然法
最大似然法是在待估参数的可能取值范围内,挑选使似然函数值最大的参数值作为最大似然估计量。
最大似然估计法得到的估计量通常不仅仅满足无偏性、有效性等基本条件,还能保证其为充分统计量,因此一般建议在点估计和区间估计中使用最大似然法。
M A T L A B MATLAB MATLAB 使用函数 m l e mle mle 进行最大似然估计:
phat = mle('dist',data)
使用 d a t a data data 向量中的样本数据,返回 d i s t dist dist 指定的分布的最大似然估计。
2.1.2 矩法
矩估计,就是利用样本矩来估计总体中相应的参数的方法。我们首先推导涉及感兴趣的参数的总体矩(即所考虑的随机变量的幂的期望值)的方程。然后取出一个样本并从这个样本估计总体矩。接着使用样本矩取代(未知的)总体矩,解出感兴趣的参数。从而得到那些参数的估计。
待估参数通常作为总体原点矩或原点矩的函数,此时可以用该总体样本的原点矩或样本原点矩的函数值作为待估参数的估计,称这种方法为矩法。
例如:样本均值总是总体均值的矩估计量、样本方差是总体方差的矩估计量,样本标准差是总体标准差的矩估计量。
M A T L A B MATLAB MATLAB 中计算矩的函数为 moment(X,order).
2.2 区间估计
区间估计是在点估计的基础上,通过给出总体参数估计的一个区间范围(该区间通常由样本统计量加减估计误差得到)从而减少误差的估计方法。
求参数的区间估计,首先需要求出该参数的点估计,随后构造一个含有该参数的随机量,并根据一定的置信水平求该估计值的范围。
在 M A T L A B MATLAB MATLAB 中使用 mle函数进行最大似然估计时,有如下几种调用格式:
1. [phat,pci] = mle('dist',data)
2. [phat,pci] = mle('dist',data,alpha)
3. [phat,pci] = mle('dist',data,alpha,p1)
- 返回最大似然估计和 95 % 95\% 95% 置信区间。
- 返回指定分布的最大似然估计值和 100 ( 1 − a l p h a ) % 100(1-alpha)\% 100(1−alpha)% 置信区间。
- 该形式只用于二项分布,其中 p 1 p1 p1 为试验次数。
3. 插值函数
插值函数的作用是在给定基准数据的前提下,平滑地估算出基准数据之间其他点的函数值。当获取其他点上函数值的代价高昂时,插值就会起到较大的作用。在数字信号处理和图像处理中,插值是一种常用方法。 MATLAB 提供了大量插值函数。下面,对一些常用插值函数进行介绍:
3.1 一维插值
一维插值就是对单值函数 y = f ( x ) y = f(x) y=f(x) 进行插值。在 MATLAB 中,一维插值有基于多项式插值和基于快速 Fourier 变换的插值两种类型。
在 MATLAB 中,我们使用函数 interpl()实现一维多项式插值。该函数使用多项式插值法,利用多项式函数,通过所提供的数据点计算目标插值点上的插值函数值。其调用格式如下:
1. yi = interpl(x,Y,xi)
2. yi = interpl(Y,xi)
3. yi = interpl(Y,xi,method)
- 参量 x x x 指定数据 Y Y Y 的点,若 Y Y Y 为一个矩阵,则按照 Y Y Y 的每列计算。 y i yi yi 是阶数为 l e n g t h ( x i ) ∗ s i z e ( Y , 2 ) length(xi) * size(Y,2) length(xi)∗size(Y,2) 的输出矩阵。
函数返回插值向量 y i yi yi:其每一个元素对应于参量 x i xi xi。- 默认 x = 1 : N x = 1:N x=1:N ( N N N 为向量 Y Y Y 的长度,或为矩阵 Y Y Y 的行数。)
- 指定计算差值的特定算法
method:
可以选用的算法如下:
- 临近点插值:
method = 'nearest' - 线性插值:
method = 'linear' - 三次样条插值:
method = 'spline' - 分段三次Hermite插值:
method = 'pchip' - 三次多项式插值:
method = 'cubic'
[例]
已知当 x = 0 : 0.3 : 3 x = 0:0.3:3 x=0:0.3:3 时,函数 y = ( x 2 − 4 x + 2 ) s i n ( x ) y = (x^{2}-4x+2)sin(x) y=(x2−4x+2)sin(x) 的值,对 x i = 0 : 0.01 : 3 xi = 0:0.01:3 xi=0:0.01:3 采用不同方法进行插值处理。
clc;clear all;
x = 0:0.3:3;
y = (x.^2 - 4*x + 2).*sin(x);
xi = 0:0.01:3;
yi_nearest = interp1(x,y,xi,'nearest');
yi_linear = interp1(x,y,xi);
yi_spline = interp1(x,y,xi,'spline');
yi_pchip = interp1(x,y,xi,'pchip');
yi_v5cubic = interp1(x,y,xi,'v5cubic');
%绘图
figure;
hold on;
subplot(231);
plot(x,y,'ro');
title('已知数据点');
subplot(232);
plot(x,y,'ro',xi,yi_nearest,'b- ');
title('临近点插值');
subplot(233);
plot(x,y,'ro',xi,yi_linear,'b- ');
title('线性插值');
subplot(234);
plot(x,y,'ro',xi,yi_spline,'b- ');
title('三次样条插值');
subplot(235);
plot(x,y,'ro',xi,yi_pchip,'b- ');
title('分段三次Hermite插值');
subplot(236);
plot(x,y,'ro',xi,yi_v5cubic,'b- ');
title('三次多项式插值');
3.2 二维插值
二维插值主要用于图像处理和数据可视化,其基本思想与一维插值相同。在 MATLAB中,使用函数 interp2()进行二维插值。调用格式如下:
1. Zi = interp2(X,Y,Z,Xi,Yi)
2. Zi = interp2(Z,Xi,Yi)
3. Zi = interp2(Z,n)
4. Zi = interp2(X,Y,Z,Xi,Yi,method)
- 返回矩阵 Z i Zi Zi,其元素包含对应于参量 X i Xi Xi 和 Y i Yi Yi 的元素,即: Z i ( i , j ) ∈ [ X i ( i , j ) , Y i ( i , j ) ] . Zi(i,j) \in [Xi(i,j),Yi(i,j)]. Zi(i,j)∈[Xi(i,j),Yi(i,j)].
- 默认 X = 1 : n , Y = 1 : m X = 1:n, \ Y = 1:m X=1:n, Y=1:m,其中 [ m , n ] = s i z e ( Z ) . [m,n] = size(Z). [m,n]=size(Z).
- 作 n n n 次递归计算,在 Z Z Z 的每两个元素之间插入它们的二维插值,这样 Z Z Z 的阶数将不断增加。
- 用指定的算法计算二维插值。
可以选用的算法如下:
- 双线性插值:
method = 'linear' - 最邻近插值:
method = 'nearest' - 三次样条插值:
method = 'spline' - 双三次插值:
method = 'cubic'
[例]
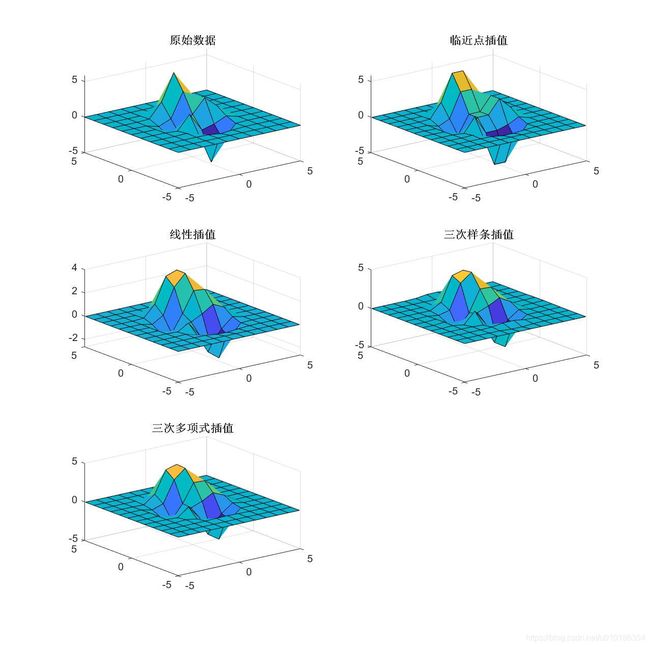
使用 meshgrid()函数生成原始数据和插值数据,并分别采用nearest,linear,spline和cubic方法进行二维插值,最终绘出三维表面图:
>> [x,y] = meshgrid(-5:1:5)
x =
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
y =
-5 -5 -5 -5 -5 -5 -5 -5 -5 -5 -5
-4 -4 -4 -4 -4 -4 -4 -4 -4 -4 -4
-3 -3 -3 -3 -3 -3 -3 -3 -3 -3 -3
-2 -2 -2 -2 -2 -2 -2 -2 -2 -2 -2
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1
2 2 2 2 2 2 2 2 2 2 2
3 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4 4 4 4 4 4
5 5 5 5 5 5 5 5 5 5 5
>> [xi,yi] = meshgrid(-5:0.9:5)
xi =
Columns 1 through 10
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
-5.0000 -4.1000 -3.2000 -2.3000 -1.4000 -0.5000 0.4000 1.3000 2.2000 3.1000
Columns 11 through 12
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
4.0000 4.9000
yi =
Columns 1 through 10
-5.0000 -5.0000 -5.0000 -5.0000 -5.0000 -5.0000 -5.0000 -5.0000 -5.0000 -5.0000
-4.1000 -4.1000 -4.1000 -4.1000 -4.1000 -4.1000 -4.1000 -4.1000 -4.1000 -4.1000
-3.2000 -3.2000 -3.2000 -3.2000 -3.2000 -3.2000 -3.2000 -3.2000 -3.2000 -3.2000
-2.3000 -2.3000 -2.3000 -2.3000 -2.3000 -2.3000 -2.3000 -2.3000 -2.3000 -2.3000
-1.4000 -1.4000 -1.4000 -1.4000 -1.4000 -1.4000 -1.4000 -1.4000 -1.4000 -1.4000
-0.5000 -0.5000 -0.5000 -0.5000 -0.5000 -0.5000 -0.5000 -0.5000 -0.5000 -0.5000
0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000
1.3000 1.3000 1.3000 1.3000 1.3000 1.3000 1.3000 1.3000 1.3000 1.3000
2.2000 2.2000 2.2000 2.2000 2.2000 2.2000 2.2000 2.2000 2.2000 2.2000
3.1000 3.1000 3.1000 3.1000 3.1000 3.1000 3.1000 3.1000 3.1000 3.1000
4.0000 4.0000 4.0000 4.0000 4.0000 4.0000 4.0000 4.0000 4.0000 4.0000
4.9000 4.9000 4.9000 4.9000 4.9000 4.9000 4.9000 4.9000 4.9000 4.9000
Columns 11 through 12
-5.0000 -5.0000
-4.1000 -4.1000
-3.2000 -3.2000
-2.3000 -2.3000
-1.4000 -1.4000
-0.5000 -0.5000
0.4000 0.4000
1.3000 1.3000
2.2000 2.2000
3.1000 3.1000
4.0000 4.0000
4.9000 4.9000
>> z = peaks(x,y);
>> zi_nearest = interp2(x,y,z,xi,yi,'nearest')
zi_nearest =
Columns 1 through 9
0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000
0.0000 0.0000 0.0000 0.0000 0.0001 -0.0008 -0.0008 -0.0004 -0.0000
0.0000 0.0000 0.0001 0.0034 -0.0299 -0.2450 -0.2450 -0.1100 -0.0043
-0.0000 0.0000 0.0007 0.0468 -0.5921 -4.7596 -4.7596 -2.1024 -0.0616
-0.0000 -0.0000 -0.0088 -0.1301 1.8559 -0.7239 -0.7239 -0.2729 0.4996
-0.0000 -0.0001 -0.0365 -1.3327 -1.6523 0.9810 0.9810 2.9369 1.4122
-0.0000 -0.0001 -0.0365 -1.3327 -1.6523 0.9810 0.9810 2.9369 1.4122
-0.0000 -0.0000 -0.0137 -0.4808 0.2289 3.6886 3.6886 2.4338 0.5805
-0.0000 -0.0000 0.0000 0.0797 2.0967 5.8591 5.8591 2.2099 0.1328
-0.0000 0.0000 0.0000 0.0053 0.1099 0.2999 0.2999 0.1107 0.0057
0.0000 0.0000 0.0000 0.0000 0.0004 0.0012 0.0012 0.0004 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
Columns 10 through 12
0.0000 0.0000 0.0000
0.0000 0.0000 0.0000
-0.0000 0.0000 0.0000
0.0004 0.0000 0.0000
0.0130 0.0000 0.0000
0.0331 0.0001 0.0000
0.0331 0.0001 0.0000
0.0125 0.0000 0.0000
0.0013 0.0000 0.0000
0.0000 0.0000 0.0000
0.0000 0.0000 0.0000
0.0000 0.0000 0.0000
>> zi_linear = interp2(x,y,z,xi,yi)
zi_linear =
Columns 1 through 9
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000
0.0000 0.0000 0.0000 0.0000 0.0001 -0.0003 -0.0006 -0.0003 -0.0000
0.0000 0.0000 0.0000 0.0019 -0.0132 -0.1100 -0.1529 -0.0627 -0.0028
-0.0000 0.0000 0.0004 0.0238 -0.2406 -1.9143 -2.6450 -1.0666 -0.0355
-0.0000 -0.0000 -0.0040 -0.0430 0.5023 -0.7308 -1.8048 -0.6207 0.2217
-0.0000 -0.0001 -0.0181 -0.5188 -0.2315 0.1152 0.6099 1.2192 0.7693
-0.0000 -0.0001 -0.0219 -0.7026 -0.9367 0.5821 2.3327 2.2388 0.8686
-0.0000 -0.0000 -0.0077 -0.2217 0.3485 2.5645 3.5505 1.7905 0.3588
-0.0000 -0.0000 0.0000 0.0454 1.0455 3.2233 3.5644 1.2853 0.0861
-0.0000 0.0000 0.0000 0.0034 0.0613 0.1845 0.2019 0.0713 0.0041
0.0000 0.0000 0.0000 0.0000 0.0003 0.0008 0.0009 0.0003 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0001 0.0000 0.0000
Columns 10 through 12
0.0000 0.0000 0.0000
0.0000 0.0000 0.0000
-0.0000 0.0000 0.0000
0.0003 0.0000 0.0000
0.0072 0.0000 0.0000
0.0208 0.0001 0.0000
0.0224 0.0001 0.0000
0.0082 0.0000 0.0000
0.0010 0.0000 0.0000
0.0000 0.0000 0.0000
0.0000 0.0000 0.0000
0.0000 0.0000 0.0000
>> zi_spline = interp2(x,y,z,xi,yi,'spline')
zi_spline =
Columns 1 through 9
0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000
0.0000 0.0001 -0.0002 0.0006 -0.0147 -0.1183 -0.1423 -0.0363 -0.0008
-0.0000 -0.0003 0.0009 -0.0023 0.0489 0.2536 0.2794 0.0681 0.0032
0.0000 -0.0010 0.0032 -0.0050 -0.1001 -2.6601 -3.5435 -0.9322 0.0056
-0.0000 -0.0179 0.0511 -0.1802 1.2994 -0.7065 -2.9008 -0.7885 0.2243
-0.0000 -0.0342 0.0842 -0.7251 -0.2234 0.3610 0.9281 1.6709 0.8407
-0.0000 -0.0252 0.0542 -0.7538 -1.8391 -0.0994 2.7080 2.6268 0.8564
-0.0000 -0.0081 0.0195 -0.1771 0.1687 3.3755 4.4578 1.5058 0.2067
-0.0000 -0.0035 0.0106 -0.0097 0.7717 3.9375 4.3151 0.9975 0.0185
-0.0000 0.0000 -0.0001 -0.0010 -0.0144 -0.0533 -0.0524 -0.0087 0.0010
0.0000 -0.0000 0.0000 -0.0000 0.0002 0.0009 0.0010 0.0002 0.0000
0.0000 -0.0002 0.0006 0.0006 0.0511 0.2412 0.2584 0.0563 -0.0002
Columns 10 through 12
-0.0000 0.0000 0.0000
-0.0002 -0.0000 0.0002
0.0004 0.0000 -0.0003
-0.0081 -0.0000 0.0079
-0.0195 0.0000 0.0240
-0.0238 0.0001 0.0450
-0.0133 0.0001 0.0360
0.0032 0.0000 0.0024
0.0064 0.0000 -0.0058
-0.0001 0.0000 0.0001
0.0000 0.0000 -0.0000
0.0004 -0.0000 -0.0004
>> zi_cubic = interp2(x,y,z,xi,yi,'cubic')
zi_cubic =
Columns 1 through 9
0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000
-0.0000 0.0000 0.0000 -0.0002 0.0002 0.0063 0.0089 0.0030 -0.0001
0.0000 -0.0000 0.0000 -0.0007 0.0016 0.0495 0.0702 0.0219 -0.0022
0.0000 -0.0001 -0.0020 0.0863 -0.1357 -2.4416 -3.3963 -1.1467 0.0299
-0.0000 0.0001 -0.0045 -0.0658 1.0047 -0.7197 -2.4363 -0.7968 0.2843
-0.0000 0.0010 0.0284 -0.6661 -0.2559 0.1535 0.7139 1.4907 0.8608
-0.0000 0.0013 0.0442 -0.8324 -1.5171 0.2944 2.7076 2.6324 0.8955
-0.0000 0.0004 0.0096 -0.2906 0.1871 2.9797 4.1520 1.7395 0.2194
0.0000 -0.0000 -0.0059 -0.0555 1.0063 3.8551 4.2442 1.1772 -0.0427
0.0000 -0.0000 -0.0001 -0.0000 0.0124 0.0426 0.0450 0.0111 -0.0011
0.0000 -0.0000 -0.0000 -0.0000 0.0002 0.0009 0.0010 0.0003 -0.0000
0.0000 0.0000 0.0000 0.0002 -0.0025 -0.0099 -0.0110 -0.0031 0.0001
Columns 10 through 12
0.0000 0.0000 -0.0000
-0.0000 -0.0000 -0.0000
-0.0000 -0.0000 0.0000
0.0030 -0.0000 0.0000
-0.0022 0.0000 -0.0003
-0.0177 0.0001 -0.0011
-0.0214 0.0001 -0.0012
-0.0086 0.0000 -0.0004
-0.0030 0.0000 -0.0000
-0.0000 -0.0000 0.0000
-0.0000 0.0000 -0.0000
0.0000 -0.0000 0.0000
>> figure;
>> hold on;
>> subplot(321);
>> surf(x,y,z);
>> title('原始数据');
>> subplot(322);
>> surf(xi,yi,zi_nearest);
>> title('临近点插值');
>> subplot(323);
>> surf(xi,yi,zi_linear);
>> title('线性插值');
>> subplot(324);
>> surf(xi,yi,zi_spline);
>> title('三次样条插值');
>> subplot(325);
>> surf(xi,yi,zi_cubic);
>> title('三次多项式插值');
>>
3.3 样条插值
在 MATLAB 中,使用函数 spline()进行三次样条插值。函数调用方法如下:
1. yy = spline(x,y,xx)
2. pp = spline(xy)
- 用三次样条插值计算出由向量 x , y x,y x,y 确定的一元函数 y = f ( x ) y = f(x) y=f(x) 在点 x x xx xx 处的值。若参量 y y y 是一个矩阵,则先以 y y y 的每一列和 x x x 配对,再分别计算由它们所确定的函数在点 x x xx xx 处的值,返回结果 y y yy yy 为一个阶数为 l e n g t h ( x x ) ∗ s i z e ( y , 2 ) length(xx)*size(y,2) length(xx)∗size(y,2) 的矩阵。
- 返回由向量 x , y x,y x,y 确定的,分段样条多项式的系数矩阵 p p pp pp,可用于
ppval,unmkpp的计算。
注:
对给定的,离散的测量数据 x , y x,y x,y ,要寻找一个三次多项式 y = p ( x ) y = p(x) y=p(x),以逼近每对数据点 ( x , y ) (x,y) (x,y) 间的曲线。显见通过一个点的三次多项式曲线条数无穷多。要使通过中间断点的三次多项式曲线具唯一性,就需要增加两个条件:
-
三次多项式在点 ( x i , y i ) (x_{i},y_{i}) (xi,yi) 和 ( x i + 1 , y i + 1 ) (x_{i+1},y_{i+1}) (xi+1,yi+1) 的一阶导数和二阶导数相等。
-
p ( x ) p(x) p(x) 在点 ( x i , y i ) (x_{i},y_{i}) (xi,yi) 处的斜率和曲率是连续的。
-
用三次样条插值计算出由向量 x , y x,y x,y 确定的一元函数 y = f ( x ) y = f(x) y=f(x) 在点 x x xx xx 处的值。若参量 y y y 是一个矩阵,则先以 y y y 的每一列和 x x x 配对,再分别计算由它们所确定的函数在点 x x xx xx 处的值,返回结果 y y yy yy 为一个阶数为 l e n g t h ( x x ) ∗ s i z e ( y , 2 ) length(xx)*size(y,2) length(xx)∗size(y,2) 的矩阵。
- 返回由向量 x , y x,y x,y 确定的,分段样条多项式的系数矩阵 p p pp pp,可用于
ppval,unmkpp的计算。
注:
对给定的,离散的测量数据 x , y x,y x,y ,要寻找一个三次多项式 y = p ( x ) y = p(x) y=p(x),以逼近每对数据点 ( x , y ) (x,y) (x,y) 间的曲线。显见通过一个点的三次多项式曲线条数无穷多。要使通过中间断点的三次多项式曲线具唯一性,就需要增加两个条件:
- 三次多项式在点 ( x i , y i ) (x_{i},y_{i}) (xi,yi) 和 ( x i + 1 , y i + 1 ) (x_{i+1},y_{i+1}) (xi+1,yi+1) 的一阶导数和二阶导数相等。
- p ( x ) p(x) p(x) 在点 ( x i , y i ) (x_{i},y_{i}) (xi,yi) 处的斜率和曲率是连续的。