【opencv-python】霍夫圆变换
霍夫变换检测直线的原理是利用累加器找到最大的 ( ρ , θ ) (ρ,θ) (ρ,θ)数对，如文章所述。圆形的数学表达式为 ( x − x c e n t e r ) 2 + ( y − y c e n t e r ) 2 = r 2 (x-x_{center})^2+(y-y_{center})^2=r^2 (x−xcenter)2+(y−ycenter)2=r2，其中 （ x c e n t e r , y c e n t e r ） （x_{center},y_{center}） （xcenter,ycenter）为圆心坐标， r r r为圆的直径。因此可知一个圆需要 x c e n t e r , y c e n t e r , r x_{center},y_{center},r xcenter,ycenter,r三个参数确定，如果采用霍夫直线相同的原理，则需要围绕被探测点对全域点进行搜索，进而获取可能的圆心坐标，然后再通过圆心坐标计算该点相对应的半径，构成 ( x c e n t e r , y c e n t e r , r ) (x_{center},y_{center},r) (xcenter,ycenter,r)数对，再利用累加方法对下一些像素点进行相同处操作，最后看哪个数对位置中的累加出的数值最大，即代表过这一簇点的圆。但是这种操作的计算量过大，效率比较低。于是H.K.YUEN等大神提出了一种优化算法，利用边缘点的梯度法向为路径进行圆心点搜索，可以大大缩小圆心点搜索范围，提高效率。
在opencv-python中，我们使用函数cv2.HoughCircles函数来解决圆识别问题，函数说明如下图所示：
每个参数的含义如下图所示：
- image：8位待处理灰度图像；
- circles：输出被检测到的圆，以三元素浮点型向量表示 ( x , y , r a d i u s ) (x,y,radius) (x,y,radius)；
- method：探测方法。当前的实现是用的CV_HOUGH_GRADIENT方法；
- dp：累加器分辨率与图像分辨率的反比。例如，如果dp=1，累加器的分辨率与输入图像相同。如果dp=2，则累加器的宽度和高度为原来的一半；
- minDist：检测到的圆中心之间的最小距离。如果参数太小，除了一个真实的圆外，还可能错误地检测到多个相邻圆，如果太大可能会错过一些圆；
- param1：第一个特定参数。对于CV_HOUGH_GRADIENT方法，它是传递给Canny()边缘检测器的两个阈值中较高的阈值（较低的阈值小两倍）；
- param2：第二个特定参数。对于CV_HOUGH_GRADIENT方法，它是检测阶段圆心的累加器阈值。它越小，可能检测到的假圆越多（因为满足累加器上限的条件变多了）。与累加器最大数值结果代表的圆将被首先返回。
- minRadius：最小圆半径；
- maxRadius：最大圆半径。
基于上文所述，霍夫圆检测的效果进行测试，待处理原图如下图所示：
处理代码如下所示：
img = cv2.imread('singlecircle.jpg',0)
img = cv2.medianBlur(img,5)
cimg = cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)
circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,minDist=20,param1=50,param2=30,minRadius=0,maxRadius=0)
print('circles1:', circles)
circles = np.uint16(np.around(circles))
print('circles2:', circles)
for i in circles[0,:]:
# draw the outer circle
cv2.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2)
# draw the center of the circle
cv2.circle(cimg,(i[0],i[1]),2,(0,0,255),3)
运行结果如下：
此时我们发现程序显示了很多圆形，并非是我们想要的结果，此时我们调整霍夫变换函数的参数，调整“minDist=20”为“minDist=100”，之后程序的运行效果为：
肉眼可见效果明显好了很多。从函数功能定义来看，输出circle变量应该包含形如 ( x c e n t e r , y c e n t e r , r ) (x_{center},y_{center},r) (xcenter,ycenter,r)形式的数对，我们将circle变量内容打印出来，如下图所示：
此处，我们可以思考一下，为什么圆心坐标最后都是.5的形式呢？当然，我们也可以通过改变其他参数的形式去达到只识别一个圆的目的，比如我们将"param2=30"修改为"param2=100"效果如下：
对于多个圆，我们也可以通过cv2.HoughCircles()函数进行识别，被处理原图如下图所示：
程序运行结束后效果如下图所示：
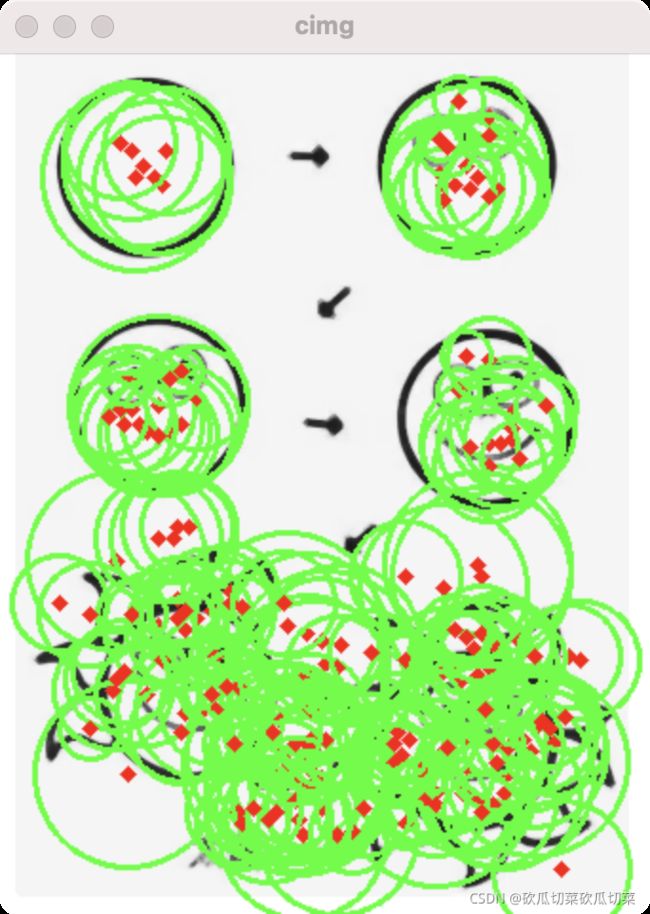
可见效果比较明显，但还没有达到比较规整的效果，通过调整函数中的参数可以实现我们想要的识别效果。在参数中，dp参数值得深入分析，其与累加器分辨率成反比，如果dp=1，累加器属正常状态，如果dp=2，则按照2倍执行累加，所以dp值越大，累加器累加速度越快，因此在上限阈值以上的被检测圆数量也就越多。为了测试，我们将dp调整为2，其他参数保持不变，观察函数的执行效果：
可见检测出来的圆多了好多。
欢迎大家在评论区留言评论，感谢大家的关注！