排序算法--冒泡排序、选择排序、稳定的选择排序、插入排序、折半插入排序原理介绍及代码示例
集合排序算法
冒泡排序
最简单的排序算法,它通过重复比较相邻元素,如果它们的顺序错误,则交换位置
由于其简单性,冒泡排序经常被用来引入排序算法的概念
优化点:如果内部循环没有引起任何交换,可以通过停止算法来优化。
//冒泡排序
public static void bubbleSort(int arr[]) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// swap arr[j+1] and arr[j]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
选择排序
选择排序
从未排序部分反复寻找最小元素(考虑升序),并将其放在数组的开头。该算法在给定数组中维护两个子数组。
- 已经排序的子数组。
- 剩余未排序的子数组。
在选择排序的每次迭代中,从未排序的子数组中选取最小元素(考虑升序)并移动到已排序的子数组中。
稳定的选择排序
通常实现的选择排序,针对值相同的元素,无法保证排序后,值相同的元素保持与排序前相同的顺序。
针对相同的值,为了保证其顺序与排序前一致,提供了稳定的选择排序算法。
如输入是 : 4A 5 3 2 4B 1
Output : 1 2 3 4A 4B 5, 即针对相同的值如4,排序后顺序与排序前一致(相对顺序)
//选择排序
public static void selectSort(int arr[]) {
int n = arr.length;
// One by one move boundary of unsorted subarray
for (int i = 0; i < n - 1; i++) {
// Find the minimum element in unsorted array
int min_idx = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
// Swap the found minimum element with the first element
if (min_idx != i) {
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
}
/**
* 排序后,针对相同的值,排序后的顺序与原来的顺序一致
* Input : 4A 5 3 2 4B 1
* Output : 1 2 3 4A 4B 5, 即针对相同的值,排序后顺序与排序前一致
*
* @param arr
*/
static void selectStableSort(int[] arr) {
int n = arr.length;
// Iterate through array elements
for (int i = 0; i < n - 1; i++) {
// Loop invariant : Elements till a[i - 1] are already sorted.
// Find minimum element from arr[i] to arr[n - 1].
int min = i;
for (int j = i + 1; j < n; j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
// Move minimum element at current i. 为了保证之前的顺序
int key = arr[min];
while (min > i) {
arr[min] = arr[min - 1];
min--;
}
arr[i] = key;
}
}
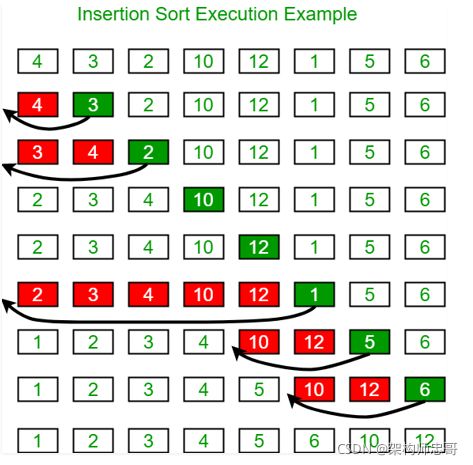
插入排序
经典的插入排序
插入排序是一种简单的排序算法,工作原理类似于对手中的扑克牌进行排序。数组实际上被分成了已排序部分和未排序部分。未排序部分的值被选中并放置在排序部分的正确位置。
算法:将大小为n的数组按升序排序:
折半插入排序
对插入排序算法的一种改进,由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度
折半插入排序算法是一种稳定的排序算法,比直接插入算法明显减少了关键字之间比较的次数,因此速度比直接插入排序算法快,但记录移动的次数没有变,所以折半插入排序算法的时间复杂度仍然为O(n^2),与直接插入排序算法相同。附加空间O(1)。
public static void insertSort(int arr[]) {
int n = arr.length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
//折半插入排序
public static int[] binaryInsertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
// arr[i]需要向前移动
if (arr[i] < arr[i - 1]) {
// 临时变量,存储当前下标的值
int temp = arr[i];
int j = i - 1;
// 从下标为0开始
int low = 0;
// 前一个值结束
int high = i - 1;
// 折半查找,有效的减少后续比较次数,循环结束后,high的值 +1 就是temp要插入的位置
while (low <= high) {
int mid = (low + high) / 2;
if (temp < arr[mid]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
// 从j(i-1)开始,往后移动,直到high +1,也就是要插入的位置
// 比temp(arr[i])大的值向后移动一位
for (; j >= high + 1; j--) {
arr[j + 1] = arr[j];
}
arr[high + 1] = temp;
}
}
return arr;
}
完整测试代码
package org.cloud.algorithm.sort;
import java.util.Arrays;
public class SimpleDemo {
//冒泡排序
public static void bubbleSort(int arr[]) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// swap arr[j+1] and arr[j]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
//选择排序
public static void selectSort(int arr[]) {
int n = arr.length;
// One by one move boundary of unsorted subarray
for (int i = 0; i < n - 1; i++) {
// Find the minimum element in unsorted array
int min_idx = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
}
// Swap the found minimum element with the first element
if (min_idx != i) {
int temp = arr[min_idx];
arr[min_idx] = arr[i];
arr[i] = temp;
}
}
}
/**
* 排序后,针对相同的值,排序后的顺序与原来的顺序一致
* Input : 4A 5 3 2 4B 1
* Output : 1 2 3 4A 4B 5, 即针对相同的值,排序后顺序与排序前一致
*
* @param arr
*/
static void selectStableSort(int[] arr) {
int n = arr.length;
// Iterate through array elements
for (int i = 0; i < n - 1; i++) {
// Loop invariant : Elements till a[i - 1] are already sorted.
// Find minimum element from arr[i] to arr[n - 1].
int min = i;
for (int j = i + 1; j < n; j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
// Move minimum element at current i. 为了保证之前的顺序
int key = arr[min];
while (min > i) {
arr[min] = arr[min - 1];
min--;
}
arr[i] = key;
}
}
public static void insertSort(int arr[]) {
int n = arr.length;
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
/* Move elements of arr[0..i-1], that are
greater than key, to one position ahead
of their current position */
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
//折半插入排序
public static int[] binaryInsertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
// arr[i]需要向前移动
if (arr[i] < arr[i - 1]) {
// 临时变量,存储当前下标的值
int temp = arr[i];
int j = i - 1;
// 从下标为0开始
int low = 0;
// 前一个值结束
int high = i - 1;
// 折半查找,有效的减少后续比较次数,循环结束后,high的值 +1 就是temp要插入的位置
while (low <= high) {
int mid = (low + high) / 2;
if (temp < arr[mid]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
// 从j(i-1)开始,往后移动,直到high +1,也就是要插入的位置
// 比temp(arr[i])大的值向后移动一位
for (; j >= high + 1; j--) {
arr[j + 1] = arr[j];
}
arr[high + 1] = temp;
}
}
return arr;
}
/* Prints the array */
public static void printArray(String msg, int arr[]) {
int n = arr.length;
System.out.print(msg + ":");
for (int i = 0; i < n; ++i) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// Driver method to test above
public static void main(String args[]) {
int arr[] = {
64, 34, 12, 12, 25, 12, 22, 11, 90};
bubbleSort(arr);
printArray("bubbleSort", arr);
selectSort(arr);
printArray("selectSort", arr);
selectStableSort(arr);
printArray("selectStableSort", arr);
insertSort(arr);
printArray("insertSort", arr);
binaryInsertSort(arr);
printArray("binaryInsertSort", arr);
}
}