浅谈堆(Heap)
Heap
- 简介
-
- 二叉堆
- 配对堆
- 左偏树
- 随机堆
- 斜堆
- 占位
- 运用
-
- 堆排序
- 对顶堆
简介
堆是一颗特殊的树,树中每个节点的值都 大 / 小 大 / 小 大/小 于其子节点。
每个节点值大于其子节点的,被称为大根堆。
每个节点值小于其子节点的,被称为小根堆。
我们习惯性将 二 叉 堆 二叉堆 二叉堆 简称为 堆 堆 堆。
也因此,在许多地方对堆都有这样的描述:
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。
(摘自 百度百科)
当然读者也可以从一般意义的堆开始,比如配对堆,它只对一般意义上的堆进行了合并操作的“优化”。
堆通常支持一系列操作:
| Function | Description |
|---|---|
| build | 创建一个堆 |
| find | 查找堆中最 大 \ 小 元素 |
| insert | 向堆中插入一个元素 |
| delete | 删除堆中最 大 \ 小 元素 |
在部分操作时,我们还需要一些额外的操作来维护堆的性质。
这部分放在下面讨论。
二叉堆
二叉堆作为最常用的堆结构,在不做限定时将堆与二叉堆划等号,倒也没什么不妥。
二叉堆除了堆的基本性质以外,还有
二叉堆通常是或近似一颗完全二叉树。
为了让不熟悉二叉堆的读者过多的纠结,
对此需要引用如下解释:
A binary heap must conform to both the heap property (as you discussed) and the shape property (which mandates that it is a complete binary tree). Without the shape property, one would lose the runtime advantage that the data structure provides (i.e. the completeness ensures that there is a well defined way to determine the new root when an element is removed, etc.)
重点在后半段,翻译一下就是:
失去了完全性,就会失去数据结构所提供的运行时优势。(也就是说,完全性确保了在删除元素时有一个很好的方法来确定新的根,等等)
(摘自 Stack Overflow)
此外掌握二叉堆还需要知道完全二叉树层序序列表示方法,
因为堆通常是一个可以被看做一棵完全二叉树的数组对象,
如图:
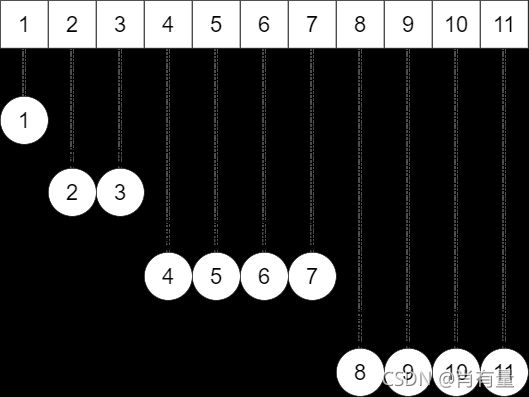
用序列表示完全二叉树时,以 1 1 1 为根节点,那么第 i i i 个节点两个儿子的下标为 i × 2 i × 2 i×2 和 i × 2 + 1 i × 2 + 1 i×2+1,反之第 i i i 个节点父节点为 ⌊ i ÷ 2 ⌋ \lfloor i ÷ 2\rfloor ⌊i÷2⌋。
现在我们声明一个保存层序序列的数组,并声明一个整形变量保存堆元素的大小,以辅助后面堆的维护操作。
import java.util.Arrays;
public class Heap {
private int size;
private int[] heap;
private Comparator comparator;
public Heap() {
this(0, (a, b) -> a == b ? 0 : a > b ? 1 : -1); }
public Heap(int size, Comparator comparator) {
this.comparator = comparator;
this.heap = new int[size];
this.clear();
}
private void swap(int i1, int i2) {
int temp = heap[i1];
heap[i1] = heap[i2];
heap[i2] = temp;
}
public void clear() {
this.size = 0; }
private void ensureCapacity(int size) {
if (size >= heap.length)
heap = Arrays.copyOf(heap, size * 3 / 2 + 1);
}
//使用比较器来增加代码重用性
public interface Comparator {
int compare(int a, int b); }
private int compare(int i1, int i2) {
return comparator.compare(heap[i1], heap[i2]); }
}
现在来考虑插入操作,如果从树也就是heap[1]开始比较,直到合适的插入位置,这样做势必会破坏层序序列的准确性。
于是我们选择插入元素置入堆底heap[size + 1],然后用上浮swim(size +1)的方式来维护堆性质。
这里以图示堆插入3为例:
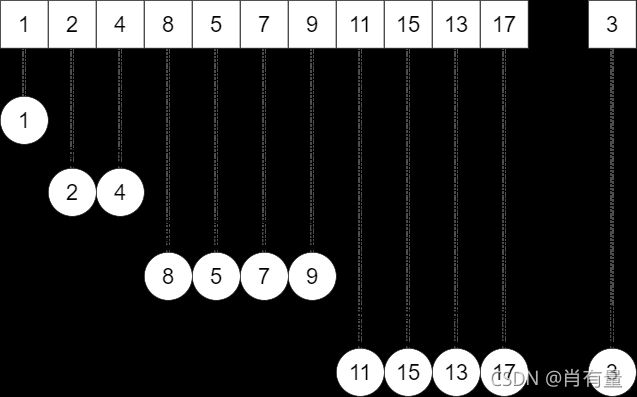
我们将插入的节点与父节点比较,如若插入节点小于其父节点,将其交换,直至插入节点为根或插入节点大于父节点,对于大根堆则恰反。
public void insert(int val) {
ensureCapacity(++size);
heap[size] = val;
swim(size);
}
private void swim(int k) {
while (k > 1 && compare(heap[k], heap[k >> 1]) < 0)
swap(k, k >>= 1);
}
用其他编程语言实现应先测试swap(k, k >>= 1)是否与当前实现意义相同。
对于查找操作,只需反复根节点下标的值即可。
public int find() {
return heap[1]; }
对于删除操作,我们先将根节点与末尾节点交换,然后直接将末尾元素移除,
虽然此举保证了层序序列的准确性,但堆的性质遭到了破坏。
对此我们可以思考上浮swim的逆过程下沉sink。
swap(1, size) and delete(size):
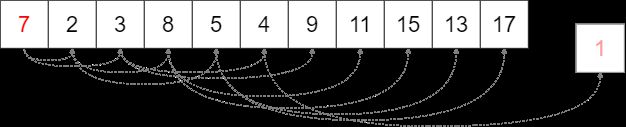
将现在的根与子节点中节点值最小的子节点交换,迭代此过程,直至子节点都大于自己。
public void delete() {
swap(1, size--);
sink(1);
}
private void sink(int k) {
while (k << 1 <= size) {
int t = k << 1;
if (t + 1 <= size && compare(t + 1, t) < 0) t++;
if (compare(k, t) < 0) return;
swap(t, k);
k = t;
}
}
二叉堆的基本操作到此就完成了。
对于插入和删除操作,交换次数不会超过堆的高度,也就是 log n \log n logn,这两项操作也能保证在 O ( log n ) O(\log n) O(logn)的复杂度下完成。
配对堆
配对堆是一种支持插入,查询 / 修改最值,合并的数据结构,是可并堆的一种。
配对堆通常是一颗带权多叉树,节点权值满足堆性质,如图:
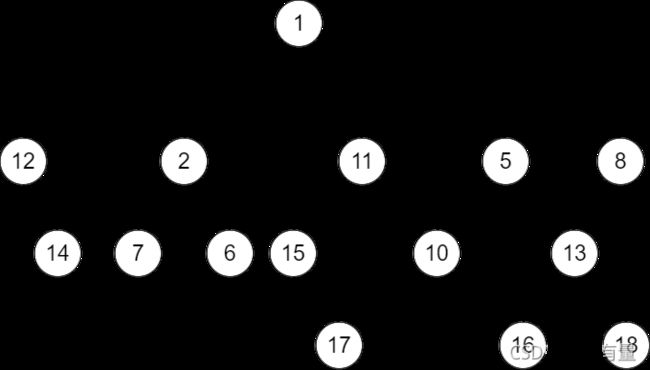
先不去计较 “配对” 的由来,我们先按堆性质建起多叉树,
这里为了提升 “配对” 性能,采用了左儿子右兄弟表示法。
public class Heap {
private Comparator comparator = (arg1, arg2) -> (arg1 < arg2);
private boolean less(int arg1, int arg2) {
return comparator.less(arg1, arg2); }
//使用比较器来增加代码重用性
public interface Comparator {
boolean less(int a, int b); }
public class Node {
int val;
Node child, sibling;
Node(int val) {
this.val = val; }
}
}
首先是建堆,直接声明一个根的引用即可。
private Node root = null;
由于配对堆的可并性,对于插入我们只需要把现有的堆与之合并即可。
public void insert(int val) {
this.root = merge(root, new Node(val)); }
合并的操作及其简单,对于小根堆,我们只需将根节权值点较大的一方设成另一方的节点即可,对于大根堆则恰反。
Node merge(Node node1, Node node2) {
if (node1 == null) return node2;
if (node2 == null) return node1;
if (less(node2.val, node1.val))
return merge(node2, node1);
node2.sibling = node1.child;
node1.child = node2;
return node1;
}
查询直接返回根节点的值即可。
public int find() {
return root.val; }
前面的几个操作完全没有对数据结构进行维护,虽然均摊下来插入能在 O ( 1 ) O(1) O(1) 的时间复杂度内完成,但当我们设计删除方案,也就是拿掉根节点时,整个堆变成了森林!诚然,我们可以对森林一一合并,但在最差情况下,时间复杂度会退至 O ( n ) O(n) O(n)。
到这里或许就能明白,二叉堆和完全性为什么密不可分,为什么它能是使用范围最广的堆结构了,不过二叉堆并非可并堆,这点留给读者自己思考。
继续来处理这片森林,在合并森林时,一个比较优秀的策略是从左至右两两配对,再从右至左朴素的拼接起来(见下图),均摊下来这样的删除操作,复杂度在 O ( log n ) O(\log n) O(logn)。
森林:
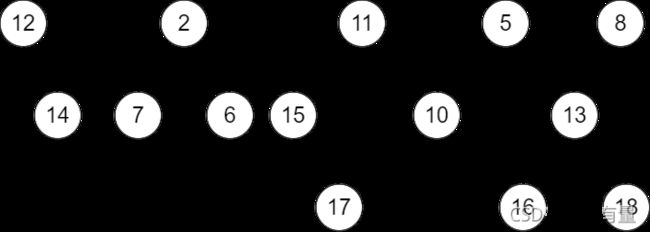
配对:
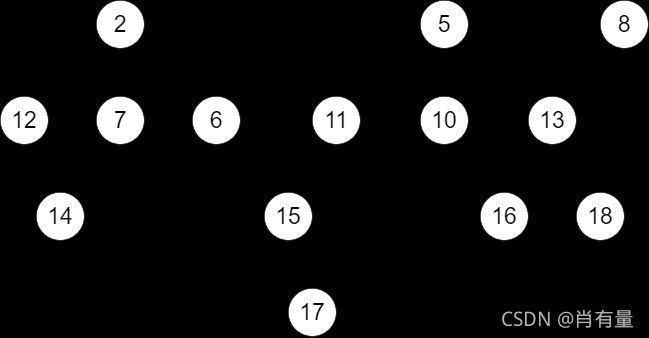
合并:

可以见到的是,配对堆可视化后形状是奇奇怪怪的。
画了就懒的删了,下面再给出一个比较直观的例子。
void delete() {
this.root = merge(root.child); }
Node merge(Node node) {
if (node == null || node.sibling == null) return node;
Node pair = node.sibling;
Node next = pair.sibling;
node.sibling = pair.sibling = null;
return merge(merge(node, pair), merge(next));
}
原堆:
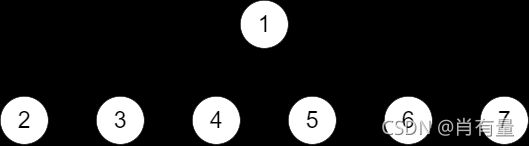
森林:

配对:

合并:

可预见的删除操作,耗时与根节点子节点数量挂钩,最差情况下是根节点儿子的兄弟退化成链表,也就是复杂度升至 O ( n ) O(n) O(n),但从上例来看,配对合并后,根节点的子节点明显减少,均摊的复杂度也是从此而来。
左偏树
左偏树是可并堆的一种,同时左偏树也是一颗二叉树。
除了权值、左子树引用、右子树引用以外,它的每个节点还包含了dist信息。
public class LeftistHeap {
private Comparator comparator;
LeftistHeap() {
this((a, b) -> a == b ? 0 : a > b ? 1 : -1); }
LeftistHeap(Comparator comp) {
this.comparator = comp; }
public interface Comparator {
int compare(int a, int b); }
private int compare(int arg1, int arg2) {
return comparator.compare(arg1, arg2); }
private class Node {
int val, dist;
Node left, right;
Node(int val) {
this(val, -1); }
Node(int val, int dist) {
this.val = val;
this.dist = dist;
}
}
}
但且仅当一个节点左子树或右子树为空时,我们称之为外节点。
dist的定义为,外节点的dist为0,空节点的dist为-1。除此以外,节点的dist为子树最近外节点dist + 1。
左偏树中,一个节点的左儿子的dist总是不小于右儿子的dist,同时它还需要具备堆性质。
你也可以调转这个定义写出右偏树
也因此,节点的dist总是它的右儿子的dist + 1。
对于一颗有 n n n 个节点的左偏树,它的根节点的dist总是不超过 ⌈ log ( n + 1 ) ⌉ \lceil \log (n +1) \rceil ⌈log(n+1)⌉,但这并不代表左偏树的深度有保障,一个退化成链表的数再长它的dist也只是0。
接下来从代码说起吧。
首先是建堆,定义变量保存根节点引用即可。
private Node root = null;
插入还是以合并的方式实现。
public void insert(int val) {
this.root = merge(root, new Node(val)); }
对于合并操作,我们需要同时维护堆性质和左偏树性质。
对于小根堆,
维护堆性质只需将根节点较小的节点的右子树与另一节点合并,
而维护左偏树性质,我们需要在每一次合并后比较两个儿子的dist,当不满足左偏树性质时,将其交换,然后更新自身的dist。
由于左偏树的性质,合并时每向下一层,dist相应就会减少1,同时大小为 n n n 的左偏树的根节点的dist总是不超过 ⌈ log ( n + 1 ) ⌉ \lceil \log (n +1) \rceil ⌈log(n+1)⌉,这样意味着在合并大小分别为 n n n、 m m m 的左偏树,最坏情况下复杂度也不过是 O ( log n + log m ) O(\log n + \log m) O(logn+logm)。
private Node merge(Node node1, Node node2) {
if (node1 == null) return node2;
if (node2 == null) return node1;
if (compare(node1.val, node2.val) > 0)
return merge(node2, node1);
node1.right = merge(node1.right, node2);
if (node1.left == null) {
node1.left = node1.right;
node1.right = null;
} else
if (compare(node1.dist, node2.dist) < 0) {
Node temp = node1.left;
node1.left = node1.right;
node1.right = temp;
}
node1.dist = node1.right == null ? 0 : node1.right.dist + 1;
return node1;
}
查询不谈。
public int find() {
return root.val; }
由于左偏树是一颗二叉树,在拿掉根节点后只会出现两片森林,直接将其合并就行,该操作同样能在对数复杂度下完成。
public void delete() {
this.root = merge(root.left, root.right); }
由于需要存储额外的信息,而且合并起来常数也较大,因此在基本操作中,左偏树并没有什么优势。
但在给定集合的情况下建起一颗左偏树,可以做到线性时间内完成。
我们使用一个队列,最开始将集合中所有元素建立对应节点入列,
从列队中不断取出两个节点合并,然后加入队尾,直至队列中只剩一个元素,这个元素就是左偏的根,
整个过程可以在 O ( n ) O(n) O(n) 的复杂度下完成。
LeftistHeap(int[] A) {
this();
Queue<Node> queue = new ArrayDeque();
for (int val : A)
queue.offer(new Node(val));
while (queue.size() > 1)
queue.offer(merge(queue.poll(), queue.poll()));
this.root = queue.size() == 0 ? null : queue.poll();
}
完事.
随机堆
一定程度上属于一种摆烂的写法。
详细的分析指路 randomized_heap.md。
这里只做简单的实现和对比。
import java.util.ArrayDeque;
import java.util.Queue;
public class RandomizedHeap {
private Node root = null;
private Comparator comparator;
RandomizedHeap() {
this((a, b) -> a == b ? 0 : a > b ? 1 : -1); }
RandomizedHeap(int[] A) {
this();
Queue<Node> queue = new ArrayDeque();
for (int val : A)
queue.offer(new Node(val));
while (queue.size() > 1)
queue.offer(merge(queue.poll(), queue.poll()));
this.root = queue.size() == 0 ? null : queue.poll();
}
RandomizedHeap(Comparator comp) {
this.comparator = comp; }
public void insert(int val) {
this.root = merge(root, new Node(val)); }
public int find() {
return root.val; }
public void delete() {
this.root = merge(root.left, root.right); }
private Node merge(Node node1, Node node2) {
if (node1 == null) return node2;
if (node2 == null) return node1;
if (compare(node1.val, node2.val) > 0)
return merge(node2, node1);
if (Math.random() <= 0.5)
node1.left = merge(node1.left, node2);
else
node1.right = merge(node1.right, node2);
return node1;
}
public interface Comparator {
int compare(int a, int b); }
private int compare(int arg1, int arg2) {
return comparator.compare(arg1, arg2); }
private class Node {
int val;
Node left, right;
Node(int val) {
this.val = val; }
}
}
提交到 洛谷 P3378. 【模板】堆。
左偏树:

随机堆:

事实上随机化的算法,多数情况下表现强劲,而且极难捏出接近上界的数据。
个人能力有限,没货讨论了。
斜堆
斜堆是左偏树的一种特殊形式,但斜堆不具备左偏性质,并且在斜堆中没有dist概念。
同样的,斜堆是一颗堆有序二叉树。
在左偏树中,每一次合并都是沿着右路径进行,合并后最右路径长度必然增加,这样会影响下一次合并的效率。
所以合并后视情况交换左右子树,使得右路径极大缩小。
由于斜堆不记录dist信息,因此斜堆在每次合并后直接交换左右节点,以减少最右路径长度。
也因此斜堆和左偏树的区别,只是在于少记录一个信息和合并策略上,从这个角度看,随机堆也是左偏树的一个变种。
// 班会,晚上回来写。
占位
运用
堆排序
现在我们知道了二叉堆在插入和删除最值时都有着优秀的时间复杂程度,这意味着,基于堆进行的排序时间复杂度在最坏的情况下也只是 O ( n log n ) O(n \log n) O(nlogn),并且它可以做到不需要额外的辅助空间,原地进行排序。
一种比较朴素的想法是我们对原数组A进行遍历,遍历到i时执行swim(i)操作,当堆建立完毕后,从后往前和首元素进行交换,然后执行sink(i - 1)操作维护堆性质。
但我们站在了巨人的肩膀上,
我们把二叉堆中,每个叶子节点当做一个大小为1的堆,然后自底向上枚举每个非叶节点,将枚举到的节点视为一次堆的合并,执行sink(i)操作。
从上自下的建堆,在最坏情况下需要 O ( 1 × 2 1 + 2 × 2 2 + . . . + ⌊ log n ⌋ × 2 ⌊ log n ⌋ ) O(1 × 2^1 + 2 × 2^2 + ... + \lfloor\log n\rfloor × 2^{\lfloor\log n\rfloor}) O(1×21+2×22+...+⌊logn⌋×2⌊logn⌋),也就是接近 n log n 2 \cfrac{n \log n}{2} 2nlogn 次交换,而自底向上建堆则至多有 O ( 1 × 2 ⌊ log n ⌋ + 2 × 2 ⌊ log n − 1 ⌋ + . . . + ⌊ log n ⌋ × 1 ) O(1 × 2^{\lfloor\log n\rfloor} + 2 × 2^{\lfloor\log n - 1\rfloor} + ... +\lfloor\log n\rfloor × 1) O(1×2⌊logn⌋+2×2⌊logn−1⌋+...+⌊logn⌋×1),接近 2 n 2n 2n 次交换,高判立下了家人们。
public class Main {
public static void main(String[] args) {
new Main().run(); }
public void run() {
sort(A, 1, n);
}
public void sort(int[] A, int start, int end) {
int offset = start - 1;
for (int i = end - start + 1 >> 1; i >= 1; i--)
sink(A, offset, i, end - offset);
while (end > start) {
swap(A, start, end--);
sink(A, offset, 1, end - offset);
}
}
private void sink(int[] A, int offset, int k, int n) {
while (k << 1 <= n) {
int temp = k << 1;
if (temp < n && A[offset + temp + 1] > A[offset + temp]) temp++;
if (A[offset + temp] <= A[offset + k]) return;
swap(A, offset, k, temp);
k = temp;
}
}
private void swap(int[] A, int offset, int i, int j) {
int temp = A[offset + i];
A[offset + i] = A[offset + j];
A[offset + j] = temp;
}
private void swap(int[] A, int i, int j) {
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}
需要注意的是,我们想要运用层次序列的性质的话,通常必须得满足根节点在序号1的位置,所以这里定义了偏移量offset,具体的细节就不展开讲了。
对顶堆
对顶堆则是一种堆的使用方法,在处理动态 top k 这类问题时较为有效。
这里以解决 POJ 3784. Running Median 举例。
我们在求解 top k 问题时,可以维护同时两个堆A、B,如果保证了A中的元素都大于B中的元素,且A为小根堆同时大小为k,
显然,此时 top k 为A的堆顶元素。
而为了维护这个性质,当B的大小大于n - k时,我们需要将B中最大的元素拿出,放入A中,因此B为大根堆。
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) {
new Main().run(); }
void run() {
InputReader in = new InputReader(System.in);
PrintWriter out = new PrintWriter(System.out);
Heap heap1 = new Heap((a, b) -> a < b);
Heap heap2 = new Heap((a, b) -> a > b);
int p = in.readInt();
while (p-- > 0) {
heap1.clear();
heap2.clear();
int median = 0x80000000;
int k = in.readInt();
int m = in.readInt();
boolean odd = false;
boolean flag = m % 20 != 0;
out.printf("%d %d\n", k, m + 1 >> 1);
for (int i = 1; i <= m; i++) {
int val = in.readInt();
if (val >= median)
heap1.insert(val);
else
heap2.insert(val);
if (heap2.size() > i >> 1)
heap1.insert(heap2.delete());
if (heap1.size() > i + 1 >> 1)
heap2.insert(heap1.delete());
median = heap1.find();
if (odd = !odd)out.print(median);
out.print(i % 20 == 0 ? '\n' : ' ');
}
if (flag) out.print('\n');
}
out.flush();
}
public static class Heap {
int size;
int[] heap;
Comparator comp;
public Heap() {
this((a, b) -> a < b); }
public Heap(Comparator comp) {
this.heap = new int[8];
this.comp = comp;
this.clear();
}
public void insert(int val) {
ensureCapacity(++size);
heap[size] = val;
swim(size);
}
public int find() {
return heap[1]; }
public int delete() {
int temp = heap[1];
heap[1] = heap[size--];
sink(1);
return temp;
}
public int size() {
return size; }
public boolean isEmpty() {
return size == 0; }
private void swim(int k) {
while (k > 1 && less(k, k >> 1))
swap(k, k >>= 1);
}
private void sink(int k) {
while (k << 1 <= size) {
int temp = k << 1;
if (temp + 1 <= size && less(temp + 1, temp)) temp++;
if (less(k, temp)) return;
swap(k, temp);
k = temp;
}
}
private boolean less(int i1, int i2) {
return comp.less(heap[i1], heap[i2]); }
private void swap(int i1, int i2) {
int temp = heap[i1];
heap[i1] = heap[i2];
heap[i2] = temp;
}
private void ensureCapacity(int size) {
if (size >= heap.length)
heap = Arrays.copyOf(heap, size * 3 / 2 + 1);
}
public void clear() {
this.size = 0; }
interface Comparator {
boolean less(int a, int b); }
}
public class InputReader {
BufferedReader reader;
StringTokenizer token;
InputReader(InputStream in) {
this.reader = new BufferedReader(new InputStreamReader(in));
}
String read() {
while (token == null || !token.hasMoreTokens()) {
try {
token = new StringTokenizer(reader.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return token.nextToken();
}
int readInt() {
return Integer.parseInt(read()); }
}
}
这里用了 lambda表达式,需要 java8 以上才可编译运行。
开个坑,找时间慢慢写。