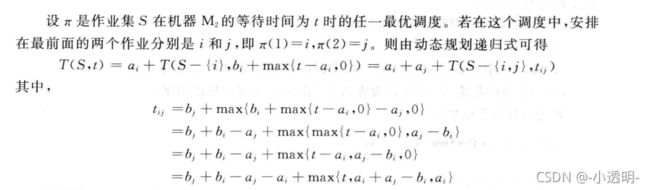动态规划之流水作业调度问题

描述：n个作业{1,2,3....,n}要在两台机器M1,M2组成的流水线上加工完成。每个作业的加工顺序都是先在M1上加工，然后在M2上作业加工。M1，M2加工作也i所需的时间分别为ai和bi(1<=i<=n)。流水作业调度问题要求确定这n个作业的最优加工顺序，使得从第一个作业在机器M1上开始加工，到最后一个作业在机器M2上加工完成所需的时间最少。

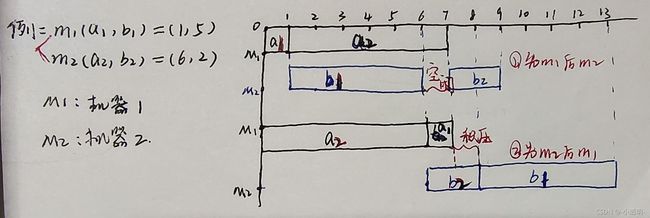
一个最优调度应该使机器M1没有空闲时间，且机器M2的空闲时间最少，一般情况下，机器M2上会出现 机器空闲 和 作业积压 两种情况。用m(a,b)表示m任务需要在M1机器加工a分钟，在M2上需要b分钟。更直观的看，上述情况可由下图体现出来。

 如图所示，如果先加工m1后加工m2，需要时间9t；反过来，需要时间13t，因此第一种情况更优

一定要该清楚每个变量代表着什么意思，要不一会儿就懵了！

设全部作业集合N={1,2,3，...，m}，SN是N 的作业子集，一般情况下，机器M1开始加工S中的作业时，机器M2还在加工其他作业，需要等时间t后才可利用。将这种情况下完成S中作业所需最短时间记为T(S,t)。该问题的最优值为T(N,0)。 

下面开始动态规划的四个步骤进行分析：

1. 最优子结构

设π是所给n个流水作业的一个最优调度，所需的加工时间为aπ(1)+T`。其中，T`是在机器M2的等待时间为bπ(1)时，安排作业π(2),...,π(n)所需的时间。记S=N-{π(1)}，则有T`=T(S,bπ(1))。可说明其具有最优子结构性质。

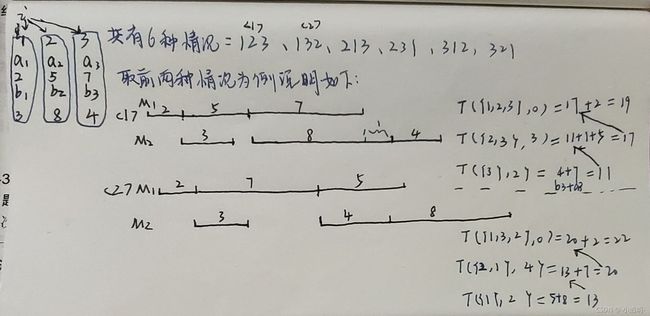
选题目中前三个为例，更直观的说明一下（反正我看这些表达式是懵的，还是举个例子比较清晰）

2. 递归计算最优值

由最优子结构性质可得T(N,0)=min{ai+T(N-{i},bi)} <1<=i<=n>推广到T(S,t)，有：

T(S,t)=min{ai + T（S-{i}，bi + max{t-ai}，0) }(i∈S）

max{t-ai} 是由于机器M2上，作业i必须在max{t-ai}时间后才能开工。因此在机器M1上完成作业i之后，在机器上还需bi+max{t-ai}-ai=bi+max{t-ai, 0}时间，才能完成作业 i 的加工。（这个数学公式又是为什么呢？具体过程如下图所示。）

 虽然满足最优子结构性质，也在一定程度满足子问题重叠性质。N的每个非空子集S都计算一次，共次，达到了指数级。因此引入 Johnson法则 解决这个问题。

3. 流水调度的Johnson法则

这个推导过程看不懂没关系，只要知道：

如果作业i和j满足min{bi,ai}>=min{bj,ai},则称作业i，j满足Johnson不等式；如果i和j不满足不等式，则交换i，j的加工顺序后，既满足 Johnson不等式

这一大串分析只为了得出一个结论：流水作业调度问题一定存在满足Johnson法则的最优调度。

4. 算法描述

上面的推导实在看着头疼，记住结论就好：

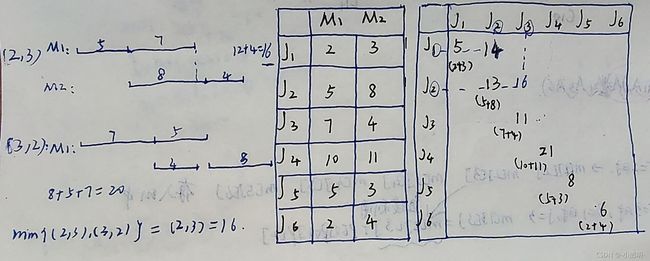
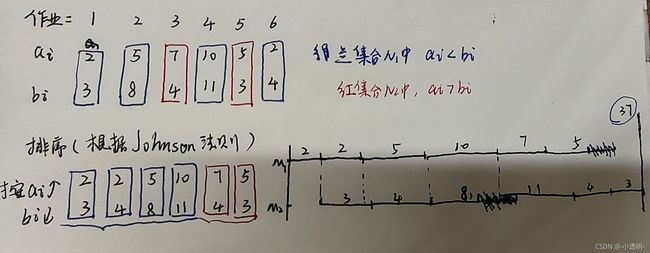
将对应的ai和bi放在一起；将ai>bi的放在一起，ai

 来一个具体问题康康吧！ 

动态规划的思路，类似矩阵连乘

 Johnson算法：

1)先执行t[i,1] 即t[i,1]越小，越靠前执行;
2)执行t[i,1]>=t[i,2]时，要保证最后一个作业在M2上执行时间最短，所以按照减序排列

 具体代码如下：

#include 
#include 
#include 
using namespace std;
const int N=50;

class Job { //作业类
public:
    int index, time;//作业编号和时间
    bool M;//true代表机器M1, false代表机器M2
};

bool cmp(Job a,Job b){ //升序排序
    return a.time=bi的分到N2组
            Min[i].M=false;
            Min[i].time=b[i];
        }
        Min[i].index=i;
    }
    sort(Min, Min+n, cmp);//增序排列
    j=0,k=n-1;
    for(i=0;i>n;
    for(i=0;i>a[i];
    for(i=0;i>b[i];
    infile.close();

    outfile.open("output1.txt");
    outfile<<"the best order is:"<

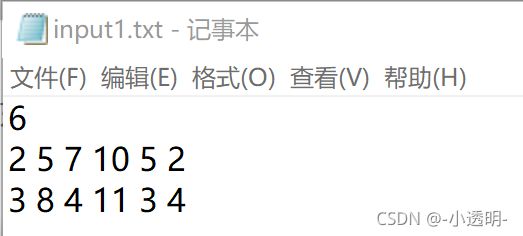
读取的输入文件如下图所示：

运行后输出文件如下图所示： 

时间复杂度分析：计算时间花在对作业的排序上，最坏情况下，为O（logn），空间0（n）