数据结构 图论07 Floyd算法详解 通俗易懂
Floyd 算法详解
Floyd 算法是 所有点到所有点 的最短路径的算法,阅读前请想了解图的数据结构「邻接矩阵」
邻接矩阵
Floyd 算法是一个基于「贪心」、「动态规划」求一个图中 所有点到所有点 最短路径的算法,时间复杂度 O(n3)
1. 要点
以每个点为「中转站」,刷新所有「入度」和「出度」的距离。
Dijkstra 算法:每次从「未求出最短路径」的点中 取出 最短路径的点,并通过这个点为「中转站」刷新剩下「未求出最短路径」的距离。
Dijkstra 的算法在图中的效果像是:以起点为中心像是一个涟漪一样在水面上铺开。
Floyd 算法在图中的效果像是:一个一个多点的小涟漪,最后小涟漪铺满整个水面。
2.图解案例分析
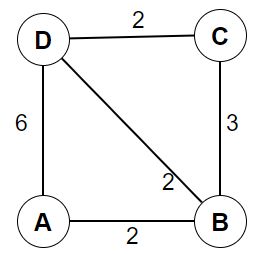
案例:求所有点到所有点的最短距离
邻接矩阵图
int[][] graph = new int[][]{
{
0 , 2, ∞, 6}
{
2 , 0, 3, 2}
{
∞ , 3, 0, 2}
{
6 , 2, 2, 0}};
(重点)算法要点
distance[][]:用来储存每个点到其他点的最短距离path[][]:用来储存每个点到其他点最短距离的路径
要点:以每个点为「中转站」,刷新所有「入度」和「出度」的距离。
所以我们要:遍历每一个顶点 --> 遍历点的每一个入度 --> 遍历每一个点的出度,以这个点为「中转站」距离更短就刷新距离(比如 B 点为中转站 AB + BD < AD 就刷新 A 到 D 的距离)
2.1. 初始化:
初始化距离 distance 为图结构 graph,初始化路径 path 为初始图结构的路径如下
====distance====
0 2 -1 6
2 0 3 2
-1 3 0 2
6 2 2 0
====path====
0 1 2 3
0 1 2 3
0 1 2 3
0 1 2 3
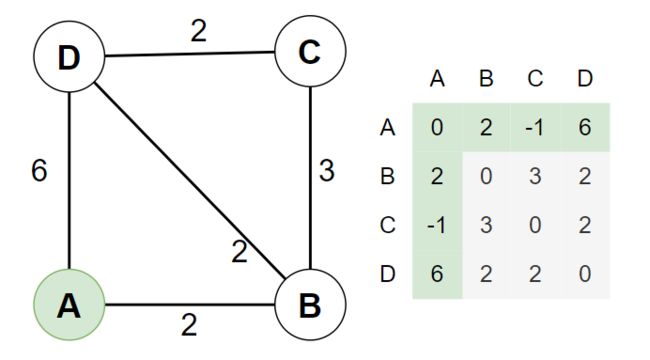
2.2. 以 A 为「中转站」,刷新所有「入度」和「出度」的距离
A 的入度有 B 、D 2点,A 的出度也是 B、D 2点
BA + AD > BD
DA + AB > DB
所以没有更小的距离,不能「刷新距离」,distance[][] 和 path[][] 不刷新
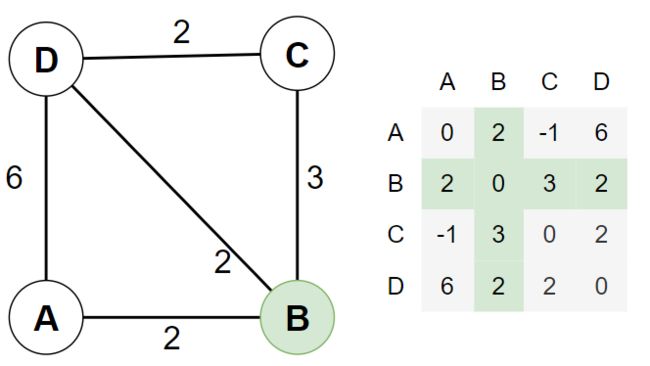
2.3. (重点)以 B 为「中转站」,刷新所有的「入度」和「出度」的距离
B 的入度有 A、C、D;B 的出度有 A、C、D。(所以一共有 6 种组合)
AB + BC < AC ( 2 + 3 < 无穷大,这里的 -1 代表无穷大)
- 刷新距离:
- 刷新距离:将 AB + BC 的距离 5 赋值给 AC 距离 -1,即
distance[0][2] = distance[0][1] +distance[1][2] - 刷新最短路径:AC 的最短距离不再是直线 AC 的最短距离,引入「中转站」B 点,即
path[0][2] = 1
- 刷新距离:将 AB + BC 的距离 5 赋值给 AC 距离 -1,即
AB + BD < AD ( 2 + 2 < 6)
- 刷新距离:
- 刷新距离:将 AB + BD = 4 的值赋值给 AD,即
distance[0][3] = distance[0][1] +distance[1][3] - 刷新最短路径:AD的最短距离不再是直线 AD 的最短距离,引入「中转站」B 点,即
path[0][3] = 1
- 刷新距离:将 AB + BD = 4 的值赋值给 AD,即
CB + BA < CA( 2 + 3 < 无穷大 同理第一个 AB + BC < AC ,刷新距离)
CB + BD > CD(3 + 2 > 2,不用刷新距离)
DB + BA < DA (2 + 2 < 6,同理第二个 AB + BD < AD, 刷新距离)
DB + BC < DC(2 + 3 < 2 ,不用刷新距离)
刷新后的 distance[][] 和 path[][] 入下所示
====distance====
0 2 5 4
2 0 3 2
5 3 0 2
4 2 2 0
====path====
0 1 1 1
0 1 2 3
1 1 2 3
1 1 2 3
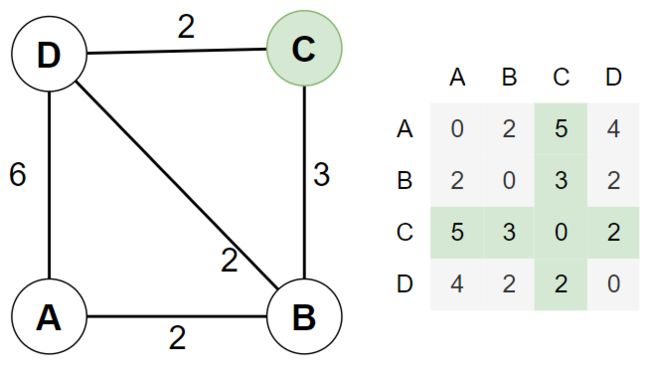
2.4. 以 C 点为「中转站」,刷新所有「出度」和「入度」的距离
类似 3 步骤,这里不赘述
2.5. 以 D 点为「中转站」,刷新所有「出度」和「入度」的距离
类似 3 步骤,这里不赘述,结束算法
3. 代码
这里使用 -1 表无穷大,下面是 Java 代码和测试案例
package floyd;
/**
* @author Jarvan
* @version 1.0
* @create 2020/12/25 11:01
*/
public class Floyd {
/**
* 距离矩阵
*/
public static int[][] distance;
/**
* 路径矩阵
*/
public static int[][] path;
public static void floyd(int[][] graph) {
//初始化距离矩阵 distance
distance = graph;
//初始化路径
path = new int[graph.length][graph.length];
for (int i = 0; i < graph.length; i++) {
for (int j = 0; j < graph[i].length; j++) {
path[i][j] = j;
}
}
//开始 Floyd 算法
//每个点为中转
for (int i = 0; i < graph.length; i++) {
//所有入度
for (int j = 0; j < graph.length; j++) {
//所有出度
for (int k = 0; k < graph[j].length; k++) {
//以每个点为「中转」,刷新所有出度和入度之间的距离
//例如 AB + BC < AC 就刷新距离
if (graph[j][i] != -1 && graph[i][k] != -1) {
int newDistance = graph[j][i] + graph[i][k];
if (newDistance < graph[j][k] || graph[j][k] == -1) {
//刷新距离
graph[j][k] = newDistance;
//刷新路径
path[j][k] = i;
}
}
}
}
}
}
/**
* 测试
*/
public static void main(String[] args) {
char[] vertices = new char[]{
'A', 'B', 'C', 'D'};
int[][] graph = new int[][]{
{
0, 2, -1, 6}
, {
2, 0, 3, 2}
, {
-1, 3, 0, 2}
, {
6, 2, 2, 0}};
floyd(graph);
System.out.println("====distance====");
for (int[] ints : distance) {
for (int anInt : ints) {
System.out.print(anInt + " ");
}
System.out.println();
}
System.out.println("====path====");
for (int[] ints : path) {
for (int anInt : ints) {
System.out.print(anInt + " ");
}
System.out.println();
}
}
}
测试结果
====distance====
0 2 5 4
2 0 3 2
5 3 0 2
4 2 2 0
====path====
0 1 1 1
0 1 2 3
1 1 2 3
1 1 2 3