手撕神经网络框架(numpy)
神经网络基本步骤
- loaddata
- initialize
- forward
- backward
- update
任何神经网络肯定都有这些基本操作过程,每一小步中又会有各种不同的策略。
我是跟着吴恩达大佬做的一些实践,对神经网络的理解特别有用
loaddata
这一步包括归一化、小批量读取等等操作。这里只做一些最简单的处理。
def load_dataset():
train_dataset = h5py.File('D:/PyWorkspace/DeepLearning/datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('D:/PyWorkspace/DeepLearning/datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
train_set_x = train_set_x_flatten / 255.
test_set_x = test_set_x_flatten / 255.
return train_set_x, train_set_y_orig, test_set_x, test_set_y_orig, classes
initialize
初始化主要就是初始化每一层之间的那些权重,即 w 和 b ,TensorFlow等框架的高级API会根据神经元的个数推算每层之间 w 和 b 的形状。
初始化有不同的策略,比如,随机初始化、何凯明提出的一种初始化等等。这里一次性把所有参数都初始化。
# GRADED FUNCTION: initialize_parameters_he
def initialize_parameters_he(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims) - 1 # integer representing the number of layers
for l in range(1, L + 1):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2.0 / layers_dims[l - 1])
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
### END CODE HERE ###
return parameters
forward
前向传播比较简单,就是:
W * X + b
矩阵相乘的过程,只是激活单元非线性函数再做一个处理。
最终到输出层,输出值与真实标签算一个损失。
算损失又有不同的策略,常见的交叉熵损失,平方损失等等。
注意:绝对值损失不怎么用的原因就是因为不好求导,而平方便于求导
def compute_cost(AL, Y):
"""
Implement the cost function defined by equation (7).
Arguments:
AL -- probability vector corresponding to your label predictions,
shape (1, number of examples)
Y -- true "label" vector (for example: containing 0 if non-cat, 1
if cat), shape (1, number of examples)
Returns:
cost -- cross-entropy cost
"""
m = Y.shape[1]
# Compute loss from aL and y.
### START CODE HERE ### ( 1 lines of code)
cost = -(np.dot(Y,np.log(AL.T))+np.dot(1-Y,np.log(1-AL).T))/m
### END CODE HERE ###
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17)
assert(cost.shape == ())
return cost
backward
反向传播应该是神经网络里最难的部分,各种神经网络框架也都屏蔽了反向传播的过程,自动微分机制。
主要用到的数学知识是链式法则,将误差从最后输出层逐渐传播到输入层。
这里不做理论推导,但要知道反向传播的四大公式:
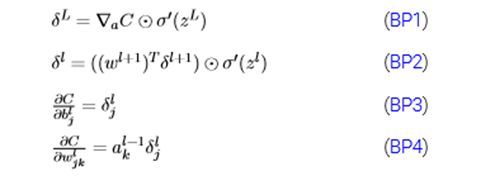
BP1算出最后一层的误差
BP2即可实现传递误差
BP3与BP4主要用来更新各层之间的权重。
def L_model_backward(AL, Y, caches):
"""
Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
Arguments:
AL -- probability vector, output of the forward propagation (L_model_forward())
Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
caches -- list of caches containing:
every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2)
the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1])
Returns:
grads -- A dictionary with the gradients
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
### START CODE HERE ### (1 line of code)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
### END CODE HERE ###
# Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
### START CODE HERE ### (approx. 2 lines)
current_cache = caches[L - 1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache,
'sigmoid')
### END CODE HERE ###
for l in reversed(range(L - 1)):
# lth layer: (RELU -> LINEAR) gradients.
# Inputs: "grads["dA" + str(l + 2)], caches".
# Outputs: "grads["dA" + str(l + 1)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)]
### START CODE HERE ### (approx. 5 lines)
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, 'relu')
grads["dA" + str(l + 1)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
### END CODE HERE ###
return grads
update
迭代过程中更新参数,逐渐优化模型。优化的策略又有多种,梯度下降、随机梯度下降、小批量梯度下降等等。
它们之间的区别主要是用于正向传播的数据量。
其中,小批量的小批量取一,则可理解为随机梯度下降。
大名鼎鼎的优化器有moment、Adam等等,具体知识自行学习。
# GRADED FUNCTION: update_parameters
def update_parameters(parameters, grads, learning_rate):
"""
Update parameters using gradient descent
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients, output of
L_model_backward , →
Returns:
parameters -- python dictionary containing your updated parameters
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural network
# Update rule for each parameter. Use a for loop.
### START CODE HERE ### ( 3 lines of code)
for l in range(L):
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l + 1)]
### END CODE HERE ###
return parameters
是不是感觉也没那么难。这里分享一下代码,及吴恩达教程。仅供参考,自行完善。
链接:https://pan.baidu.com/s/1iGQZyL1HVQak_f7AJD_KRQ
提取码:k0hu
复制这段内容后打开百度网盘手机App,操作更方便哦