第九章：序列处理与循环网络_Dan Jurafsky《自然语言处理综述》(第三版)读书笔记

9.0 前言

语言是一种时间现象。当我们理解和产出口语时，我们是在处理一个不定长度的连续输入流。即使是处理书面文本，我们通常也是按顺序来处理，虽然我们原则上是可以同时对所有元素进行任意访问的。我们常用的一些隐喻反映了语言的时间本质：我们常说语流、新闻流、推特流，这些都表明语言是随着时间展开的序列。这些时间性质，也体现在语言处理所用的算法当中。当应用于词类标注时，维特比算法是逐词输入，并沿途收集信息。后面章节的句法分析算法也类似。
相反，情感分析以及其他分类任务使用的机器学习算法不具有这种时间特性。他们可以同时处理输入的每一部分。前馈神经网络也是这样，包括神经语言模型的构建。这种网络使用固定长度的输入向量，用权重来捕获一个输入样本的全部信息。但是这样就很难处理长度不定的序列，也无法捕获语言中时间方面的先后信息。
我们见过神经语言模型处理这些问题的方法。模型使用固定大小的窗口来接受输入信息；通过滑动窗口来处理后面的序列，并不断对后词做出预测；最终的结果是一个预测出的序列。问题是，通过一个窗口得到的结果对后续的预测没有任何影响；
使用滑窗的方法有一系列问题：第一，与马尔可夫方法具有同样的弊端，限制了提取信息的语境长度。在语境窗口之外的信息对预测结果没有影响。这是一个很严重的问题，因为某些语言任务所需要的信息，与正在处理的时间点的距离是任意的；第二，窗口的使用让网络难以学到一些系统化的结构，比如固定搭配等。比如在窗口为 3 的网络中，输入时 the ground 当前如果处在窗口第二、第三的位置上，上一个时间点它们就处在第一、第二的位置，这样就强制网络学习到两个独立的搭配，而实际上它俩是一个。？
本章的主题是循环神经网络（recurrent neural network），它是一种可以解决以上问题的网络，直接处理语言的时序方面，让我们可以处理不同长度的输入，而无需使用固定大小的窗口，为我们提供了捕获和探索语言时间特性的方法。

9.1 简单的循环神经网络

在网络的连接中存在循环的网络称为循环神经网络（RNN）。也就是，在网络中的一个单元，直接或间接地把之前的一些输出作为一个输入。虽然很强大，但是这类网络却难以解释和训练。不过，在循环网络这一大类里，有一些是受限制的结构，可以很有效地应用于口语和书面语的处理中。这一部分，我们介绍 Elman 网络（1990），或者称为 简易循环网络。这类网络自身就很有用，并且可以作为更加复杂的网络的基础。后面当我们说 RNN 的时候，指的就是此类简单又受限制的网络。
下图是简易 RNN 的结构。与常规的前馈网络一样，使用一个向量表示输入 x_t，乘以一个权重矩阵，再通过一个激活函数计算得到隐藏层的一个单元值，最后再计算相应的输出 y_t 。与基于窗口的方法不同的是，序列的处理方式是网络在每个时间点处理一个元素。与前馈网络最本质的区别是图中虚线表示的循环链路。这个链路为隐藏层的计算增加了一个输入值，这个输入值来自于前一个时间点的隐藏层激活值。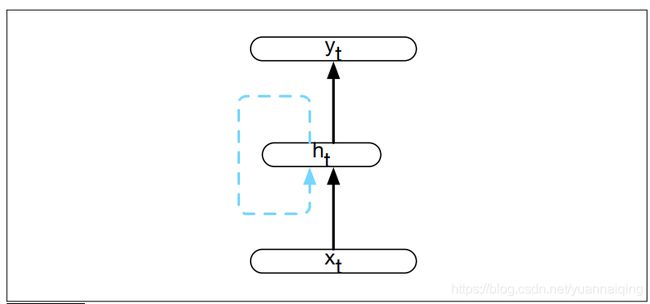
前一个时间步的隐藏层提供了记忆或者语境，把前面的处理进行了编码，然后为后续时间点的决策提供信息。很重要的一点是，这个结构对上文的长度没有要求，前一时间步的隐藏层所包含的信息，是序列从开头之后的所有信息。
添加时间维度可能让 RNN 看起来比非循环的结构更加标新立异，但是实际上并不是完全不同。加入了前一时间步隐藏层传递过来的向量作为一个输入向量，我们做的仍然是标准的向前计算。下图展示了循环的本质，以及在隐藏层中的计算过程。最大的变化是有一个新的权重矩阵 $U$，这个矩阵连接了前一时间步的隐藏层和当前时间步的隐藏层。这个权重矩阵决定了网络如何使用过往的语境信息来计算当前时间步的输出。与网络中的其他权重一样，这个连接矩阵也是通过反向给传播训练得到。

9.1.1 简易RNN中的推理

RNN 中的前向推理（将一个输入序列投射为一个输出序列）与前馈网络中的一样。使用输入 x_t 计算输出 y_t，我们需要隐藏层 h_t 的激活值，为了计算 h_t，我们需要用 x_t 乘以权重矩阵 W，用前一时间步的 h_t-1乘以权重矩阵 U，然后把两个乘积相加，得到的和再传入一个合适的激活函数 g，这样就得到了隐藏层的激活值 h_t 。之后我们就可以用常规的计算来产生输出向量了。$$h_t=g(U{h}_{t-1}+W{x}_t)$$$$y_t=f(V{h}_t)$$在常见的soft分类中，y_t 的计算涉及 softmax 计算，也就是在所有可能的输出上提供一个标准化了的概率分布。$$y_t=softmaxt(V{h}_t)$$ t 时刻的计算需要 t-1 时刻的隐藏层值，这就需要一个递进的推理算法，可以从头处理序列一直到最后。算法如下：

把循环网络展开，我们可以看到它具有的顺序特性。在下图中，每个时间步的各层和单元结构都一样，只是值不同，不过他们共享各个权重矩阵。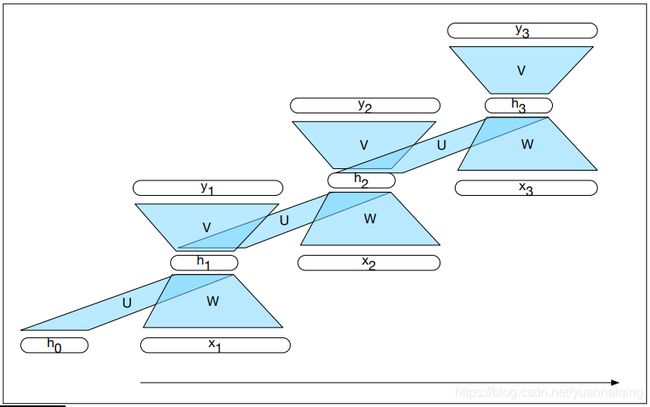

9.1.2 训练

与前馈网络一样，循环网络中我们也要用一个训练集，一个损失函数，使用反向传播的方式获得梯度然后对权重进行调整。如图 9.3 所示，我们有三个权重矩阵需要更新：W，它是输入层到隐藏层的权重；U，它是前一时间步的隐藏层到当前时间步的隐藏层的权重；V，它是隐藏层到输出层的权重。
在继续之前，我们首先复习几个第七章中的概念。假设有一个输入层为 x 、一个非线性激活函数为 g 的网络，$a^{[i]}$ 表示 $i$ 层的激活值，也就是把 $z^{[i]}$ 传入到 a 得到的结果，$z^{[i]}$ 是这一层输入的加权值。
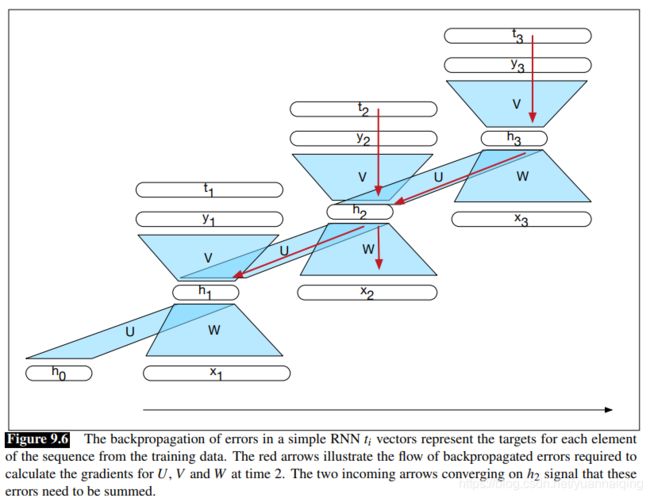
上面那图展示了两件反向传播时需要考虑的事情，它们在前馈网络中无需关注。第一，计算 t 时刻的损失函数，我们需要 t-1 时刻隐藏层；第二，t 时刻的隐藏层会同时影响 t 时刻的输出，以及 t+1 时刻的隐藏层（也就影响 t+1 时刻的输出和损失）。由此得出，为了评估 $h_t$ 产生的误差，我们需要知道它对当前输出以及后续输出产生的影响。？
我们来观察下图中时间步2的输入/输出。我们要如何计算以更新 U，V，W ？我们先来看看如何更新 V，因为这里与前馈网络是一样的，我们需要计算损失函数 L 关于权重 V 的导数。但是由于损失不是直接用权重表示的，我们使用链式法则来间接地求得。
$$\frac{\partial L}{\partial V}=\frac{\partial L}{\partial a}\frac{\partial a}{\partial z}\frac{\partial z}{\partial V}$$
公式右侧的第一项是损失函数关于网络输出 a 的导数，第二项是网络输出关于…(这段后部分感觉有误，不过影响不大。)
我们把前两项用 $\delta$ 来表示，它是一个误差项，表示输出层每个单元的变化量对损失的影响大小：$${\delta }_{out}=\frac{\partial L}{\partial a}\frac{\partial a}{\partial z}$$$${\delta }_{out}=L^{\prime }{g}^{\prime }(z)$$因此，用来更新权重矩阵 V 的最终梯度就是：$$\frac{\partial L}{\partial V}={\delta }_{out}{h}_t$$
然后，我们需要计算权重矩阵 W 和 U 的相应梯度：$\frac{\partial L}{\partial W}$ 和 $\frac{\partial L}{\partial U}$ 。这里我们遇到了第一个与前馈网络实质上的不同。t 时刻的隐藏状态影响了 t 时刻的输出以及相应的误差，也影响了 t+1 时刻的输出和也相应误差。因此，隐藏层的误差项 ${\delta }_h$ ，必定是当前输出的误差项与下一时间步的误差之和。
$${\delta }_h=g^{\prime }(z)V{\delta }_{out}+{\delta }_{next}$$给定这个隐藏层的全部误差项，我们可以使用链式法则计算权重 U 和 W 的梯度了。

这些梯度为我们提供了更新矩阵 U 和 W 的所需信息。不过这还没完，我们仍然需要计算前一隐藏层 $h_{t-1}$ 的误差项，以进行后续处理。也就是基于权重矩阵 U 将误差从 ${\delta }_h$ 向后传到 $h_{t-1}$。$${\delta }_{next}=g^{\prime }(z)U{\delta }_h$$到这里我们就得到了全部梯度来对三个权重矩阵进行更新了。注意，在这个简单的例子中，没有必要把误差通过 W 传递到输入 x ，因为输入的训练数据都是固定值。当然如果我们希望更新我们的输入词语或者是词嵌入，我们也可以将误差一直向后传递到它们。
总体来看，训练 RNN 中的权重是一个双线算法。第一条线，我们进行前向推理，计算 $h_t$, $y_t$，把每一个时间步的损失都加起来，保存每一个时间步的隐藏值以用于下一时间步。第二条线，我们反向处理这个序列，计算误差项梯度，计算并保存误差项以用于后向每个时间步的隐藏层。这个方法被称为 Backpropagation Through Time (BPTT)。

9.1.3 将网络展开为计算图

我们用了上面的网络展开图来说明了 RNN 的时间特性。不过，利用现代化的计算框架和充足的计算资源，显式地把循环网络展开为深度前馈计算图，对于逐词进行句子级处理非常实用。在这种方法中，我们提供了一种范式，把网络的基本结构具体化出来，包括输入层、隐藏层、输出层等的参数，权重矩阵，还有激活函数、输出函数。然后，当传入真实的输入序列，我们可以为这个输入生成一个展开的前馈网络，然后使用这个图来进行前向推理或者通过反向传播进行训练。
对于那些需要处理很长输入序列的应用，比如语音识别、字符级句子处理、或者连续输入流，把整个输入序列展开可能就不太实际。在这种情况下，我们可以把输入展开为可操作的定长片段，把每个片段作为一个单独的训练项。

9.2 循环神经网络的应用

循环神经网络被证明是非常有效的方法，尤其是在建立语言模型、词类标注等序列标注任务，还有情感分析、主题分类等分类任务上。在后面的章节中我们也会看到，RNN 为摘要、机器翻译、问答系统等 sequence-to-sequence 方法打下了基础。

9.2.1 循环神经语言模型

我们已经见过两种建立概率语言模型的方法了：N 元模型、带滑窗的前馈网络，给定上文语境，都可以预测后面的词语。准确地说，是给定上文词语，它们可以计算出下一个词语的条件概率，$P(W_n|W_1^{n-1})$ 。
在两种方法中，模型的质量大体上取决于上下文的长度以及模型对语境的有效利用。因此，两种模型都受到马尔可夫假设（也就是下面公式）的限制：
$$P(W_n|W_1^{n-1})\approx P(W_n|W_{n-N+1}^{n-1})$$也就是说，在 N 个上文词语以外的内容，对计算没有任何贡献。
循环神经语言模型处理序列时，每个时间步处理一个词语，使用当前词语和前面的隐藏状态作为输入，预测序列中的下一个词语。这样就避免了 N 元模型和前馈网络对上下文长度的限制，因为隐藏状态包含了前面所有词语的信息。
循环语言模型的前向推断与 9.1.1 中描述的一样。每个时间步，网络获取一个词语的嵌入，然后与前面时间步产生的隐藏状态加在一起计算新的隐藏状态。这个新的隐藏状态继续产生输出层，最后通过 softmax 层在全体词汇表上生成一个概率分布。$$P(W_n|W_1^{n-1})=y_n=softmax(V{h}_n)$$最后，整个序列的概率就是序列中每一项的概率的积。
$$P(w_1^n)=\prod _{k=1}^{n}P(w_k|w_1^{k-1})=\prod _{k=1}^n{y}_k$$
正如第7章中介绍的，训练这个模型我们需要具有代表性的语料库作为训练材料。任务是给定上文词语预测下一个词语，使用交叉熵作为损失函数。单个样本的交叉熵损失就是正确词语的负对数概率，也就是输出层使用 softmax 后的结果。$$L_{CE}(\hat{y},y)=-log{\hat{y}}_i=-log\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}$$这里，正确词语 $i$ 是语料中真正的下一个词语，$y_i$ 是整个词语对应的概率，softmax 是作用在整个长度为 $K$ 的词典上。网络中的权重通过最小化交叉熵损失得到调整。

神经语言模型用于生成

在第三章中我们看过概率莎士比亚生成器，使用香农(1951)的方法随机生成句子。过程如下：

• 首先使用句子开头的标记 从softmax得到的输出中选择一个词语作为第一个输入。
• 把第一个词的词嵌入输入到网络中，然后再从输出结果中得到下一个词语。
• 继续生成后续词语直到生成句子结尾标记，或者达到了句子的最大长度。
  这种技术叫做自回归生成 (autoregressive generation) ，因为每个时间步所生成的词语取决于前一个时间步所生成的词语。如下图所示，RNN 的隐藏层和循环连接细节隐藏在蓝色块中。
  
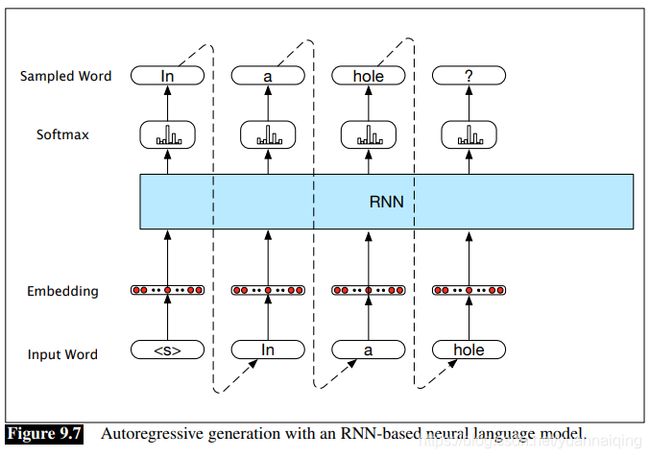
  这个结构为机器翻译、自动摘要、问答等应用启发出达到sota水平的方法。这些方法的关键是为生成组件提供合适的上下文。在第10章我们会讲编码-解码网络。
  最后，我们可以正式地评估生成文本的质量，方法是使用困惑度，对比生成的输出与训练语料库中的样本。$$PP(W)=\sqrt[N]{\prod _{i=1}^N\frac{1}{P(w_i|w_{i-1})}}$$困惑度越低，说明模型越好。

9.2.2 序列标注

在序列标记中，网络的任务是从一个固定的标签集合中选择标签，为序列中的每一个元素打上标签。一个标准的例子就是词性标注。使用 RNN 进行词性标注，输入的是词嵌入，输出的是在标签集上使用 softmax 后每个标签的概率，如下图所示。

上图中，每一个时间步的的输入是与输入词语相对应的预训练的词嵌入。其中一个展开的简单循环网络被抽象为 RNN 模块，里面包含每个时间步的输入层、隐藏层、输出层，也包括共享的 U、V、W 这些权重矩阵。网络在每一个时间步的输出为 softmax 层生成的概率在词性标签集上的分布。
为了生成一个给定输入的标签序列，我们可以在输入序列上运行前向推理，然后通过 softmax 选出每一步最有可能的标签。因为我们在输出概率分布式时使用的是 softmax，我们在训练的时候仍然使用交叉熵损失。
还有一个与序列标注紧密相关且极其有用的应用，就是在某些任务领域中发现并且标注出一段文本，命名实体识别（named entity recognition）就是其中一种，就是在文本中找到所有人名、地名、组织名称。（17章中会详解）
使用序列标注解决片段识别问题，我们将用到一个叫做 IOB编码 的技术。简单来说就是，我们用 B 来标注片段开始的词语，I 表示片段内的词语，O 表示片段之外的词语。可以参考下面这个例子：

上图中，我们感兴趣的片段就是 United、Denver、San Francisco 。
如果我们希望得到更具体的实体类别（比如找到并区分人名、组织名、地点名），我们可以把 B 和 I 更加具体化，这时候标签集的会从3个标签增长为 2*N+1 个标签，这里的 N 是类别的数量。那么上面的例子就会被重新编码为：

通过这样的编码方式，我们把片段识别任务简化成了每个词语的标注任务，输入还是常用的词嵌入，每个点的输出还是经过 softmax 计算后的标签的概率分布。
序列标注还能解决的一个问题是结构预测（structure prediction），比如输入一个序列，产生一个结构化的输出，例如一棵分析树或者意义表示。
One way to model problems like this is to learn a sequence of actions, or operators, which when executed would produce the desired structure. Therefore, instead of predicting a label for each element of an input sequence, the network is trained to select a sequence of actions, which when executed in sequence produce the desired output. The clearest example of this approach is transition-based parsing which borrows the shift-reduce paradigm from compiler construction. 以上整段不理解，第13章依存分析会讲到这个。

维特比和条件随机场(CRFs)

当我们把逻辑回归应用于词性标注，独立地为序列中的每一个元素选择一个最有可能的标签，有时候效果并不好。在 IOB 标注的例子中，甚至不能保证结果在形式上的合理性。比如，上面的方法并不能避免标注结果出现一个 I 跟在在一个 O 后面（ OI 这种情况是不合理的）。同样地，进行多分类的时候，也避免不了 I-LOC 跟在 B-PER 后面。
解决这个问题的一个方法是把循环网络的输出序列与另一个输出层语言模型结合起来，比如第8章中的。然后我们可以使用一个维特比算法的变体来选择最有可能的标签序列。这种方法通常是在循环网络的最后一层增加一个 CRF 层。

9.2.3 RNNs应用于序列分类

RNNs 的另一个用法是把整个序列进行分类。我们在第4章中讨论过情感分析。其他的还包括文档级的主题分类、垃圾邮件识别、客服系统的消息发送、欺诈检测等。在这些应用中，文本中的序列会在一个小型类别目录中被分类。
这种应用的实现方式是：把需要分类的文本逐词传入 RNN 中，每个时间步生成一个新的隐藏层，文本的最后一个词语生成最后一个隐藏状态 $h_n$，它作为整个序列压缩后的表示，然后再把它作为输入传到一个前馈网络中，最后通过 softmax 选择出最可能的类别。

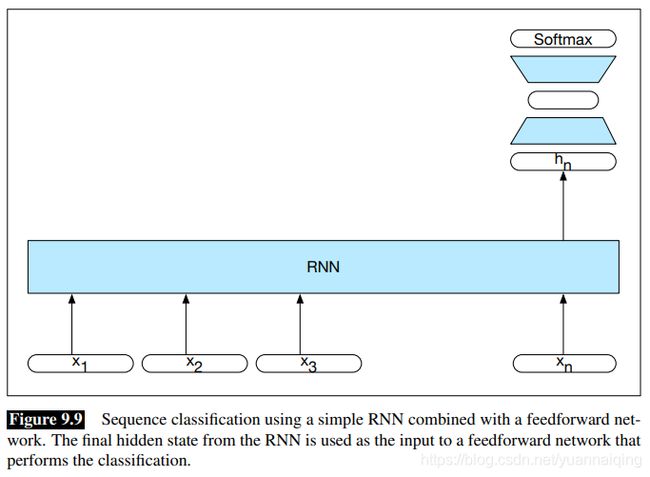
注意，在上面的方法中，在最后一个词语之前的所有词语，都没有任何的输出。因此，前面的词语没有相应的损失项。用来训练网络中权重的损失函数只与最后的文本分类任务相关。具体来说，前馈分类器的 softmax 输出加上交叉熵损失，共同驱动网络的训练。分类的误差信号反向通过前馈分类器传播到它的输入，再通过 RNN 传播到RNN的三组权重。这种把简单循环网络与前馈分类器结合的方法是我们第一个深度神经网络。这种使用使用下游应用程序的损失来调整整个网络的权重的方案，被称为端到端训练（end-to-end training）。

9.3 深度网络：堆叠与双向RNNs

从图 9.9 展示的序列分类结构可以看出，循环网络非常的灵活。把展开的计算图的前馈特性与向量化的输入输出结合起来，复杂的网络就可以看作是各类模块的创造性结合。这一部分介绍两种语言处理中更为常用的基于 RNN 的网络架构。

9.3.1 堆叠 RNNs

直到目前，我们看到的例子中 RNN 的输入是词语序列或者词嵌入，输出是一组向量，用来预测单词、标签、或者序列标注。然而，其实我们也可以把一个 RNN 的整个输出序列作为输入传到另一个 RNN 。堆叠RNNs 包含多个网络，一层的输出作为后续层的输入，如下图。

很多任务都证实堆叠 RNNs 要比单层网络效果好。一个原因是不同的网络层对表示有不同的抽象能力。正如人类的视觉系统，初期检测到边缘，然后用来发现更大的区域或形状。网络初始各层产生的表示，将作为后续层有用的抽象，而这是单层 RNN 很难做到的。
堆叠RNNs的最优数量根据具体应用和训练集不同。不过，堆叠得越多训练成本会增加相当之快。

9.3.2 双向 RNNs

在一个简单循环网络中，时刻 t 的隐藏状态表示网络截至 t 时刻对序列所知的一切。也可以说，时刻 t 的隐藏状态是截至 t 时刻的所有 input 的函数结果。我们可以把它看作是当前时刻网络左侧的语境:$$h_t^f=RN{N}_{forward}(x_1^t)$$这里 $h_t^f$ 对应 t 时刻的隐藏状态，表示目前收集到的关于序列的所有信息。
某些情况下，我们是可以同时得到整个输入序列的。我们可能会问：当前输入的右侧语境是否有用？一种获得此类信息的方法是使用反向序列作为输入训练 RNN ，使用的网络与我们之前讨论的一样。使用这种方法，时刻 t 的隐藏状态就变成了当前 input 右侧的全部序列信息：$$h_t^b=RN{N}_{backward}(x_t^n)$$这里 $h_1^n$ 表示从时刻 t 一直到序列结尾的信息。
将向前和向后两个网络结合起来就成了双向 RNN（bidirectional RNN）(Schuster,1997)。一个 Bi-RNN 包含两个独立的 RNN ：一个的 input 是从开头到结尾，一个的 input 是从结尾到开头。然后我们把两个网络的 output 结合为一个 representation，在任何一个时刻它就都捕获了当前 input 的左右全部语境。$$h_t=h_t^f\oplus h_t^b$$
下图展示了一个双向网络，把向前和向后的 outputs 直接连接起来(concatenate)。 当然将向前和向后的语境结合起来的方法包括逐个元素相加或者相乘等。每个时刻的 output 捕获到了当前 input 左右两边的信息。在序列标注应用中，这种连接 outputs 的方法可以作为局部标注的基础。

双向 RNN 也被证明是序列分类的有效方法。还记得在进行序列分类时，我们用最后的隐藏状态作为后续前馈分类器的输入，这样做的一个问题是最终隐藏状态一般会带有更多的语句后部的信息，语句前部信息较少。双向 RNN 就解决了整个问题，如下图，我们把向前网络和向后网络各自的最终状态结合起来，作为后续处理的 input 。这里直接连接（concatenation）还是常用的结合两个 outputs 的方法，不过向量内逐个元素相加、相乘或者取平均也经常用到。

9.4 RNN 中上下文的处理方法：LSTM 和 GRU

实践表明，很难训练出能充分利用与当前时刻较远的信息的 RNN。尽管可以访问整个前面的序列，隐藏状态内编码的信息往往具有局部性，也就是与最近的输入序列和状态相关。然而，很多情况下，很多语言应用中远距离信息非常关键。比如，在进行语言建模的时候有下面这个例子：
The flights the airline was cancelling were full.
在 airline 后面，模型将会给 was 一个较高的概率，因为 airline 为数的一致性提供了一个相当强的局部语境。但是，给 were 一个合理的概率就很困难了，不只因为复数 flights 非常远，而且还因为中间的语境包含单数成分。理想情况下，网络需要能够一直保留远端复数 flights 的信息直到被使用，还能够正确处理序列的中间部分。
RNN 不能有效传递关键信息的一个原因来源于隐藏层，进一步说是那些决定隐藏层值的权重，它们同时承担了两个任务：为当前决策提供有用的信息；为未来的决策传递、更新信息。
第二个训练RNN 的困难来自于通过时间来反向传递误差信号。t 时刻的隐藏层因为要参与下一时间步的计算，所以会对下一时间步的损失产生影响。 As a result, during the backward pass of training, the hidden layers are subject to repeated multiplications, as determined by the length of the sequence. 这个过程的结果是梯度会最终趋向于零，也就是所谓的梯度消失（vanishing gradients）。
为了解决这些问题，更加复杂的网络架构被设计出来，以实现随着时间保存相关上下文信息。具体来说，网络要学会忘记那些不需要的信息，记住那些能用于未来决策的信息。

9.4.1 长短期记忆（Long Short-Term Memory）

LSTM 网络（Hochreiter, 1997）把上下文管理问题分为两个子问题：移除不再需要的上下文信息、添加用于未来决策的信息。解决这两个问题的关键是学习到管理上下文的方法而不是对架构进行硬编码。LSTM 实现的方法是，首先在常规的循环隐层之外，增加一个显性的上下文层：使用特殊化的多个神经单元组成这一层，这些单元利用 “门” 来控制信息在单元内的流入和流出。这些门的实现是使用额外的权重，按顺序对 input、前一隐层、前一上下文层进行操作。
LSTM 中的门都是同样的设计：每一个都包含一个前馈层加 sigmoid 激活函数，然后与被门控的层进行点乘。选择 sigmoid 作为激活函数是希望它的输出处于0到1之间。Combining this with a pointwise multiplication has an effect similar to that of a binary mask. 被门控的层的值与近1相乘则值会没有什么变化地向后传递；值与近0相乘则会被抹掉。
第一个门被称为遗忘门（forget gate），目的是从上下文信息中删除不会用到的信息。遗忘门对前一隐藏状态和当前 input 进行加权求和，并传入 sigmoid 函数。然后结果作为 掩膜（mask）与上下文向量相乘，以移除不再需要的上下文信息。$$f_t=\sigma (U_f{h}_{t-1}+W_f{x}_t)$$$$k_t=c_{t-1}\odot f_t$$接下来是从前一隐藏状态和当前 inputs 中提取出实际的信息——这与循环网络中基本的计算一样。$$g_t=tanh(U_g{h}_{t-1}+W_g{x}_t)$$再接下来我们为 增加门（adding gate）生成一个mask，选择出信息以增加到当前上下文。$$i_t=\sigma (U_i{h}_{t-1}+W_i{x}_t)$$$$j_t=g_t\odot i_t$$然后我们把它加到修正后的上下文中。$$c_t=j_t+k_t$$最后的一个门是 输出门（output gate），用来决定当前隐藏状态需要哪些信息（而不是为未来决策保留哪些信息）。$$o_t=\sigma (U_o{h}_{t-1}+W_o{x}_t)$$$$h_t=o_t\odot tanh(c_t)$$

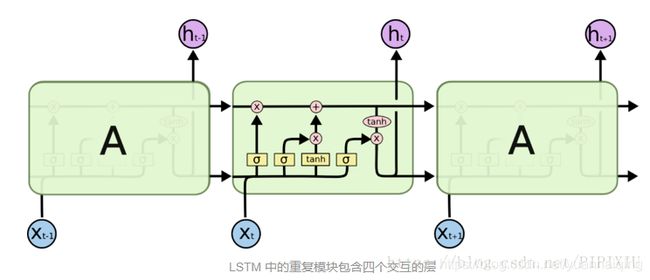
图9.13展示了 LSTM 的一个单元的完整计算。给这些门合适的权重，LSTM 把前一时间步的上下文层、隐藏层以及当前 input 作为输入。然后它生成新的上下文向量和隐藏向量作为输出。隐藏层 $h_t$ 可在堆叠的 RNN 中作为后续层的 input ，或者为网络的最后一层生成 output 。

9.4.2 Gated Recurrent Units (GRU)

LSTM 为循环网络引入了大量的额外参数，使得我们现在需要学习 8 组权重（也就是每个单元中的 4 个门都需要学习 U 和 W），而在简单的循环单元中我们只需要学习 2 组。训练这些额外的参数会大大增加训练成本。GRU（Cho，2014）不再使用独立的上下文向量，把门的数量减少到 2 ，一个 重置门 r，一个更新门 z。$$r_t=\sigma (U_r{h}_{t-1}+W_r{x}_t)$$$$z_t=\sigma (U_z{h}_{t-1}+W_z{x}_t)$$和 LSTM 中一样，在这些门的设计当中，sigmoid 的使用是得到一个二元掩膜（a binary-like mask），当值接近 0 的时候阻断信息，当值接近 1 的时候使信息流过。
重置门的目的是：决定前一隐藏状态中，哪一方面与当前语境相关，哪些可以被忽略。通过将 r 与前一隐藏状态进行元素相乘，得到一个 mask，然后用这个mask值计算 t 时刻隐藏状态的一个中间表示。$${\tilde{h}}_t=tanh(U(r_t)\odot h_{t-1}+W{x}_t)$$更新门 z 的工作是：决定这个中间表示的哪一方面会被用到新的隐藏状态中，以及前一隐藏状态的哪一方面会被保留。它的实现方式是：$$h_t=(1-z_t)h_{t-1}+z_t{\tilde{h}}_t$$

9.4.3 门控单元，层，网络

在 LSTM 和 GRU 中所用的神经单元很明显比基础的前馈网络中的要明显复杂。幸运的是，这种复杂性被封装在基本处理单元中，是我们能够保持模块化，并能轻松地尝试不同的架构。要看到这一点，图 9.14 表示出了与每种单元相关的输入和输出。

最左边的 （a）是一个基础的前馈单元，使用一组权重和一个激活函数来决定输出，层中的各单元间没有连接。（b）表示简单循环网络中的一个单元，有两个 input，还增加了一组权重，不过仍然是只有一个激活函数和一个输出。
LSTM（c）和 GRU（d）把增加的复杂性封装在了单元内。与（b）相比，LSTM 在外部提升的复杂度是增加了上下文语境向量作为 input 和 output。GRU 与简单循环网络有一样的 input 和 output 结构。
这种模块化是 LSTM 和 GRU 单元功能强大和广泛应用的关键。LSTM 和 GRU 单元可以替换 9.3 节中介绍的所有网络架构。而且，与单间的 RNN 一样，使用门控单元的多层网络可以展开为深度前馈网络，并通过常规方式使用反向传播进行训练。

9.5 词语、subwords、字符

一直到现在，我们一直假设网络的 input 是词嵌入。正如我们看到的，基于单词的嵌入非常适合捕捉单词之间的分布相似性（句法和语义）。然而，凡事就怕然而，只用基于词语的方法还是有缺陷的：

• 对于某些语言和应用，词典过大，把每一个可能的词语表示为嵌入不太实际。需要使用较小成分组成单词的方法。
• 不论词典多大，我们都会遇到未知词，因为会有新词、拼写错误、从其他语言借词。
• 单词级别以下的形态信息，是很多语言和应用的重要信息来源。基于单词的方法看不到这种规律。
• 过去几年，人们探索了多种替代基于单词的方法。下面是已经尝试过的主要方法。
• 完全忽略单词，仅使用字符序列作为 RNN 的 input。
• 使用诸如从字节对编码或语音分析中派生的 subword 作为 input。 使用成熟的形态学分析 to derive a
  linguistically motivated input sequence.
  毫无疑问，没有一个最好的方法可以适用所有的语言和应用。
  一个特别成功的方法是将词嵌入与构成单词的字符嵌入相结合。
  9.15 展示了在词性标注中一个方法。图的上部是一个 RNN，接收一个序列作为 input，并通过 softmax 输出词性标签的分布。注意这里的 RNN 可以具有任意的复杂度，可以包含堆叠的或者双向的网络层。
  这个网络的 input 包含常规的词嵌入再加上字符级的信息。特别地，每个 input 由常规的词嵌入和一个双向 RNN 产生的嵌入拼接而成，这个 RNN 接收每个单词的字符序列作为输入，如图下部所示。
  input 中每个单词的字符序列通过双向RNN运行，该RNN由两个独立的RNN组成，一个RNN从左到右处理，另一个从右到左。在 9.3.2 中我们讨论过，两个方向的 RNN 的最后隐藏状态拼接起来，来得到每个单词的复合的字符级表示。尤为重要的是，这些字符嵌入是在整个任务的背景下进行训练的，词性标注的 softmax 层的损失会一直传播回字符嵌入。
  

总结

这一章介绍了循环神经网络的概念以及如何把它们应用到语言问题。以下是对本章的重点：
在简单循环神经网络中，序列的处理是一个时间步一个元素。
一个神经单元在某一时刻的输出取决于当前的 input 和前一时间步的隐藏层值。
RNN 可以使用反向传播算法的一个扩展来训练，这个算法被称为通过时间的反向传播（BPTT）。
RNN 基于语言的常见应用包括：
概率语言建模，其中模型将概率分配给序列，或者在给定前面单词的情况下为后面元素分配概率。
使用训练好的模型进行自动回归生成。
序列标注，为序列中的每个元素打上标签，就如词性标注。
序列分类，把整个文本打上类别标签，如垃圾邮件分类、情感分析、主题分类。
Simple recurrent networks often fail since it is extremely difficult to successfully train them do to problems maintaining useful gradients over time.
更复杂的门控架构如 LSTM 和 GRU 被设计出来克服这些问题，它们可以显式地控制任务来决定在隐层和上下文层中记住或者忘记哪些信息。

文献和历史说明

关于 RNN 的较有影响力的研究是1980年代圣地亚哥大学的并行分布处理小组进行的。大部分的研究针对的是人类认知模型的构建而不是NLP应用（Rumelhart，1986）。在前馈网络的隐藏层中使用循环是Elman1990年提出的。Jordan（1986）研究了类似的架构，在output层使用了循环。Mathis（1995）在隐藏层之前增加了一个循环的上下文层。Rumelhart（1986）讨论了把循环网络展开为一个等价的前馈网络的可能性。
在认知建模工作进行的同时，人们在信号处理、语音社区等连续信号领域进行了广泛的演技（Giles，1994）.Schuster（1997）引入了双向 RNN，并且描述了TIMIT因素转录任务的结果。
训练RNN和处理长距离上下文的困难阻碍了实际应用的进展。然后LSTM的出现改变了这一困境（Hochreiter，1997）。在信号处理和语言处理的跨领域任务上，包括音素识别（Graves，2005），手写识别（Graves，2007），语音识别（Graves，2013），性能得到了巨大的提升。
Collobert（2008）等人的工作激发了人们将神经网络应用于实际NLP问题的兴趣。这些工作使用了预训练词嵌入，卷积网络，端到端训练。他们在多个标准的开放任务上实现了接近sota的性能，包括词性标注，语块、命名实体识别，语义角色标注，而无需使用人工特征工程。
将LSTM与基于word2vec（Mikolv，2013）和GLOVE（Pennington，2014）集合的方法迅速主导了很多常规任务：词性标注（Ling，2015），syntactic chunking（Sogaard，2016），使用IOB标记的命名实体识别（Chiu，2016），意见挖掘（Irsoy，2014），语义角色标注（Zhou，2015），AMR parsing（Foland，2016）。与早期设计统计机器学习的进步一样，这些进展得益于CONLL， SemEval和其他共享任务提供的训练数据，还有Ontonotes（Pradhan，2007），PropBank（Palmer，2005）提供的共享资源。