一看就懂的高级数据结构：跳表
之前我们讨论过二叉查找算法，数据是存储在数组中的，因为二分查找算法底层依赖数组按照下标快速访问元素的特性。现在我们想想，如果数据存储在链表中，就无法用二分查找算法了吗？
实际上，我们只需要对链表稍微改造，就可以支持类似“二分”的查找算法。我们把改造之后的数据结构称为跳表(skip list)。
跳表是基于有序链表，添加多级索引构建而成，支持快速的查找，插入，删除数据操作。除此之外，跳表还支持快速的查找某个区间的数据。在实际的项目开发中，Redis中的有序集合(sorted set)就是用跳表实现的。
这是关于二分查找的文章，大家可以先进行学习。二分查找
跳表的由来
对于单链表，即便链表中存储的数据是有序的，如果想要在其中查找某个数据，也只能从头到尾遍历，查找效率很低，时间复杂度为O(n)。
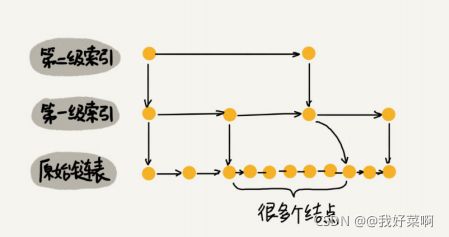
现在就要思考一个问题，怎样才能提高查找效率呢？我们对链表建立一个一级“索引”，每两个节点提取一个节点到索引层。索引层中的每个节点包含一个down指针，指向下一级节点。
假设我们要查找某个节点，比如查找上图中的16这个节点。我们首先在索引层遍历，当遍历到索引层中的13这个节点时，发现下一个节点是17，要查找的节点肯定在13到17之间，然后，我们通过13这个索引处节点的down指针，下降到原始链表这一层，继续在原始链表中遍历。此时，我们只需要再遍历两个节点就可以找到16这个节点的。所以现在，查找16这个节点原本需要遍历10个节点，现在只需要遍历7个节点就可以了。
从上面的例子可以看到，加上一层索引的时候，查找结点的数量变少了，然后速率提高了。那么，再加上一层索引，速率会不会更高呢？
与建造第一级索引的方式一样，我们在第一级索引的基础上，每两个结点抽出一个结点到第二级索引，再遍历16这个结点的话，只需要遍历6个节点，如图。
这么看可能也不太明显，我们看一个包含64个节点的链表。然后建造五层索引。
当我们查找第62个节点的时候，在原来没有索引的时候，需要遍历62个节点，现在有了五级索引，只需要遍历11个节点，所以当节点n比较大的时候，需要查询一个节点的时候，效率就会非常高。
用跳表查询到底有多快
在单链表中查询某个数据的时间复杂度为O(n),那么，在具有多级索引的跳表中，查询某个数据的时间复杂度为多少呢？
在分析之前，我们先看一个这样的问题：一个包含n个节点的链表最多会有多少级索引？
按照之前说的，每两个节点会抽出一个节点作为上一级索引的节点，粗略计算，第一级索引的节点个数大约是n/2,第二级索引的节点的个数大约是n/4，第三级索引的节点的个数是n/8，也就是说，第k级索引的节点的个数大约是第k-1级索引节点的1/2。假设索引有h级，然后加上原始链表这一层，那么整个跳表的高度约为log
N。
在跳表中查询数据时，如果每一层平均遍历m个节点，那么在跳表中查询数据的时间复杂度为O(mlogn)，，按照前面这种索引结构，每一级索引最多需要遍历3个节点，也就是m=3。
现在再来看看为什么m是3，假设要找的节点是x，如上图所示，在第k级索引中，当遍历到节点y之后，发现节点x的值大于节点y的值，小于后面z的值，于是，我们通过down指针从k级索引降低到k-1级索引，节点y到节点z之间有3个节点，索引m=3,因此，在第k-1级索引中，最多遍历三个节点，依次类推，每一级索引需要遍历3个节点。
通过上面的分析，知道了m = 3，因此，跳表中查询数据的时间复杂度为O(logn)，与二分查找的时间复制度相同，也就是说，我们通过链表实现类二分查找。
跳表是不是很浪费内存
相比于单链表，跳表需要存储多级索引，势必要消耗更多的存储空间。
其实跳表的空间复杂度并不难分析，假设原始链表大小为 n，那第一级索引大约 有 n/2 个结点，第二级索引大约有 n/4 个结点，以此类推，每上升一级就减少一半，直到 剩下 2 个结点。如果我们把每层索引的结点数写出来，就是一个等比数列。
这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以，跳表的空间复杂度是 O(n)。也就是说，如果将包含 n 个结点的单链表构造成跳表，我们需要额外再用接近 n 个 结点的存储空间。那我们有没有办法降低索引占用的内存空间呢？
上面说的是每两个节点抽取一个节点到上一级索引，那我们是不是可以抽取多个节点中的一个到上一级索引呢？
从图中可以看出，第一级索引需要大约 n/3 个结点，第二级索引需要大约 n/9 个结点。每 往上一级，索引结点个数都除以 3。为了方便计算，我们假设最高一级的索引结点个数是 1。我们把每级索引的结点个数都写下来，也是一个等比数列。
通过等比数列求和公式，总的索引结点大约就是 n/3+n/9+n/27+…+9+3+1=n/2。尽管
空间复杂度还是 O(n)，但比上面的每两个结点抽一个结点的索引构建方法，要减少了一半
的索引结点存储空间。
也就是说，我们只需要调整抽取节点的间隔，就可以控制节点占用的存储空间，以此来达到时间复杂度和空间复杂度的平衡。
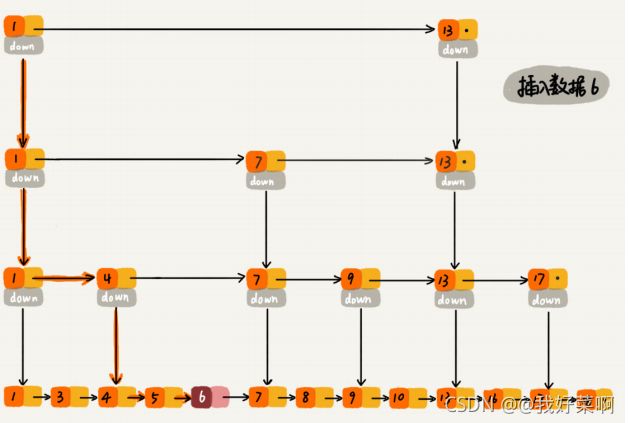
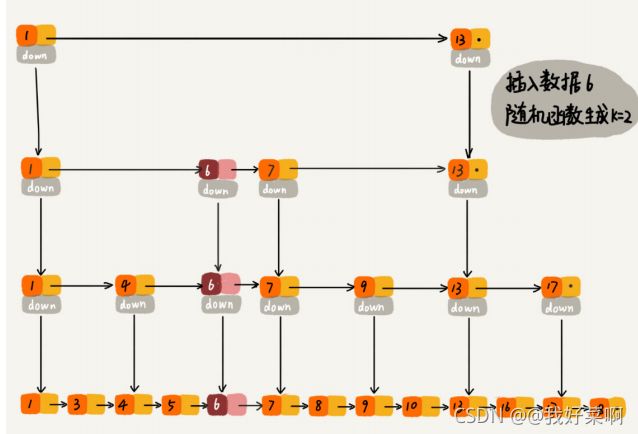
高效的插入和删除
跳表作为一个动态的数据结构，不仅支持查找操作，还支持
插入和删除，并且时间复杂度都为O(logn)。
对于单链表来说，插入一个数据需要遍历来查找插入的位置，比较耗时，但是对于跳表，就可以使用多级索引，快速找到需要插入的位置。看一下下面的图。
删除操作
如果这个结点在索引中也有出现，我们除了要删除原始链表中的结点，还要删除索引中的。
因为单链表中的删除操作需要拿到要删除结点的前驱结点，然后通过指针操作完成删除。所
以在查找要删除的结点的时候，一定要获取前驱结点。当然，如果我们用的是双向链表，就
不需要考虑这个问题了。
关于删除操作可以参考这偏文章：链表
跳表索引动态更新
当频繁的向跳表中插入数据的时候，如果插入的过程不断伴随着索引的更新，就可能导致某两个节点之间数据非常多，在极端的情况下，可能会退化为单链表。
作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说，如果链表中结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插 入、删除操作性能下降。
跳表是通过随机函数来维护前 面提到的“平衡性”。
当我们往跳表中插入数据的时候，我们可以选择同时将这个数据插入到部分索引层中。如何 选择加入哪些索引层呢？
我们通过一个随机函数，来决定将这个结点插入到哪几级索引中，比如随机函数生成了值 K，那我们就将这个结点添加到第一级到第 K 级这 K 级索引中
代码
package com.algorithms.list;
import java.util.*;
/**
* 跳表
*
* @Author: Yinjingwei
* @Date: 2019/7/9/009 21:36
* @Description:
*/
public class SkipList> implements Iterable {
//当前层数
private int curLevel;
//头结点，不保存值
private Node head;
//跳表中元素个数
private int size;
//用于生成随机层数
private static final double PROBABILITY = 0.5;
//最大层数,也可以写成通过构造函数注入的方式动态设置
private static final int maxLevel = 8;
public SkipList() {
size = 0;
curLevel = 0;
head = new Node(null);
}
public int size() {
return size;
}
public boolean add(E e) {
if (contains(e)) {
return false;
}
int level = randomLevel();
if (level > curLevel) {
curLevel = level;
}
Node newNode = new Node(e);
Node current = head;
//插入方向由上到下
while (level >= 0) {
//找到比e小的最大节点
current = findNext(e, current, level);
//将newNode插入到current后面
//newNode的next指针指向该节点的后继
newNode.forwards.add(0, current.next(level));
//该节点的next指向newNode
current.forwards.set(level, newNode);
level--;//每层都要插入
}
size++;
return true;
}
//返回给定层数中小于e的最大者
private Node findNext(E e, Node current, int level) {
Node next = current.next(level);
while (next != null) {
if (e.compareTo(next.data) < 0) {
break;
}
//到这说明e >= next.data
current = next;
next = current.next(level);
}
return current;
}
public Node find(E e) {
if (empty()) {
return null;
}
return find(e, head, curLevel);
}
private Node find(E e, Node current, int level) {
while (level >= 0) {
current = findNext(e, current, level);
level--;
}
return current;
}
public boolean empty() {
return size == 0;
}
/**
* O(logN)的删除算法
*
* @param e
* @return
*/
public boolean remove(E e) {
if (empty()) {
return false;
}
boolean removed = false;//记录是否删除
int level = curLevel;
//current用于遍历,pre指向待删除节点前一个节点
Node current = head.next(level), pre = head;
while (level >= 0) {
while (current != null) {
//e < current.data
if (e.compareTo(current.data) < 0) {
break;
}
//只有e >= current.data才需要继续
//如果e == current.data
if (e.compareTo(current.data) == 0) {
//pre指向它的后继
pre.forwards.set(level, current.next(level));
//设置删除标记
removed = true;
//跳出循环内层循环
break;
}
pre = current;
current = current.next(level);
}
//继续搜索下一层
level--;
if (level < 0) {
//防止next(-1)
break;
}
//往下一层,从pre开始往下即可，不需要从头(header)开始
current = pre.next(level);
}
if (removed) {
size--;//不要忘记size--
return true;
}
return false;
}
/**
* 生成随机层数[0,maxLevel)
* 生成的值越大，概率越小
*
* @return
*/
private int randomLevel() {
int level = 0;
while (Math.random() < PROBABILITY && level < maxLevel - 1) {
++level;
}
return level;
}
public boolean contains(E e) {
Node node = find(e);
return node != null && node.data != null && node.data.compareTo(e) == 0;
}
@Override
public Iterator iterator() {
return new SkipListIterator();
}
private class SkipListIterator implements Iterator {
Node current = head;
@Override
public boolean hasNext() {
return current.next(0) != null;
}
@Override
public E next() {
current = current.next(0);
return current.data;
}
}
private class Node {
//保存值
E data;
//保存了每一层上的节点信息，可能为null
List forwards;
Node(E data) {
this.data = data;
forwards = new ArrayList<>();
//事先把每一层都置为null，虽然空间利用率没那么高，但是简化了实现
//也可以通过自定义列表(比如B树实现中用到的Vector)来实现，就可以不用下面的操作
for (int i = 0; i <= maxLevel; i++) {
forwards.add(null);
}
}
@Override
public String toString() {
return data == null ? " " : "" + data;
}
/**
* 得到当前节点level层上的下一个(右边一个)节点
*
* @param level
* @return
*/
Node next(int level) {
return this.forwards.get(level);
}
}
public void print() {
//记录了第0层值对应的索引，从1开始
Map indexMap = new HashMap<>();
Node current = head.next(0);
int index = 1;
int maxWidth = 1;//值的最大宽度，为了格式化好看一点
while (current != null) {
int curWidth = current.data.toString().length();
if (curWidth > maxWidth) {
maxWidth = curWidth;//得到最大宽度
}
indexMap.put(current.data, index++);
current = current.next(0);
}
print(indexMap, maxWidth);
}
private void print(int level, Node current, Map indexMap, int width) {
System.out.print("Level " + level + ": ");
int preIndex = 0;//该层前一个元素的索引
while (current != null) {
//当前元素的索引
int curIndex = indexMap.get(current.data);
if (level == 0) {
//第0层直接打印即可
printSpace(curIndex - preIndex);
} else {
//其他层稍微复杂一点
//计算空格数
//相差的元素个数 + 相差的元素个数乘以宽度
int num = (curIndex - preIndex) + (curIndex - preIndex - 1) * width;
printSpace(num);
}
System.out.printf("%" + width + "s", current.data);
preIndex = curIndex;
current = current.next(level);
}
System.out.println();
}
/**
* 打印num个空格
*
* @param num
*/
private void printSpace(int num) {
for (int i = 0; i < num; i++) {
System.out.print(' ');
}
}
private void print(Map map, int width) {
//从顶层开始打印
int level = curLevel;
while (level >= 0) {
print(level, head.next(level), map, width);
level--;
}
}
public static void main(String[] args) {
//Random random = new Random();
//int[] values = random.ints(2000, 1, 10000).toArray();
int[] values = {1, 6, 9, 3, 5, 7, 4, 8};
SkipList list = new SkipList<>();
for (int value : values) {
//System.out.println("add: " + value);
list.add(value);
//list.print();
//System.out.println();
}
System.out.println("before remove:");
list.print();
System.out.println();
for (int value : values) {
list.remove(value);
System.out.println("remove: " + value);
list.print();
System.out.println();
}
}
}
跳表使用空间换时间的设计思路，通过构建多级索引来提 高查询的效率，实现了基于链表的“二分查找”。跳表是一种动态数据结构，支持快速的插 入、删除、查找操作，时间复杂度都是O(logn)。
跳表的空间复杂度是 O(n)。不过，跳表的实现非常灵活，可以通过改变索引构建策略，有 效平衡执行效率和内存消耗。虽然跳表的代码实现并不简单，但是作为一种动态数据结构， 比起红黑树来说，实现要简单多了。所以很多时候，我们为了代码的简单、易读，比起红黑 树，我们更倾向用跳表。