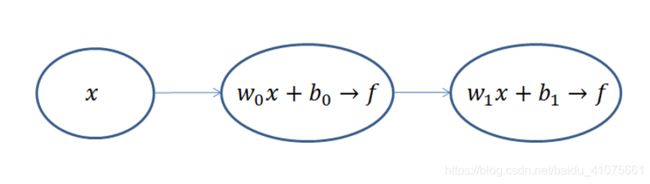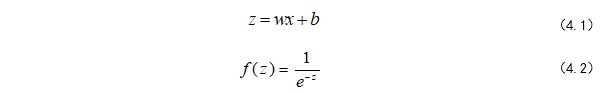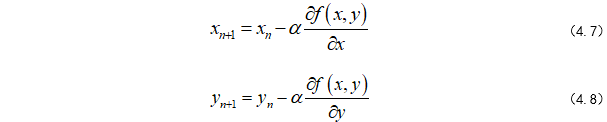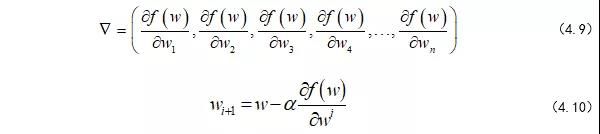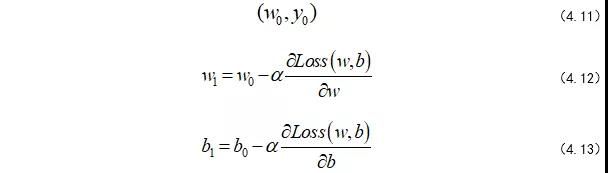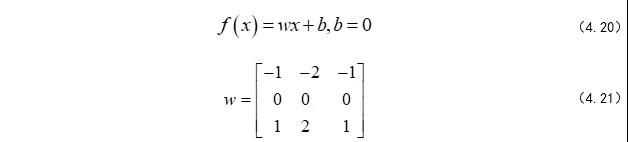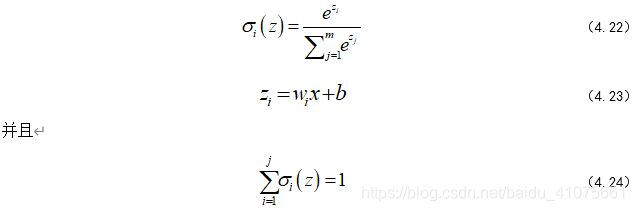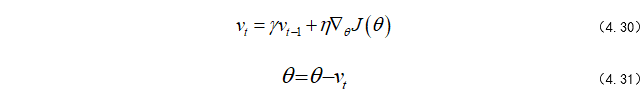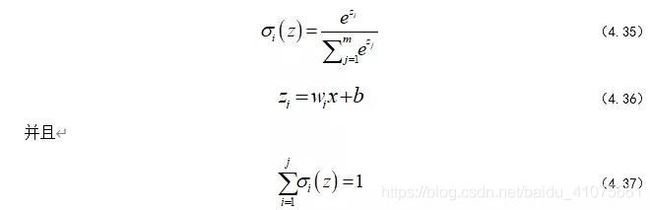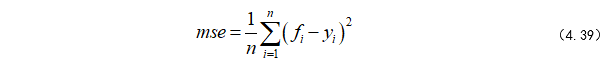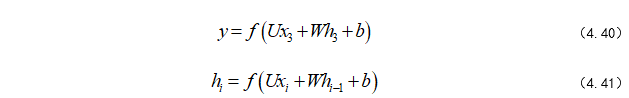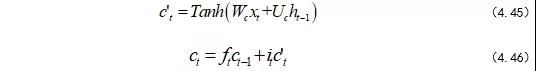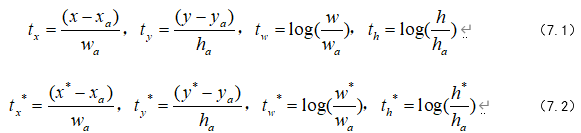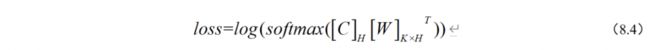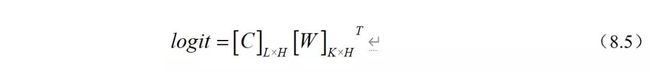机器学习-hjasfgiudgasu
1 . 基本概念
人工智能包裹着机器学习,机器学习包裹着深度学习。简单来讲,人工智能是一个概念,机器学习是实现人工智能的一种方法,而深度学习是实现机器学习的一种技术。(图- 1.2)
人工智能:顾名思义就是人工赋予机器智能,但与人工智能先驱们所设想的赋予机器独立思考能力的“强人工智能”所不一样,目前我们所说的人工智能都是“弱人工智能”。它能跟人一样实现一些既定的任务,例如人脸识别、垃圾邮件分类等,有时甚至可以超越人类。
深度学习:则是人们通过仿生学创造性提出的一种人工神经网络技术。人们通过训练这些神经网络,使其出色地完成了很多机器学习任务。因此,深度学习是人工智能历史上一个重大突破,它拓展了人工智能的领域范围和促进了人工智能的发展。深度学习模型执行的任务可以归为两类:分类任务和回归(预测)任务
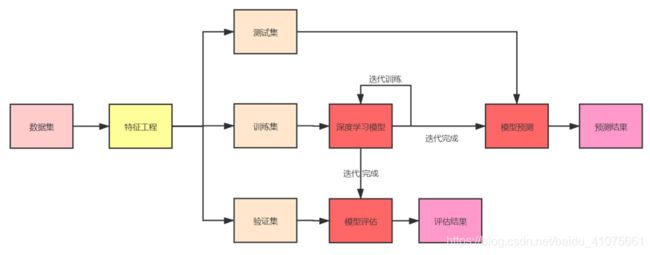
1.1 深度学习算法流程
训练集用以训练深度学习模型;验证集用以评估模型结果,进而辅助模型调参;测试集用以模型的预测。一般而言,训练集、验证集与测试集的比例为7:2:1
特征工程: 提取和归纳特征,让算法最大程度地利用数据,从而得到更好的结果。
1.1.1 模型评估
1. 分类任务评估指标:
1】准确率(accuracy):对于给定数据集的预测结果,分类正确的样本数占总样本数的百分比。但是对于不均衡的训练集来说,这就会有致命的缺陷,因为当负样本占比在99%时,模型只要将结果都预测为负样本,准确率就达到了99%。在这种情况下,利用准确率对模型进行评估并不是最合理的评估方式。
2】精确率(precision)和召回率(recall rate):
-
它们是一对衡量检索系统的指标。精确率衡量的是检索系统推送出来的真实正确结果(TP)与系统推送出来的所有正确结果(TP+FP)的占比。
-
召回率衡量的是系统推送出来的*真实正确结果(TP)与整个系统的实际正确结果(TP+FN)**的占比。
但精确率和召回率是矛盾统一的一对指标,为了提高精确率,模型需要更有“把握”把真正的正样本识别出来,这样必然会放弃一些没有“把握”(但实际是正样本)的正样本,从而导致召回率降低。
eg:TP是正类样本中被分类器预测为正类的数目,FN是正类样本中被分类器预测为负类的数目,FP是负类样本中被分类器预测为正类的数目,TN是负类样本中被分类器预测为负类的数目。(表-1.1)
3】F1Score和ROC曲线
-
F1Score是精确率和召回率的调和平均值:(式-1.4-1.5)
-
ROC曲线(Receiver Operating Characteristic):一开始用于心理学、医学检测应用,此后被引入机器学习领域,用以评估模型泛化性能好坏。ROC曲线的线下面积(AUC)越大,也意味着该模型的泛化性能越好。
-
绘制ROC曲线:真阳率TPR作为纵坐标,表示正样本中被分类器预测正类的数目与总正样本数目之比;假阳率FPR作为横坐标,表示负类样本中被分类器预测为正类的数目与总负样本数目之比。(式-1.4-1.5)
eg:这里介绍一个简单绘制ROC曲线的方法:
① 根据标签统计出正负样本的数目,正样本数目记为P,负样本数目记为N;
② 其次,横轴刻度记为1/N,纵轴刻度记为1/P;
③ 接着,将模型预测的概率从大到小进行排序;
④ 最后,从零点开始,依次遍历排序好的概率,遇到正样本则纵轴刻度上升1/P,遇到负样本则横轴刻度右移1/N,直至便利完所有样本,最终停在点(1,1)上,至此,ROC曲线绘制完成
它的线下面积AUC一般在0.5~1,若小于0.5,直接将模型的预测概率反转为1-P,然后重新计算AUC即可。AUC 越大,说明分类器越稳健,将真正的正类样本放在前面的能力越强。一般地,很多机器学习任务的数据集并不是均衡的,例如诈骗信息分类,诈骗信息和正常信息之间的占比有时能会到1:1000。为了能更好地衡量我们模型的有效性,我们应该选择ROC曲线和F1Score作为评估指标。因为它们能够无视样本不均衡的情况,并根据预测结果给出最合理的评估。(图-1.4ROC曲线图)
2. 分类任务评估指标
回归是确定两种或两种以上的变量间相互依赖的定量关系的方法,简单来讲就是对自变量X和因变量Y建立函数关系式。为了评估这个函数关系式的有效性,我们可以通过以下几个评估指标来衡量。其中,fi为模型预测值,yi为实际值。(式-1.6-1.8)
对于给定数据集的预测结果,分类正确的样本数占总样本数的百分比。但是对于不均衡的训练集来说,这就会有致命的缺陷,因为当负样本占比在99%时,模型只要将结果都预测为负样本,准确率就达到了99%。在这种情况下,利用准确率对模型进行评估并不是最合理的评估方式。
4. 深度学习
4.1 Keras神经网络框架
优点:
1. 允许简单快速的原型设计(用户友好性,模块化和可扩展性)。
2. 支持卷积网络和循环网络,以及两者的组合。
3. 在CPU和GPU上无缝运行。
缺点:
Keras比较注重网络层次,然而并非所有网络都是层层堆叠的,后面笔者的深度学习代码会涉及 遗传算法与神经网 络,这种网络就不是特别的规整,因此Keras在设计新的网络方面会比Tensorflow差一些。因此本书一些比较简单的 实验均由keras完成,而一些高阶实验,我们则通过Tensorflow去完成。
安装:
# GPU版本
conda install keras-gpu
# CPU版本
conda install keras
4.2 全连接神经网络
不算输入层,上面的网络结构总共有两层,隐藏层和输出层,它们“圆圈”里的计算都是公式(4.1)和(4.2)的计算组合:(式-4.1 4.2)
每一级都是利用前一级的输出做输入,再经过圆圈内的组合计算,输出到下一级。
加上f(z)这个运算的目的是为了将输出的值域压缩到(0,1),也就是所谓的归一化,因为每一级输出的值都将作为下一级的输入,只有将输入归一化了,才会避免某个输入无穷大,导致其他输入无效,变成“一家之言”,最终网络训练效果非常不好。
(图-4.4)
神经网络的训练是有监督的学习,也就是输入X 有着与之对应的真实值Y ,神经网络的输出Y 与真实值Y 之间的损失Loss 就是网络反向传播的东西。整个网络的训练过程就是不断缩小损失Loss 的过程。为此,就像高中一样,我们为了求解某个问题,列出了一个方程,如公式(式-4.3 4.5)

上述的公式经过化简,我们可以看到A、B、C、D、E、F都是常系数,未知数就是w 和b ,也就是为了让Loss 最小,我们要求解出最佳的w 和b 。这时我们稍微想象一下,如果这是个二维空间,那么我们相当于要找一条曲线,让它与坐标轴上所有样本点距离最小。比如这样,如图所示。
(图-4.5)
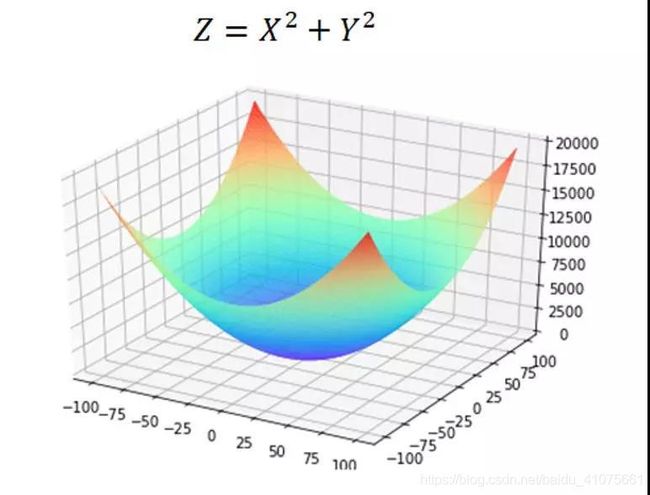
同理,我们可以将Loss 方程转化为一个三维图像求最优解的过程。三维图像就像一个“碗”,如图 4.6所示,它和二维空间的抛物线一样,存在极值,那我们只要将极值求出,那就保证了我们能求出最优的(w , b)也就是这个“碗底”的坐标,使Loss 最小。(图-4.6)
求极值,首先求导。二元凸函数使用偏导数来求导,也就是对X,Y分别求导,在求导过程中,把其他的未知量当成常数即可。
想象自己在一座山上,要想从山上最快地去到谷底,那就要沿着最陡峭的地方往下走。这个最陡峭的地方,我们叫做梯度,像不像我们对上面那个“碗”做切线,找出最陡的那条切线,事实上我们做的就是这个,求偏导就是这么一个过程。(式-4.6)
我们每走一步,坐标就会更新:(式-4.7-4.8)
当然,这是三维空间中的,假如我们在多维空间漫步呢,其实也是一样的,也就是对各个维度求偏导,更新自己的坐标。(式-4.9 4.10)
其中,w的上标i表示第几个w,下标n表示第几步,α是学习率,后面会介绍α的作用。所以,我们可以将整个求解过程看做下山(求偏导过程),为此,我们先初始化自己的初始位置。(式-4.11-4.13)
这样我们不断地往下走(迭代),当我们逐渐接近山底的时候,每次更新的步伐也就越来越小,损失值也就越来越小,直到达到某个阈值或迭代次数时,停止训练,这样找到 就是我们要求的解。
我们将整个求解过程称为梯度下降求解法。
这里还需要补充的是为什么要有学习率α,以及如何选择学习率α?
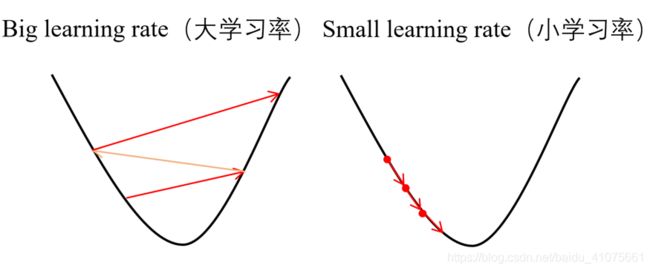
通常来说,学习率是可以随意设置,你可以根据过去的经验或书本资料选择一个最佳值,或凭直觉估计一个合适值,一般在(0,1)之间。这样做可行,但并非永远可行。事实上选择学习率是一件比较困难的事,图 4.7显示了应用不同学习率后出现的各类情况,其中epoch为使用训练集全部样本训练一次的单位,loss表示损失。(图-4.7)
可以发现,学习率直接影响我们的模型能够以多快的速度收敛到局部最小值(也就是达到最好的精度)。一般来说,学习率越大,神经网络学习速度越快。如果学习率太小,网络很可能会陷入局部最优;但是如果太大,超过了极值,损失就会停止下降,在某一位置反复震荡。
也就是说,如果我们选择了一个合适的学习率,我们不仅可以在更短的时间内训练好模型,还可以节省各种运算资源的花费。
如何选择?业界并没有特别硬性的定论,总的来说就是试出来的,看哪个学习率能让Loss收敛得更快,Loss最小,就选哪个。
4.3 CNN卷积神经网络
输入层(Input layer)、卷积层(convolutional layer)、池化层(pooling layer)和输出层(全连接层+softmax layer)
卷积神经网络与全连接神经网络的区别:
-
总有至少1个的卷积层,用以提取特征。
-
卷积层级之间的神经元是局部连接和权值共享,这样的设计大大减少了(w , b)的数量,加快了训练。
CNN整个训练过程和全连接神经网络差不多,甚至是笔者之后介绍的RNN、LSTM模型,他们的训练过程也和全连接神经网络差不多,唯一不同的就是损失Loss 函数的定义,之后就是不断训练,找出最优的(w , b),完成建模,所以大家搞懂了全连接神经网络的训练过程,就基本吃遍了整个深度学习最重要的数学核心知识了。
卷积层
(Convolutional Layer)
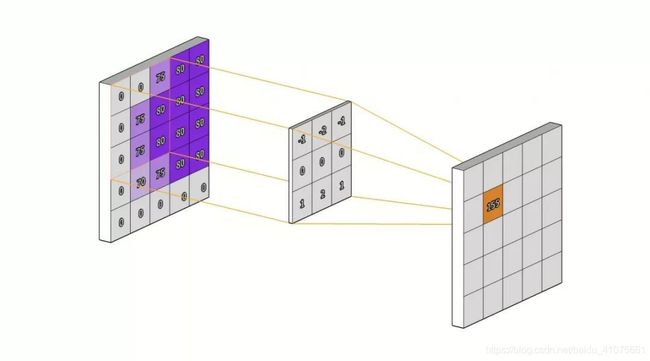
图像拥有很多冗余的信息,而且往往作为输入信息,它的矩阵又非常大,利用全连接神经网络去训练的话,计算量非常大。那么卷积层就是用来去除冗余取出精华部分,通俗易懂来说就是压缩提纯。图 (4.9)的CNN网络结构图中。卷积层里面有个小框框,那个是卷积核(Convolutional Kernel),主要通过它来实现压缩提纯的工作。
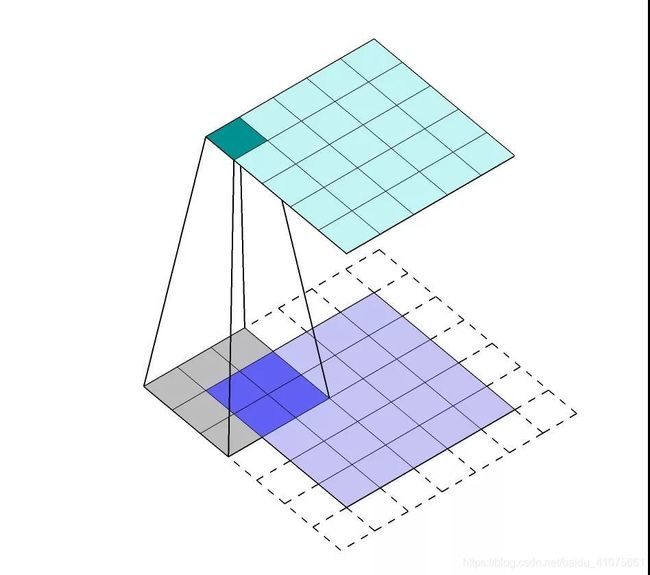
卷积核是怎么工作的?我们可以把蓝色矩阵看做卷积层的上一层,绿色矩阵看做卷积层,在蓝色矩阵上蠕动的便是卷积核,卷积核通过与他所覆盖蓝色矩阵的一部分进行卷积运算,然后把结果映射到绿色矩阵中。(4.10)
特征提取:卷积核是如何将结果映射到卷积层的(4.11)
卷积核在滑动过程中做的卷积运算就是卷积核w 与其所覆盖的区域的数进行点积,最后将结果映射到卷积层。具体的运算公式如(式-4.20 4.21)
这样看来,我们将9个点的信息量,压缩成了1个点,也就是有损压缩,这个过程我们也可以认为是特征提取。公式中(w , b)和之前全连接神经网络并没有区别,就是权值w 和偏置b ,它们在初始化之后,随着整个训练过程一轮又一轮的迭代逐渐趋向于最优。
在卷积核 之后一般会加一个Relu的激励函数,就跟全连接神经网络的神经元计算组合公式(4.1)和(4.2)一样,只不过这里换成了Relu激励函数,而全连接神经网络用的是sigmod激励函数。这么做的目的都是让训练结果更优。
好了,讲到这,大家应该大致明白了卷积层的工作方式,就是个压缩提纯的过程,而且每个卷积层不单止一个卷积核,它是可以多个的,大家又可以看一下图 4.9的CNN网络的卷积层,大家会看到输出的特征图在“变胖”,因为特征图的上一级经过多个卷积核压缩提纯,每个卷积核对应一层,多层叠加当然会“变胖”。
局部连接和权值共享
全连接神经网络的局限性中其他的网络层与层之间是全连接的,这就导致了整个训练过程要更新多对(w , b),为此CNN特定引入了局部连接和权值共享的两个特性,来减少训练的计算量。
图像或者语言亦或者文本都是冗余信息特别多的东西,倘若我们依照全连接神经网络那般全连接,也就是将所有信息的权值都考虑进了训练过程。卷积就是适当得放弃一些连接(局部连接),不仅可以避免网络将冗余信息都学习进来,同时也和权值共享特性一样减少训练的参数,加快整个网络的收敛。
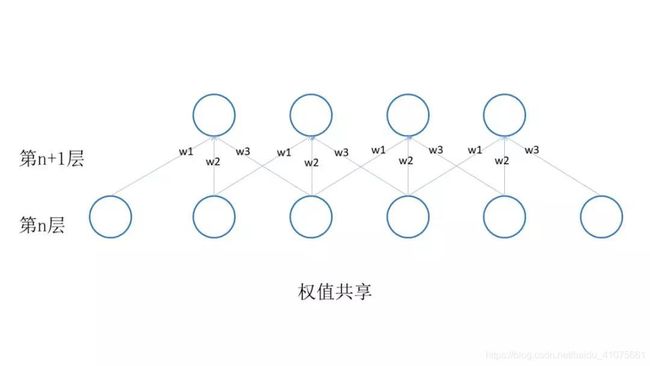
局部连接与权值共享如图 4.12和图 4.13所示。(图-4.12)
(图-4.13)
重点看权值共享这张图,它同时也采用了局部连接,总共就有3*4=12个权值,再加上权值共享,我们就只用求3个权值了,大大减少了我们的计算量。
池化层
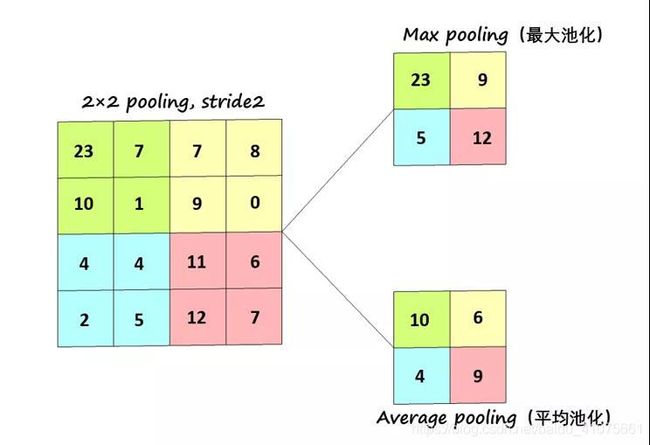
(Pooling Layer)(图-4.14)
max就是将对应方块中最大值一一映射到最大池化层(max pooling layer)
mean就是将对应方块的平均值一一映射到平均池化层(mean pooling layer)
整个CNN架构就是一个不断压缩提纯的过程,目的不单止是为了加快训练速度,同时也是为了放弃冗余信息,避免将没必要的特征都学习进来,保证训练模型的泛化性。
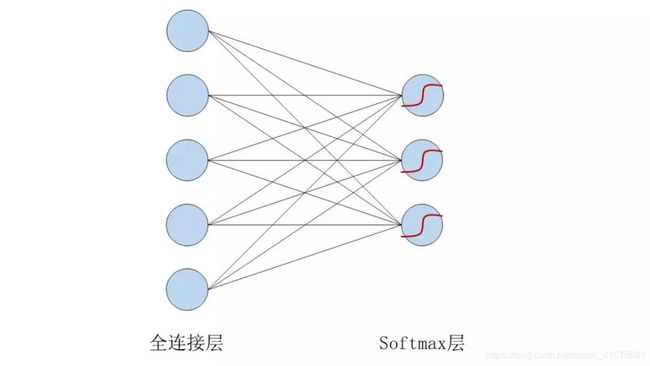
输出层
softmax
CNN损失函数之所以不同也是因为它,这层是CNN的分类层,如图 4.15所示(4.15)
softmax层的每一个节点的激励函数(式-4.22-4.24)
上面的公式,我们可以理解为每个节点输出一个概率,所有节点的概率加和等于1,这也是CNN选择softmax层进行分类的原因所在,可以将一张待分类的图片放进模型,softmax输出的概率中,最大概率所对应的标签便是这张待分类图的标签。
这时候,笔者给大家举个例子就明白了。现在我们的softmax层有3个神经元,也就是说我们可以训练一个分三类的分类器,现在假设我们有一组带标签的训练样本,他们的标签可以如此标记,对应节点标记1,其他标记0。其实就是onehot编码,如图 4.16所示。(4.16)
训练的时候将训练样本图片放入输入层,标签向量放入输出层,最终训练出一个模型。此时,笔者将一张待分类的图片放入我们的模型中,如果最后softmax层输出的结果是结果(图-4.25)。
0.85对应着最大概率,说明这张图片是猫。接着所有概率加起来等于1,这样是不是好理解很多啦。好了,讲了这么久,我们还是没有把softmax的损失函数给写出来,它有点特殊,叫交叉熵,如式(4.26)~(4.27)
虽说它长得奇奇怪怪的,但是整体的训练过程和全连接神经网络的思路是一样,都是通过梯度下降法找出最优的(w , b),使Loss 最小,最终完成建模。
####CNN的超参数设置
1. 卷积核初始化
卷积核的权值w和偏置b一开始是需要我们人工去初始化的,这里初始化的方法有很多。Tensorflow或者Keras在我们构建卷积层的时候自行给我们初始化了,但是哪天大家心血来潮想自己初始化也是可以的,我们的权值初始化可以根据高斯分布去设置,这样得到的初始化权值更加符合自然规律,毕竟咱们的计算机也是自然界的一部分。
2. Padding
Padding是指对输入图像用多少个像素去填充,如(图-4.17)
这么做的目的也非常的简单,就是为了保持边界信息,倘若不填充,边界信息被卷积核扫描的次数远比不是中间信息的扫描次数,这样就降低了边界信息的参考价值了。
其次还有另外一个目的是,有可能输入图片的尺寸参差不齐,通过Padding来使所有的输入图像尺寸一致,避免训练过程中没必要的错误
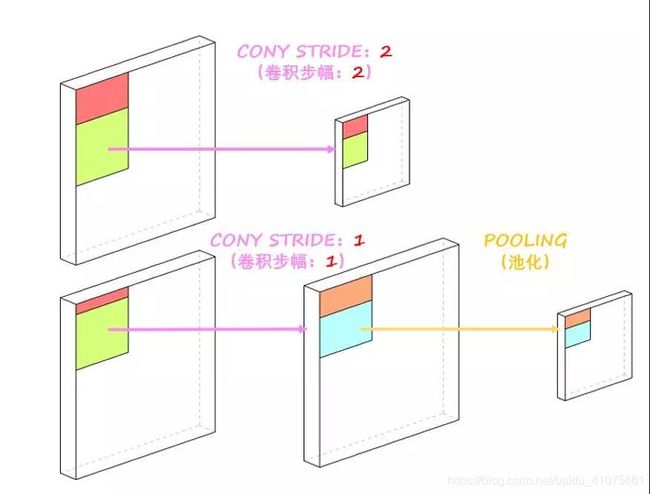
**3. Stride步幅 **
就是卷积核工作的时候,每次滑动的格子数,默认是1,但是也可以自行设置,步幅越大,扫描次数越少,得到的特征也就越“粗糙”,至于如何设置,业界并没有很好的判断方法,也就是说,一切全靠大家自己去试,怎么优秀怎么来。如图 4.18所示。
4.4 超参数
(Hyperparameters)
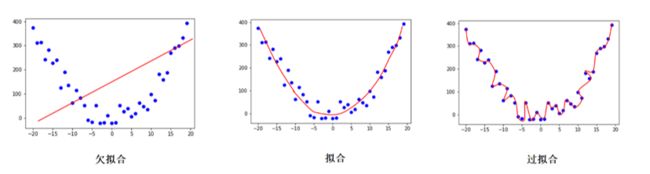
4.4.1 过拟合
-
过拟合:过于相似。简单的例子,大家一般在考试前都会通过做题来复习,假如我们当晚做的题都在第二天考场上见到了,那么咱们的分数就会高很多,但是其实出别的题目,大家可能就答不上来了,这时候我们就把这种情况叫过拟合,因为大家只是记住了一些题目的特征,但是并没有很好地了解题目最本质的真理。
-
泛化性:适用广泛。简单的例子,泛化就像学神考试,不管他当晚有没有复习到第二天考试的题目,依旧能拿高分,因为学神已经将所有题目最本质的真理都学会了,所以不管出什么题目他都能通过已经掌握的真理去解答,这就是泛化。
1. 正则化
正则化的目的就是为了模型的泛化而添加的一个权值累加项。正则化有好几种,这里笔者主要介绍L1与L2两种正则化,其他正则化与它们只是形式上有所区别,但它们的数学核心思想都是一样的。说到正则化,难免逃不开数学公式,L1与L2正则化的公式如式(4.28)~(4.29)所示。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LWGGMpBP-1604662143442)(C:\Users\Jing\OneDrive\笔记\机器学习\图包\式-4.28 4.29.png)]
好了,这时候我们先认识一下公式里面的参数,由之前Loss(C0)和这个权值累加项组成。C就是当前神经网络的损失,C0与就是之前提及的损失 Loss,重点是权值累加项a/n ∑w|w| 。
我们又可以看下公式了,公式有个对权重的累加部分,那我们设想下权重越大,越多,那损失C越大,权值越多,越大说明我们花费了很多时间和精力去记住某个题目的特征,而忽略了题目本身的真理。现在加入这一个权值累加项,就是为了让我们时时刻刻在计算自己的损失,我们知道神经 网络的训练是通过梯度下降不断减小损失C的过程,那么加上这一项就可以有“意识”地避开增大w的方向去行走。
那我们可以将式子中的a理解为惩罚因子。如果我们对下面这个部分越重视,那我们就加大a,迫使它向权值w减小的方向快速移动。
L1和L2的区别。L1是绝对值,L2是平方,以此类推可以知道L3、L4等等正则项也是这么来的。L2前面加的那个1/2只是为了求导的时候好约分,可以说算是一个计算技巧。附上一个对比图,如图 4.20所示,让大家对两个正则化公式有个直观的了解。(图-4.20)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ddpn3wLW-1604662143443)(C:\Users\Jing\OneDrive\笔记\机器学习\图包\图-4.20.png)]
在只考虑二维情况下,我们在(w1, w2)的权值平面上可视化代价函数Loss的求解过程,圆心为样本值,半径是误差,红色的边界是正则项的约束条件(权值累加项),两者相交则是整个代价函数Loss的最优解。可以将整个求解的过程理解为在让w1、w2最小的情况下,让样本与正则项(L1 或者 L2的权值累加项)相交得到最优解。
我们可以看到的是L2比较圆润(二次项),L1则是方块比较尖(一次绝对值),这样L2与样本相交的时候,最优解(w1, w2)都是有值的,而L1与样本相交得到的最优解(w1, w2)其中w1=0。所以,L1倾向于更少的特征,其他特征为0,而L2倾向于更多的特征,每个特征都有值。这只是二维情况下,如果在三维甚至更高维度,大家也可以想象L1为棱角分明的尖物体,而L2为圆润的物体,这样他们与高维的样本相交的时候,生成的最优解也和二维情况一样。而且本质上也符合上面正则化项(权值累加项)的约束:尽可能让权值更小与更少,这样我们得到模型泛化性越强。
2. Dropout
正则化只是让权值w变小,并没有让权值w的数量减少,因为当整个网络结构确定下来的时候,权值w的数量就已经确定了,而正则化并不能去改变网络结构。这时候Dropout就登场了,我们在每一轮训练过程中随机放弃一些神经元节点,这样我们一定程度上就相当于减少了权值数量,用更少的权值数量去训练网络,相当于我们用最高效的方法去掌握多的题目,本质上就是加强模型泛化性的过程。依惯例,这里附上一个Dropout示意图,如图 4.21所示
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hKGLcTFG-1604662143444)(C:\Users\Jing\OneDrive\笔记\机器学习\图包\图-4.21.jpg)]
4.4.2 优化器
大家了解到了整个网络的训练都是基于梯度下降法去训练的,但是当数据量多的时候,梯度下降法训练就会非常的慢,因为我们每一轮训练都会对所有数据求梯度。为此,有一些人就对梯度下降提出了优化方法,也就是笔者即将介绍的优化器。
1. 随机梯度下降
Stochastic Gradient Decent(SGD)
梯度下降法每次训练都用全部样本,然而这些计算是冗余的,因为我们每次都用同样的样本去计算。而随机梯度下降法(SGD)为此做了些许改变,每次只选择一个样本来更新来更新梯度,这样学习速度肯定非常的快,并且支持对新的数据进行在线更新,如图 4.22所示。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qQQGEKua-1604662143444)(C:\Users\Jing\OneDrive\笔记\机器学习\图包\图-4.22.png)]
当然了,我们为了速度快,理所应当的要付出一些代价,不像梯度下降法那样每次更新都会朝着Loss不断减小的方向去移动,最后收敛于极值点(凸函数收敛于全局极值点,非凸函数可能会收敛于局部极值点),SGD由于每次选择样本的随机性,会有些许波动,也就是上图的SGD收敛示意图,走的路会比较曲折,有时候会从一个点突然跳到另外一个点去,不过这样也有好处,因为对于非凸Loss函数,我们用梯度下降法很可能收敛在在局部极值点就不动了,但是SGD却能用它的随机选择样本更新梯度的特性跳出局部极值点,很可能在非凸Loss函数中找到全局极值点。
#####2 . 动量
Momentum
我们知道了SGD的缺点,为了解决它的波动性,有人在SGD的基础上又添加了点东西,从而抑制SGD的震荡。这个东西就是动量,我们先看下Momentum的公式如(4.30)~(4.31)所示。(式-4.30 4.31)
我们通过添加γv(t-1)这项,让随机梯度下降拥有了动量,这时候大家要回忆一下高中物理了,动量是具有惯性的,也就是我们在下山过程中,即使随机走路,但是受限于惯性,我们不可能随便跳来跳去,从而抑制了SGD在梯度下降过程中震荡,为此笔者在这附上一张图,如图 4.23所示,让大家有个更直观的理解。(图-4.23)

从图 4.24我们就可以看出,加入了动量抑制了震荡,走的路至少不这么曲折了,这个方法就是Momentum。
3. RMSprop
熟悉TensorFlow或者Keras调参的读者可能会觉得学习率(Learning Rate)调参是个比较麻烦的事,为此,自适应的学习率调参方法就出现了,目的是为了减少人工调参的次数(只是减少次数,还是需要人工设定学习率的)。RMSprop就是其中一个比较优秀的自适应学习率方法,如(式-4.32 4.33)所示:
RMSprop使用的是指数加权平均,旨在消除梯度下降中的摆动,与Momentum的效果一样,某一维度的导数比较大,则指数加权平均就大,某一维度的导数比较小,则其指数加权平均就小,这样就保证了各维度导数都在一个量级,进而减少了摆动。允许使用一个更大的学习率η。
4. (Adam)
Adaptive Moment Estimation
现在我们讲最后一个优化器:Adam优化器:它相当于RMSprop + Momentum,也就是拥有了这两者的优点,因此笔者在很多优秀的论文都能看到它被用来做神经网络的优化器。所以,如果不知道如何选择优化器,那就选Adam优化器吧!
4.4.3 学习率
(Learning Rate)
有些细心的读者会发现笔者在之前的全连接神经网络章节中已经提及了学习率,这里再一次提及只是为了让整个超参数知识体系更加的完整,避免大家知一不知二。首先梯度下降更新权值如(式-4.34)所示。
我们知道整个训练过程就是梯度下降更新权值的过程,对于学习率的作用,大家可以通过上面的公式以及图 4.25可以明白,对于凸函数,大的学习率可能会在学习过程中跳过全局极值点,小的虽然速度慢但是最终能收敛到全局极值点,求得最优解。图 4.24 不同学习率的梯度下降(4.24 )
但是对于非凸函数,它可能存在许多局部最小值,大家使用较小的学习率去训练的时候,很可能让整个网络收敛于局部最小值而不是全局最小值,从而得不到最优解。可能有些读者还不了解什么是非凸函数。如图 4.25所示,它就是存在局部最低点的一个函数,但局部最低点并不一定是全局最低点。图 4.25 非凸函数(图-4.25)
说到这,那我们应该怎么去选择学习率呢?目前业界并没有很好的方法,大家可以通过自己调参去将学习率调到最优即可。
4.4.4 常见的激励函数
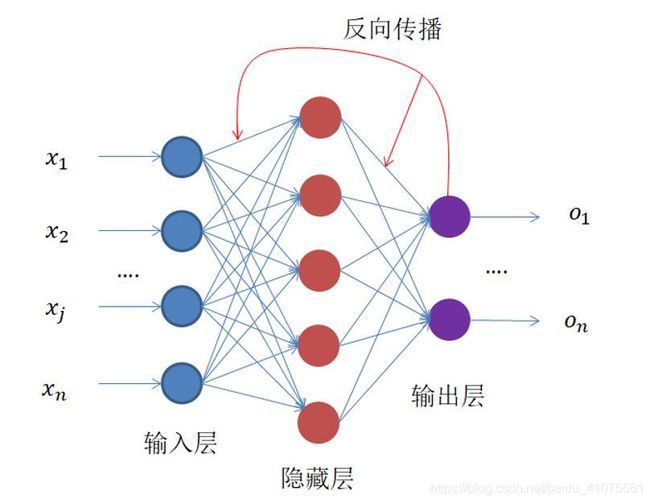
在谈及常见的激励函数前,我们得先知道激励函数是干什么用的。如(图-4.3)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uA04CWfW-1604662143449)(C:\Users\Jing\OneDrive\笔记\机器学习\图包\图-4.3.png)]
(图4.28 )
在这里插入图片描述
2. Linear激励函数
线性激活函数,即不对神经元的输出值进行处理,直接输出。通常用在回归模型的输出层中。
3. Softmax激励函数
Softmax示意图如图 4.29所示,通常用在分类模型的输出层中。原理如下:Softmax层示意图(图 4.29 )
softmax层的每一个节点的激励函数
(式-4.35 - 式-4.37)
上面的公式,我们可以理解为每个节点输出一个概率,所有节点的概率加和等于1,这也是CNN选择softmax层进行分类的原因所在,可以将一张待分类的图片放进模型,softmax输出的概率中,最大概率所对应的标签便是这张待分类图的标签。这时候,笔者给大家举个例子就明白啦。现在我们的softmax层有3个神经元,也就是说我们可以训练一个分三类的分类器,现在假设我们有一组带标签的训练样本,他们的标签可以如此标记,对应节点标记1,其他标记0。其实就是onehot编码,如(图-4.16)
训练的时候将训练样本图片放入输入层,标签向量放入输出层,最终训练出一个模型。此时,笔者将一张待分类的图片放入我们的模型中,如果最后softmax层输出的结果是(式-4.38)。
这时,大家就明白了上诉公式的含义了,0.85对应着最大概率,说明这张图片是猫,所有概率加起来等于1,这样是不是好理解很多啦。
4. Relu激励函数
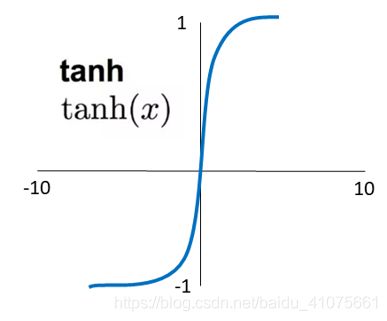
上面提到sigmoid和tanh激励函数容易导致多层神经网络模型在训练过程中出现梯度消失的现象。为此,如图 4.30所示,有人提出了Relu激励函数来弥补它们的不足之处,因此Relu函数及其变种(leaky relu 、pre relu等)经常放在多层神经网络的中间层。
且Relu函数的计算速度比sigmoid和tanh快。从下图可知,relu函数只需要判断神经元的输出值是否小于0,然后输出相应的值即可,因此整体网络的收敛速度会比较快。Relu激励函数(图-4.30)
4.4.5 常见的损失函数
同样地, 在谈及损失函数之前,我们先复习下整个神经网络的训练过程。它是基于梯度下降的方法去不断缩小预测值与真实值之间差值的过程。而这个差值就是损失(loss),计算这个损失的函数就是损失函数(loss function)了。且损失函数是和神经网络输出层的激励函数相配套的。接下来笔者将根据我们训练的任务来讲解常见的损失函数。
1. 回归任务
损失函数(loss function):mse
输出层配套激励函数:linear, sigmoid, tanh
输出层神经元个数:1个
均方误差mse如公式(4.39)所示:
其中,f是模型预测值,y_i是实际值,通过计算两者的均方误差来衡量模型的有效性。
2. 二分类任务
(1)损失函数:binary_crossentropy
输出层配套激励函数:softmax
输出层神经元个数:2个
(2)损失函数:binary_crossentropy
输出层配套激励函数:sigmoid or tanh
输出层神经元个数:1个
这个损失函数(二分类交叉熵)要求训练样本标签必须为独热编码(one hot encode),拟合损失的过程在上文有写,这里就不赘述了。
3. 多分类任务
(1)损失函数:categorical_crossentropy
输出层配套激励函数:softmax
输出层神经元个数:几分类便对应几个神经元
这个损失函数(多分类交叉熵)要求训练样本标签(label)必须为独热编码(one hot encode),拟合损失的过程在上文有写,这里就不赘述了。
(2)损失函数:sparse_categorical_crossentropy
输出层配套激励函数:softmax
输出层神经元个数:几分类便对应几个神经元
这个损失函数与(多分类交叉熵)相同,不过要求训练样本标签(label)必须为数字编码,如(图- 4.31)
4.4.6 其他超参数
epoch:训练模型的迭代次数。我们主要看损失是否收敛在一个稳定值,若收敛则当前设置的epoch为最佳。
BatchSize:我们用来更新梯度的批数据大小。一般来说,Batch Size设置的不能太大也不能太小,一般为几十或者几百。笔者的调参经验是看GPU占用率。我们在命令行输入gpustat查看GPU占用率,如图 4.32所示。Batch Size越大,GPU占用率也就越高,一般占满整个GPU卡训练模型为最佳。业界传闻使用2的幂次可以发挥更佳的性能,笔者并没有尝试过,大家可以去尝试一下。GPU占用率(图-4.32)
如果需要,大家可以去keras或者TensorFlow官网查看更多的参数含义与用途,不过笔者在这建议大家在需要的时候去翻阅一下即可,因为不可能把所有函数都记住的。
4.5 自编码器
自己训练自己
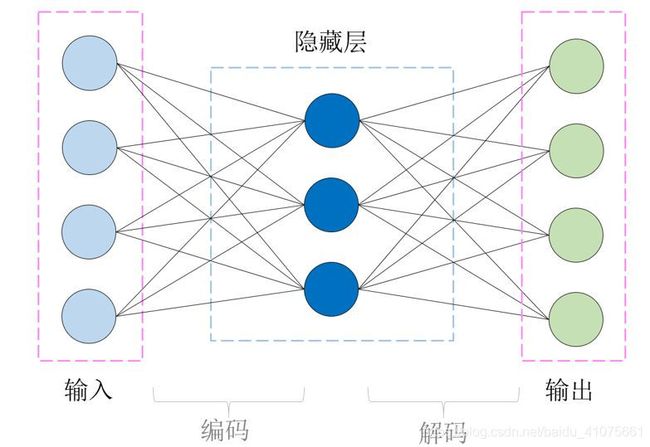
自编码器是一种输入等于输出的神经网络模型,可能大家会疑惑为什么要训练一个这样的模型,毕竟输入等于输出在大家看来就是一件多此一举的事情。一个简单的全连接神经网络自编码器模型如图 4.33
4.5.1 自编码器的原理
全连接层神经网络组成的最简单的自编码器只有三层结构,中间的隐藏层才是我们所需要关注的地方,以隐藏层为界限,左边为编码器(encoder),右边为解码器(decoder),所以在训练过程中,输入才能在经过编码后再解码,还原成原来的模样。
对传统机器学习有所了解的读者应该都知道PCA(主成分分析),它是用来对数据进行降维的。不了解PCA的读者也没关系,我们现在学习的自编码器也有这个功能,所以学完之后再看PCA兴许会理解地更加深刻些。
现在我们看回图 4.33,假如我们通过一组数据训练出了我们的自编码器,然后我们拆掉自编码器的解码器(decoder),就可以用剩下的编码器(encoder)来表征我们的数据了。隐藏层的神经元数目远低于输入层,那么就相当于我们用更少的特征(神经元)去表征我们的输入数据,从而达到降维压缩的功能。接着,我们在文章开头提到过自编码器还有降噪的功能,那它是如何实现这个功能的呢?在此之前笔者先给大家介绍下这期使用的数据集----minist手写体,这是keras自带的数据集,如图 4.34所示。
这个数据集就是手写数字0~9的图像集合,图 4.37第一行就是加噪后的手写体数据集,第二行则是原本的手写体数据集。我们把加噪后的数据集当成输入,原本的数据集当做输出,训练一个自编码器,让它在训练过程中学习数据的规律,从而把噪声去掉。这就是笔者所说的去噪功能。
4.5.2 常见的自编码器
1. 普通自编码器:就是本节开头讲的最简单的自编码器。
2. 多层自编码器
多个全连接神经网络隐藏层组成自编码器。如图 4.35所示。
**3. 卷积自编码器:**由CNN卷积神经网络组成的自编码器。用卷积层替换全连接层的原因也很简单,传统自编码器一般使用的是全连接层,对于一维信号并没有什么影响,但是对于二维图像或视频信号,全连接层会损失空间信息,而通过卷积操作,卷积自编码器能很好的保留二维信号的空间信息。卷积自编码器如图 4.36所示。
4. 正则自编码器:稀疏自编码器:稀疏自编码器就是普通自编码器的隐藏层加一个L1正则项,也就是一个训练惩罚项,这样我们训练出的编码器(encoder)表征的特征更加的稀疏,从而能得到少且有用的特征项。这也是为啥用L1正则项而不用L2正则项的原因。至于L1,L2正则项的原理,笔者已经在4.4小节中提及,在此就不再赘述。
降噪自编码器:降噪自编码器就是输入换成了加噪的数据集,输出用原数据集去训练的自编码器,目的是习得降噪功能。
4.6 RNN循环神经网络
RNN循环神经网络(Recurrent Neural Networks)与RNN结构变种LSTM长短期记忆网络(Long-Short Term Memory Networks)和GRU门控循环单元(Gated Recurrent Neural Network)。
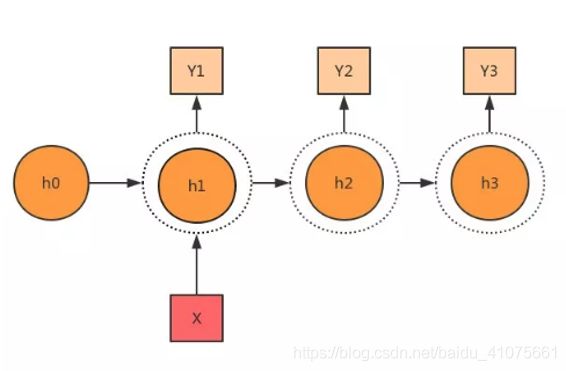
RNN与全连接神经网络的区别:同样地,我们首先来对比简单的全连接神经网络和RNN的结构有啥异同,如图4.40和图4.3所示,我们会发现RNN比全连接神经网络多了参数h0,因此RNN的神经元公式会比全连接神经网络的神经元多一项(f为激励函数),至于训练过程,和全连接神经网络并没有区别,都是是基于梯度下降的方法去不断缩小预测值与真实值之间差值的过程。如图4.37所示。
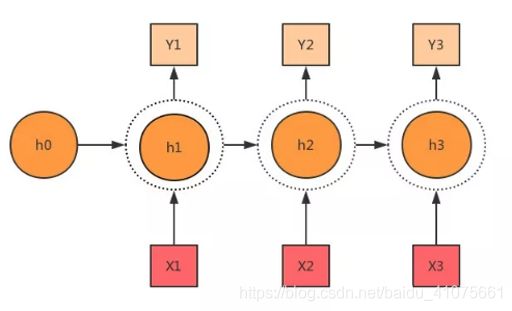
上面只是演示了简单的RNN结构,它的隐藏层h与输出y相同,我们常用的RNN结构当然不会这么简单,因此我们对上面的RNN结构进一步的拓展,如图 4.38所示。这是一个经典的多输入单输出的结构。
此时输出层的神经元公式为:(式-4.40 4.41)
由结构和公式可知,整一个RNN结构共享1组(U, W, b),这是RNN结构最重要的特性,且每一个隐藏层神经元h的计算公式是由当前输入X与上一个隐藏层神经元的输出组成。这里为了方便起见,笔者只是画了序列长度为3的RNN结构,大家可以按照这样的结构,可以将整个RNN结构无限扩大,最后接一个分类输出层或者回归输出层即可。
RNN循环神经网络的优势:我们可以看到上面的RNN结构,输入是可以多个且有序的,它可以模拟人类阅读的顺序去读取文本或者别的序列化数据,且通过隐藏层神经元的编码,上一个隐藏层神经元的信息可以传递到下一个隐藏层神经元,因而形成一定的记忆能力,能够更好地理解序列化数据。
4.6.1 其他RNN循环神经网络结构:
上面这个RNN结构最经典的用途是文本(序列)分类。当然了,RNN不止这种结构,大家可以按照自己的想法去设计输入和输出,从而完成相应的任务,接下来笔者就给大家介绍几种常见的RNN结构与其用途。
1. 单输入多输出的RNN结构:这种结构通常应用于输入一个图像,输出描述该图像的文本。如单输入多输出的·1RNN结构(图-4.39)
2. 多输入多输出的RNN结构:由于输入与输出等长,这种结构的用途就比较狭窄,仅限于输入与输出等长的序列数据如诗词文等,作诗机器人就是这么诞生的,多输入多输出如:(图-4.41)
3. 输入输出不等长的多输入多输出的RNN结构(Seq2Seq模型):
在4.4节我们已经提及了自编码器的概念,自编码器的原理可以简单理解为输入等于输出的神经网络模型。简单的全连接神经网络自编码器示意(图 4.42)
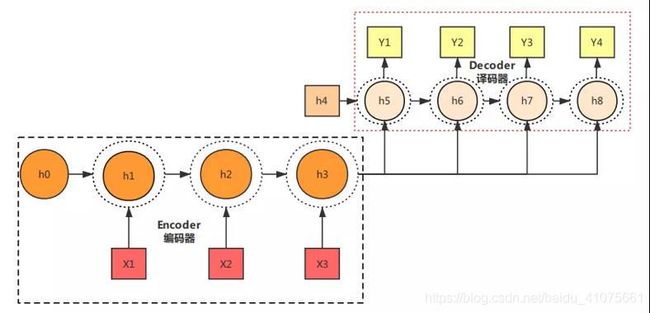
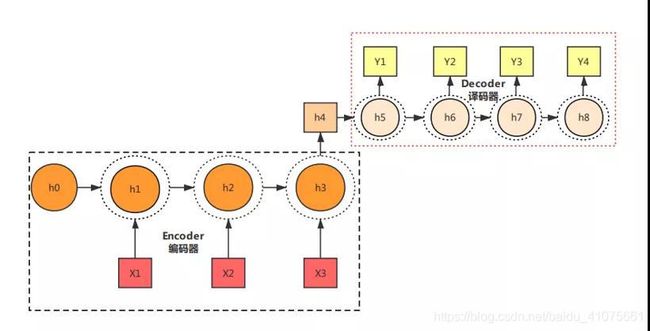
这次的主角当然不是全连接神经网络,我们只是利用RNN和自编码器的原理构造一个翻译机器人,同样的,这个自编码器(翻译机器人)的输入也等于输出,只不过输入与输出用不同的语言去表示。当然了,这个结构也可以用来完成文章摘要提取或者语音转换文字等任务。这种RNN模型业界称为Seq2Seq模型。如图 4.43和图 4.44所示
图 4.44 Seq2Seq结构形式2
4. 注意力机制下的Seq2Seq模型:上面我们提到了Seq2Seq模型可以完成机器翻译等任务,但我们从它的结构可以看出,解码器decoder的输入都是译码器encoder的同一个输出,也就是说不过输入的语句是什么,编码器encoder都会将它转换成同一个中间语义h’。
而我们知道的是每一句话都有其侧重点,那翻译当然也应该注意其侧重点,不应该是每一个词在一个句子中都具有同等地位,这样翻译出来的句子肯定效果不佳。所以,有人为此提出了注意力机制(Attention Mechanism),让我们在使用Seq2Seq的过程中,加入注意力机制,聚焦重点,提升模型效果。下面笔者以机器翻译为例子,让大家对注意力机制有更加直观的认识。
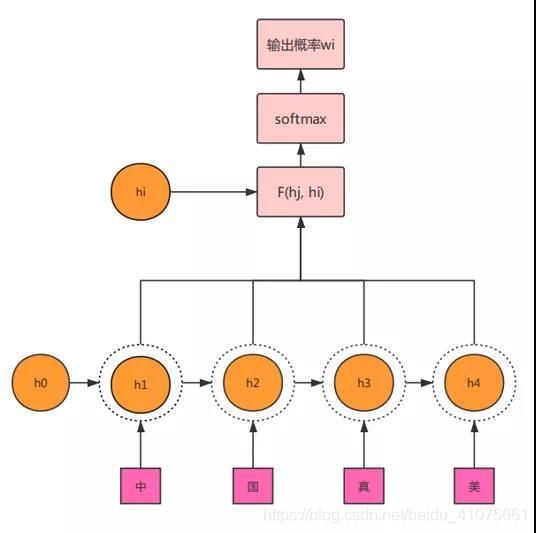
如图 4.45 注意力机制下的Seq2Seq模型的输入与输出是等长的,和前面笔者介绍的多输入多输出的RNN结构一样,只是输入变了,输入不是直接的序列输入,而是经过编码器encoder转换的中间语义C,而这些输入C也各不相同,每一个C都是由权重w和译码器的隐藏层输出h加权组成,如图 4.46
注意力模型(解码器Decoder)(图-4.45)
中间语义转换示意图(图-4.46 )
在解码器decoder部分,中间语义C1,C2,C3之间的权值表征是不同的,这也就是我们所说的注意力机制。换言之,随着训练过程的进行,重点一直在变化,而这些变化则由上图的权重w去表示,当训练停止时,权重值也就确定下来了,此时的权重值是最拟合当前训练数据的。比如C1的重点在‘中’这个字,那么中间语义可以表示为C1=0.6h_1 + 0.2h_2 + 0.1h_3 + 0.1h_4 (权值可以看成概率,所有权值值加起来为1)。因此中间语义的转换公式如式(4.42)所示
其中n为输入序列的长度。此时,我们唯一要解决的是,如何去求中间语义C的权值w表征。这就涉及到注意力模型的另一部分(编码器Encoder),如图 4.47所示。F函数和softmax函数,大家可以理解为我们要计算当前的hi与全部h(包括hi)之间的差别,从而计算出在i时刻下,每一个h对应的权值(即概率)。换言之,大家可以将下图看成分类问题,与hi越相近的,输出的概率也就越大。(图-4.47)
4.6.2 LSTM长短期记忆网络
在4.6.1提过RNN结构共享1组(U, W, b),这是RNN结构最重要的特性,不过也是由于这个特性,才导致了LSTM长短期记忆网络的诞生。因为 在(U, W, b)不变的情况下,梯度在反向传播过程中,不断连乘,数值不是越来越大就是越来越小,这样就出现了梯度爆炸或梯度消失的情况,所以往往用RNN去训练模型得不到预期的效果。
1. LSTM原理
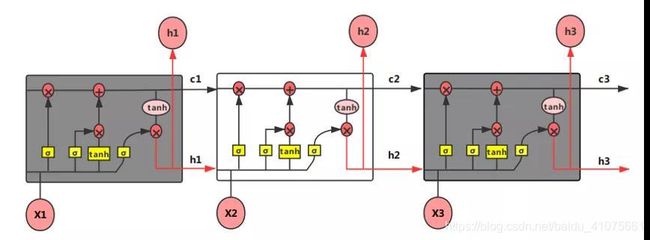
由上文可知,RNN结构之所以出现梯度爆炸或者梯度消失,最本质的原因是因为梯度在传递过程中存在极大数量的连乘,为此有人提出了LSTM模型,它可以对有价值的信息进行记忆,放弃冗余记忆,从而减小学习难度。与RNN相比,LSTM的神经元还是基于输入X和上一级的隐藏层输出h来计算,只不过内部结构变了,也就是神经元的运算公式变了,而外部结构并没有任何变化,因此上面提及的RNN各种结构都能用LSTM来替换。相对于RNN,LSTM的神经元加入了输入门i、遗忘门f、输出门o 和内部记忆单元c。笔者这里先给上一个整体的LSTM结构图如图 4.48所示,之后笔者再对它内部结构的运算逻辑进行详细的解释。 LSTM结构图(图-4.48)
遗忘门f:控制输入X和上一层隐藏层输出h被遗忘的程度大小,如图所示。遗忘门(forget gate)(图- 4.49)
遗忘门公式如式(4.43):
输入门 i:控制输入X和当前计算的状态更新到记忆单元的程度大小,如图 4.50所示。

遗忘门公式如式(4.44):
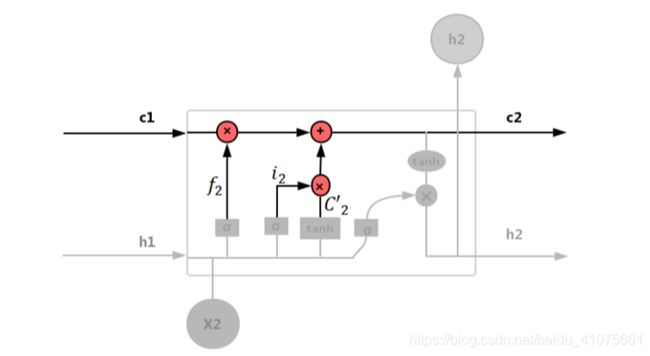
内部记忆单元 c:内部记忆单元(图-4.51)
内部记忆单元公式如式(4.45)~(4.46):
输出门 o:控制输入X和当前输出取决于当前记忆单元的程度大小,如图 4.52所示。
输出门公式如式(4.47)~(4.48):
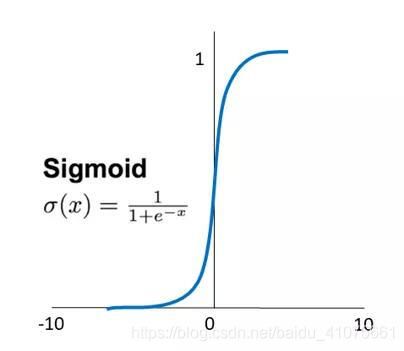
其中σ一般选择Sigmoid作为激励函数,主要是起到门控作用。因为Sigmoid函数的输出为01,当输出接近0或1时,符合物理意义上的关与开。tanh函数作为生成候选记忆C的选项,因为其输出为-11,符合大多数场景下的0中心的特征分布,且梯度(求导)在接近0处,收敛速度比sigmoid函数要快,这也是选择它的另外一个原因。不过LSTM的激励函数也不是一成不变的,大家可以根据自己的需求去更改,只要能更好地解决自己的问题即可。对于一个训练好的LSTM模型,我们要知道它的每一个门(遗忘门、输出门和输入门)都有各自的(U, W, b),上述公式也有所体现,这是在训练过程中得到的。而且当输入的序列不存在有用信息时,遗忘门f的值就会接近1,那么输入门i的值接近0,这样过去有用的信息就会被保存。当输入的序列存在重要信息时,遗忘门f的值就会接近0,那么输入门i的值接近1,此时LSTM模型遗忘过去的记忆,记录重要记忆。
因此我们可以看出由遗忘门、输出门、输入门和内部记忆单元共同控制LSTM输出h的设计,使得整个网络更好地把握序列信息之间的关系。
4.6.3 门控循环单元
(gated recurrent unit, GRU)
4.6.2节我们了解了LSTM的原理,但大家会觉得LSTM门控网络结构过于复杂与冗余。为此,Cho、van Merrienboer、 Bahdanau和Bengio[1]在2014年提出了GRU门控循环单元,这个结构如图 4.53所示,是对LSTM的一种改进。它将遗忘门和输入门合并成更新门,同时将记忆单元与隐藏层合并成了重置门,进而让整个结构运算变得更加简化且性能得以增强。GRU门控循环单元(图-4.53)
当重置门接近于0时,隐藏状态被迫忽略先前的隐藏状态,仅用当前输入进行复位。这有效地使隐藏状态可以丢弃将来以后发现不相关的任何信息,从而允许更紧凑的表示。另一方面,更新门控制从前一个隐藏状态将有多少信息转移到当前隐藏状态。这类似于LSTM网络 中的记忆单元,并有助于RNN记住长期信息。由于每个隐藏单元都有单独的重置和更新门,因此每个隐藏单元将学会捕获不同时间范围内的依赖关系。那些学会捕获短期依赖关系的单元将倾向于重置门,而那些捕获长期依赖关系的单元将倾向于更新门。而且大量的实验证明,GRU在结构上比LSTM简单,参数更少,但在实践中与LSTM的性能却没有明显的差距,甚至可能在某些任务上性能更好,因此也是当前较为流行的一种RNN变种结构。(式-4.49 - 4.52)
5. 生成对抗生成网络
5.1 生成对抗网络的原理
相信大家都会画画,不管画得好坏与否吧,但总归会对着图案勾上两笔。当我们临摹的次数越多,我们画的也就越像。最后,临摹到了极致,我们的画就和临摹的那副画一模一样了,以至于专家也无法分清到底哪幅画是赝品。好了,在这个例子中,我们将主人公换成生成对抗网络,画画这个操作换成训练,其实也是这么一回事。总体来说,就是此网络学习数据分布的规律,然后弄出一个和原先数据分布规律相似的数据。这个数据可以是语音、文字和图像等等
生成对抗网络Gan网络结构拥有两个部分,一个是生成器(generator),另一个是辨别器(discriminator)。现在我们拿手写数字图片来举个例子。我们希望Gan能临摹出和手写数字图片一样的图,达到以假乱真的程度。生成对抗网络结构图生成对抗网络(图-5.1)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vhJlwdck-1604662143474)(C:\Users\Jing\OneDrive\笔记\机器学习\图包\图-5.1.jpg)]
那么它整体的流程如下:
-
首先定义一个生成器(generator),输入一组随机噪声向量(最好符合常见的分布,一般的数据分布都呈现常见分布规律),输出为一个图片。
-
定义一个辨别器(discriminator),用它来判断图片是否为训练集中的图片,是为真,否为假。
-
当辨别器无法分辨真假,即判别概率为0.5时,停止训练。
其中,生成器和辨别器就是我们要搭建的神经网络模型,可以是CNN、RNN或者全连接神经网络等,只要能完成任务即可。
5.2 生成对抗网络的训练
- 初始化生成器G和辨别器D两个网络的参数。
- 从训练集抽取n个样本,以及生成器利用定义的噪声分布生成n个样本。固定生成器G,训练辨别器D,使其尽可能区分真假。
- 循环更新k次辨别器D之后,更新1次生成器G,使辨别器尽可能区分不了真假。
多次更新迭代后,理想状态下,最终辨别器D无法区分图片到底是来自真实的训练样本集合,还是来自生成器G生成的样本即可,此时辨别的概率为0.5,完成训练。
5.2.1 模型样本的可视化
尝试用这个框架分别对MNIST[5], the Toronto Face Database (TFD)[6], and CIFAR-10[7]. 训练了4个生成对抗网络模型。如图 5.2~图 5.5所示。样本是公平的随机抽签,并非精心挑选。最右边的列显示了模型预测生成的示例。
图-5.2 MNIST数据集
![]()
图-5.3 the Toronto Face Database数据集
图-5.4 CIFAR-10 (全连接层网络)
图-5.5 CIFAR-10 (卷积辨别器和反卷积生成器)
# chapter5/5_3_GAN.ipynb
import random
import numpy as np
from keras.layers import Input
from keras.layers.core import Reshape,Dense,Dropout,Activation,Flatten
from keras.layers.advanced_activations import LeakyReLU
from keras.layers.convolutional import Convolution2D, MaxPooling2D, ZeroPadding2D, Deconv2D, UpSampling2D
from keras.regularizers import *
from keras.layers.normalization import *
from keras.optimizers import *
from keras.datasets import mnist
import matplotlib.pyplot as plt
from keras.models import Model
from tqdm import tqdm
from IPython import display
#读取数据集
img_rows, img_cols = 28, 28
# 1. 数据集的切分与混洗(shuffle)
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(X_train.shape[0], 1, img_rows, img_cols)
X_test = X_test.reshape(X_test.shape[0], 1, img_rows, img_cols)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
print(np.min(X_train), np.max(X_train))
print('X_train shape:', X_train.shape)
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
#2. 超参数设置
shp = X_train.shape[1:]
dropout_rate = 0.25
# 优化器
opt = Adam(lr=1e-4)
dopt = Adam(lr=1e-5)
#3. 定义生成器
K.set_image_dim_ordering('th') # 用theano的图片输入顺序
# 生成1 * 28 * 28的图片
nch = 200
g_input = Input(shape=[100])
H = Dense(nch*14*14, kernel_initializer='glorot_normal')(g_input)
H = BatchNormalization()(H)
H = Activation('relu')(H)
H = Reshape( [nch, 14, 14] )(H) # 转成200 * 14 * 14
H = UpSampling2D(size=(2, 2))(H)
H = Convolution2D(100, (3, 3), padding="same", kernel_initializer='glorot_normal')(H)
H = BatchNormalization()(H)
H = Activation('relu')(H)
H = Convolution2D(50, (3, 3), padding="same", kernel_initializer='glorot_normal')(H)
H = BatchNormalization()(H)
H = Activation('relu')(H)
H = Convolution2D(1, (1, 1), padding="same", kernel_initializer='glorot_normal')(H)
g_V = Activation('sigmoid')(H)
generator = Model(g_input,g_V)
generator.compile(loss='binary_crossentropy', optimizer=opt)
generator.summary()
# 4. 定义辨别器
# 辨别是否来自真实训练集
d_input = Input(shape=shp)
H = Convolution2D(256, (5, 5), activation="relu", strides=(2, 2), padding="same")(d_input)
H = LeakyReLU(0.2)(H)
H = Dropout(dropout_rate)(H)
H = Convolution2D(512, (5, 5), activation="relu", strides=(2, 2), padding="same")(H)
H = LeakyReLU(0.2)(H)
H = Dropout(dropout_rate)(H)
H = Flatten()(H)
H = Dense(256)(H)
H = LeakyReLU(0.2)(H)
H = Dropout(dropout_rate)(H)
d_V = Dense(2,activation='softmax')(H)
discriminator = Model(d_input,d_V)
discriminator.compile(loss='categorical_crossentropy', optimizer=dopt)
discriminator.summary()
# 5. 构造生成对抗网络
# 冷冻训练层
def make_trainable(net, val):
net.trainable = val
for l in net.layers:
l.trainable = val
make_trainable(discriminator, False)
# 构造GAN
gan_input = Input(shape=[100])
H = generator(gan_input)
gan_V = discriminator(H)
GAN = Model(gan_input, gan_V)
GAN.compile(loss='categorical_crossentropy', optimizer=opt)
GAN.summary()
# 6. 训练
# 描绘损失收敛过程
def plot_loss(losses):
display.clear_output(wait=True)
display.display(plt.gcf())
plt.figure(figsize=(10,8))
plt.plot(losses["d"], label='discriminitive loss')
plt.plot(losses["g"], label='generative loss')
plt.legend()
plt.show()
# 描绘生成器生成图像
def plot_gen(n_ex=16,dim=(4,4), figsize=(10,10) ):
noise = np.random.uniform(0,1,size=[n_ex,100])
generated_images = generator.predict(noise)
plt.figure(figsize=figsize)
for i in range(generated_images.shape[0]):
plt.subplot(dim[0],dim[1],i+1)
img = generated_images[i,0,:,:]
plt.imshow(img)
plt.axis('off')
plt.tight_layout()
plt.show()
# 抽取训练集样本
ntrain = 10000
trainidx = random.sample(range(0,X_train.shape[0]), ntrain)
XT = X_train[trainidx,:,:,:]
# 预训练辨别器
noise_gen = np.random.uniform(0,1,size=[XT.shape[0],100])
generated_images = generator.predict(noise_gen) # 生成器产生样本
X = np.concatenate((XT, generated_images))
n = XT.shape[0]
y = np.zeros([2*n,2]) # 构造辨别器标签 one-hot encode
y[:n,1] = 1
y[n:,0] = 1
make_trainable(discriminator,True)
discriminator.fit(X,y, epochs=1, batch_size=32)
y_hat = discriminator.predict(X)
# 计算辨别器的准确率
y_hat_idx = np.argmax(y_hat,axis=1)
y_idx = np.argmax(y,axis=1)
diff = y_idx-y_hat_idx
n_total = y.shape[0]
n_right = (diff==0).sum()
print( "(%d of %d) right" % (n_right, n_total))
def train_for_n(nb_epoch=5000, plt_frq=25,BATCH_SIZE=32):
for e in tqdm(range(nb_epoch)):
# 生成器生成样本
image_batch = X_train[np.random.randint(0,X_train.shape[0],size=BATCH_SIZE),:,:,:]
noise_gen = np.random.uniform(0,1,size=[BATCH_SIZE,100])
generated_images = generator.predict(noise_gen)
# 训练辨别器
X = np.concatenate((image_batch, generated_images))
y = np.zeros([2*BATCH_SIZE,2])
y[0:BATCH_SIZE,1] = 1
y[BATCH_SIZE:,0] = 1
# 存储辨别器损失loss
make_trainable(discriminator,True)
d_loss = discriminator.train_on_batch(X,y)
losses["d"].append(d_loss)
# 生成器生成样本
noise_tr = np.random.uniform(0,1,size=[BATCH_SIZE,100])
y2 = np.zeros([BATCH_SIZE,2])
y2[:,1] = 1
# 存储生成器损失loss
make_trainable(discriminator,False) # 辨别器的训练关掉
g_loss = GAN.train_on_batch(noise_tr, y2)
losses["g"].append(g_loss)
# 更新损失loss图
if e%plt_frq == plt_frq-1:
plot_loss(losses)
plot_gen()
train_for_n(nb_epoch=1000, plt_frq=10,BATCH_SIZE=128)
从模型输出的loss我们可以知道生成器与辨别器两者拟合的loss并不是特别地好,因此我们可以通过调参来解决。主要调参方向有以下四点:
- batch size
- adam优化器的learning rate
- 迭代次数nb_epoch
- 生成器generator和辨别器discriminator的网络结构
无监督学习
【李宏毅深度学习】meta learning
https://zhuanlan.zhihu.com/p/68555964
Model-Agnostic Meta-Learning (MAML)模型介绍及算法详解
https://zhuanlan.zhihu.com/p/57864886
Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
李老师无监督学习讲座PPT
链接: https://pan.baidu.com/s/1saMSy4a0KSdK3MFLgQHSow
提取码: j5m4
#6. 遗传算法与神经网络
6.1 遗传演化神经网络
让计算机模仿遗传,赋予程序优化的力量。
-
遗传算法原理:遗传算法的整体搜索策略和优化搜索方法在计算时不依赖于梯度信息或其它辅助知识,只需要影响搜索方向的目标函数(Target Function)和相应的适应度函数(Fitness Function),所以遗传算法提供了一种求解复杂系统问题的通用框架,它不依赖于问题的具体领域,对问题的种类有很强的稳定性,所以广泛应用于许多科学。通俗易懂得来讲就是遗传算法能够解决很多问题,深度学习只是一个方向,大家只要有想法,随时随地都能将遗传用在别的问题上,比如路径规划、旅行商(TSP)问题和车间设施布局优化问题。
-
遗传算法整体流程
因为遗传算法是个通用框架,因此我们需要根据具体的问题来应用遗传算法。不过,既然它是框架,那它就会有通用的几部分供我们选择,因此笔者在此给大家先讲下整体的流程。整体框架可分为三部分:交叉、变异与适应度。
伪代码如下:
# 1.初始化种群 while condition: # 2.种群按照随机概率选取一个个体 if random.ramdom < 交叉率: 种群按照随机概率选取一个个体 交叉操作 if random.random < 变异率: 变异操作 计算(两者)适应度 else: # 直接变异 if random.random < 变异率: 变异操作 计算适应度 # 3.新生成的个体形成新的种群 condition: 迭代次数所以,整个流程可以理解为有一个种群,他们不断地生小孩(交叉与变异),适应环境(评价函数)的小孩和大人会被保留,不适应的环境的大人和小孩会被杀掉,通过不断地迭代,最终得到的种群是最适应环境的。另外,值得一提的是,上面所说的交叉、变异与适应度都是根据具体问题去定义的,所以才说遗传算法是个通用框架,能够解决很多问题
-
遗传算法遇上神经网络
随着深度的增加,深度神经网络持续表现出更好的性能,这是一个令人鼓舞的趋势,这意味着网络架构和超参数的可能排列发生了爆炸式增长,对此几乎没有直观的指导。为了解决这种日益增加的复杂性,Emmanuel等人[8]提出了演化神经网络(EDEN),这是一种计算效率高的神经进化算法,可与任何深层神经网络平台(例如TensorFlow)接口。他们展示了EDEN从嵌入,一维和二维卷积,最大池化和完全连接的层及其超参数发展而来的简单但成功的体系结构。
EDEN对七个图像和情感分类数据集的评估表明,它可以可靠地找到良好的网络-在三种情况下,即使在单个GPU上,也可以在6-24小时内达到最新的结果。EDEN的研究为将神经进化应用于创建一维卷积网络以进行情感分析(包括优化嵌入层)提供了首次尝试。
-
演化神经网络实验
因为演化神经网络EDEN的作者并没有开源论文的代码。为此,笔者通过疟疾细胞数据集[3]来实现一个演化神经网络模型来达到疟疾细胞分类(感染与未感染)的效果。伪代码如下:
https://lhncbc.nlm.nih.gov/publication/pub9932
-
超参数设置
物理计算环境:1080Ti GPU
卷积核数目范围:[10, 100]
卷积核大小范围:[1, 6]
网络层数范围:[2, 10]
max_pooling层大小范围:[1, 6]
全连接层神经元数目范围:[32,256]
dropout范围:(0, 1]
卷积层的激励函数选择范围:[linear, leaky relu, prelu, relu]
中间层全连接层的激励函数选择范围:[linear, sigmoid, softmax, relu]
最后一层全连接层的激励函数选择范围:[sigmoid, softmax]
-
整体流程
具体代码见链接: https://github.com/ChileWang0228/Deep-Learning-With-Python/blob/master/chapter6/6_1_4_EDEN.ipynb
-
6.2 遗传拓扑神经网络
Kenneth O. Stanley等人[9]提出的遗传拓扑神经网络(NEAT算法)同样也是结合了神经网络和遗传算法产生的一种全新模型。它与6.1节介绍的遗传演化神经网络不同的地方在于加入了交叉操作。
*6.2.1 遗传拓扑神经网络原理*
正如之前的6.1节所说,遗传算法是个通用框架,因此我们需要根据具体的问题来定义遗传算法。不过,既然它是框架,那它就会有通用的几部分供我们选择,因此博主在此给大家先讲下整体的流程。整体框架可分为三部分:交叉、变异与适应度。不过虽然整体的流程是一致的,但是因为问题不同,我们定义的基因也有所不同,那交叉与变异也会随之变化。
这篇论文将神经元及其连接定义成基因组,而遗传演化神经网络论文是将网络层及其学习率定义成基因组,大家可以对比着学习两者的异同,这样也能更好地感受为什么说遗传算法是解决一般性问题的通用框架,就是因为我们可以根据问题去定义基因组。
6.2.2 算法核心
-
超参数设置
个体基因:(结点链接与结点类型)
种群规模:150
物种划分:基于权值相似度划分物种
-
伪代码
while condition:
2. if random.random < 交叉率:
3. 选择操作(适应度越高,越容易被选中)
4. 物种内交叉
5. if random.random < 变异率:
6. 变异操作
7. 评估适应度
8. else: # 直接变异
9. if random.random < 变异率:
10. 变异操作
11. 评估适应度
12. # 淘汰操作
13. 每个物种保留一定数量的个体
14. if random.random < 灭绝率:
15. 灭绝最差的物种
16. 种群间的物种交叉生成亚种, 弥补新的物种
17.
18. conditon:迭代次数 or fittness达到设定的阈值
19. 评估适应度:fitness = 1/(训练集的误差)^2
20. 这里的适应度函数是自定义的,大家可以根据自己的想法去定义。
- 交叉操作
论文通过一个链表定义基因的节点连接,选择两个个体进行交叉的时候,按照链表的顺序,逐一操作,最后生成新的子代。如图 6.2所示
- NEAT实验
具体代码见链接: https://github.com/jingluo1208/Deep-Learning-With-Python
论文作者开源了NEAT的代码,所以我们可以通过官网的例子来巩固刚刚所学。官网的例子为实现一个XOR异或操作的网络。伪代码如下:
"""
异或:输入相异,输出1, 输入相同,输出0
"""
xor_inputs = [(0.0, 0.0), (0.0, 1.0), (1.0, 0.0), (1.0, 1.0)]
xor_outputs = [(0.0,), (1.0,), (1.0,), (0.0,)]
-
可视化操作
而且论文的作者也在代码中加入了可视化操作,为了能使用其可视化功能,我们需在命令行输入以下命令。
windows 用户: cmd命令行输入以下命令 conda install -c conda-forge graphviz conda install -c conda-forge python-graphviz linux 用户: 命令行输入以下命令 sudo apt-get install graphviz -
NEAT配置文件
因为论文作者对整个算法进行了很好得包装,所以我们只需要修改配置文件的相应参数,就可以运行Neat算法了,下面给大家介绍下Neat算法的配置文件,官网有对配置文件更详细的解释,这里标注只是标注一些自己用到的参数。
#chapter6/6_2_3_Neat/config-feedforward
#实验的超参数设置#
[NEAT]
fitness_criterion = max
fitness_threshold = 3.9 # 适应度的阈值
pop_size = 150 # 种群规模
reset_on_extinction = False
[DefaultGenome]
# node activation options # 结点的激励函数
activation_default = sigmoid
activation_mutate_rate = 0.0
activation_options = sigmoid
# node aggregation options # 结点的聚合选择 (一般默认)
aggregation_default = sum
aggregation_mutate_rate = 0.0
aggregation_options = sum
# node bias options # 结点的偏置选择
bias_init_mean = 0.0
bias_init_stdev = 1.0
bias_max_value = 30.0
bias_min_value = -30.0
bias_mutate_power = 0.5
bias_mutate_rate = 0.7
bias_replace_rate = 0.1
# genome compatibility options # 基因组兼容性选项
compatibility_disjoint_coefficient = 1.0
compatibility_weight_coefficient = 0.5
# connection add/remove rates # 连接增加/删除的概率
conn_add_prob = 0.5
conn_delete_prob = 0.5
# connection enable options
enabled_default = True
enabled_mutate_rate = 0.01
feed_forward = True # 是否加入RNN神经元
initial_connection = full
# node add/remove rates # 结点的添加和删除概率
node_add_prob = 0.2
node_delete_prob = 0.2
# network parameters # 输入层、输出层、隐藏层的神经元个数
num_hidden = 2
num_inputs = 2
num_outputs = 1
# node response options # 节点相应选项
response_init_mean = 1.0
response_init_stdev = 0.0
response_max_value = 30.0
response_min_value = -30.0
response_mutate_power = 0.0
response_mutate_rate = 0.0
response_replace_rate = 0.0
# connection weight options # 连接权重选项
weight_init_mean = 0.0
weight_init_stdev = 1.0
weight_max_value = 30
weight_min_value = -30
weight_mutate_power = 0.5
weight_mutate_rate = 0.8
weight_replace_rate = 0.1
[DefaultSpeciesSet]
# genomic distance小于此距离被认为是同一物种
compatibility_threshold = 3.0
[DefaultStagnation]
species_fitness_func = max
max_stagnation = 20
species_elitism = 2
[DefaultReproduction]
elitism = 2 # 保留最优的个体遗传到下一代的个数
survival_threshold = 0.2 # 每一代每个物种的存活率
- 主函数
# /chapter6/6_2_3_Neat/xor.ipynb
from __future__ import print_function
import os
import neat
import visualize
# XOR异或的输入输出数据
xor_inputs = [(0.0, 0.0), (0.0, 1.0), (1.0, 0.0), (1.0, 1.0)]
xor_outputs = [ (0.0,), (1.0,), (1.0,), (0.0,)]
def eval_genomes(genomes, config):
# 评估函数
for genome_id, genome in genomes:
genome.fitness = 4.0
net = neat.nn.FeedForwardNetwork.create(genome, config)
for xi, xo in zip(xor_inputs, xor_outputs):
output = net.activate(xi)
genome.fitness -= (output[0] - xo[0]) ** 2
def run(config_file):
# 读取配置配置文件
config = neat.Config(neat.DefaultGenome, neat.DefaultReproduction,
neat.DefaultSpeciesSet, neat.DefaultStagnation,
config_file)
# 创建种群
p = neat.Population(config)
# 打印训练过程
p.add_reporter(neat.StdOutReporter(True))
stats = neat.StatisticsReporter()
p.add_reporter(stats)
p.add_reporter(neat.Checkpointer(5))
# 迭代300次
winner = p.run(eval_genomes, 300)
# 显示最佳网络
print('\nBest genome:\n{!s}'.format(winner))
print('\nOutput:')
winner_net = neat.nn.FeedForwardNetwork.create(winner, config)
for xi, xo in zip(xor_inputs, xor_outputs):
output = winner_net.activate(xi)
print("input {!r}, expected output {!r}, got {!r}".format(xi, xo, output))
node_names = {
-1:'A', -2: 'B', 0:'A XOR B'}
visualize.draw_net(config, winner, True, node_names=node_names)
visualize.plot_stats(stats, ylog=False, view=True)
visualize.plot_species(stats, view=True)
p = neat.Checkpointer.restore_checkpoint('neat-checkpoint-4')
p.run(eval_genomes, 10)
if __name__ == '__main__':
58. config_path = os.path.join('config-feedforward')
59. run(config_path)
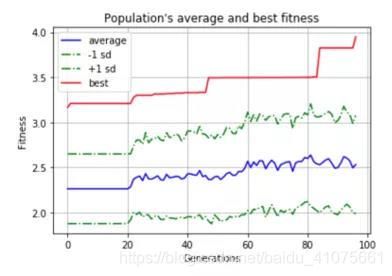
实验结果:生成的.svg后缀文件用google浏览器打开即可。实验结果显示的是遗传拓扑神经网络的结构图与其fitness趋势,如图 6.4与图 6.5所示。大家在掌握了整个流程之后,可以把官方代码下载下来,调一下配置文件,就可以运行了。当然,有些读者可能会想着自己定义一个新的交叉或者变异操作,这就需要对着Neat算法的源码修改相应的代码了。
图 6.4 网络结构图
图 6.5 fitness趋势图
7. 迁移学习与计算机视觉
在某些领域如生物信息,由于其数据获取和数据标注都需要进行大量的临床试验,因此很难构建大规模带有标注的高质量数据集,从而限制了它的发展。为此,有人提出了迁移学习,这放松了数据获取的假设:只要求训练数据必须独立且与测试数据相同分布(i.i.d.),这促使我们可以使用迁移学习来解决训练数据不足的问题。
迁移学习就像在讲诉一个站在巨人肩膀的故事。随着越来越多的深度学习应用场景的出现,人们不可避免会去想,如何利用已训练的模型去完成相类似的任务,毕竟重新训练一个优秀的模型需要耗费大量的时间和算力,而在前人的模型进行改进,进而举一反三无疑是最好的办法。笔者将在这章给大家介绍迁移学习与计算机视觉的故事。
7.1 计算机视觉
计算机视觉的任务是识别和理解图像或者视频中的内容。
如今,互联网上超过70%的数据是图像或者视频,全世界的摄像头数目已超过人口数,每天有数以亿计小时的视频数据生成。因此,我们需要自动化的计算机视觉技术才能处理如此大的数据量,这也是近年来计算机视觉能够蓬勃发展的原因。接下来,笔者将介绍计算机视觉的4个基础任务。
7.1.1 图像分类
给定一张输入图像,图像分类任务只要判断出该图像的类别即可。
7.1.2 目标检测
(object detection)。目标检测是将图像中出现的不同类别的目标识别出来,如图 7.1所示。
7.1.3 语义分割
(semantic segmentation):语义分割是目标检测更进阶的任务,目标检测只需要圈出每个目标的包围盒,语义分割则需要判断图像中哪些像素对应于哪些目标,也就是对图像中的每一个像素进行分类,如图 7.2所示。
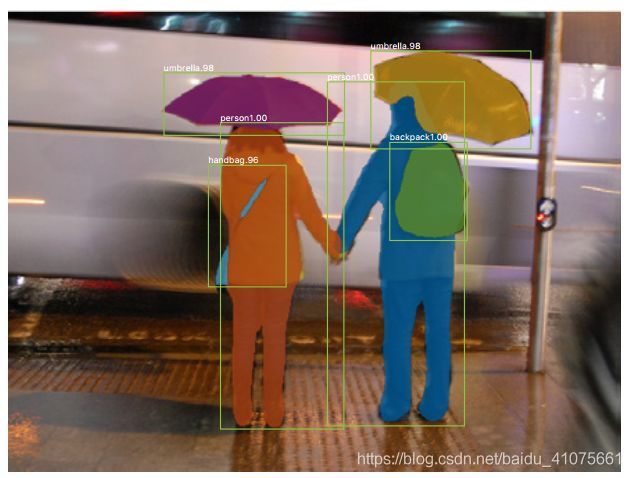
7.1.4 实例分割
(instance segmentation):实例分割则是目标检测与语义分割的综合任务。语义分割不区分属于相同类别的不同实例。如图X所示,当图像中有两个人时,语义分割会将所有人的像素预测为“person”这个类别。实例分割则需要区分出“person”这个类别下每一个人的实例,如图 7.3所示。
7.2 迁移学习与图像分类
迁移学习(Transfer Learning) 顾名思义就是将训练好的模型(预训练模型)参数迁移到新的模型来优化新模型训练。因为大部分的数据和任务都是存在相关性的,所以我们可以通过迁移学习将预训练模型的参数(也可理解为预训练模型学到的知识)通过某种方式迁移到新模型,进而加快并优化模型的学习效率。其中,实现迁移学习有以下三种方式:
- 直接迁移: 冻结预训练模型的全部卷积层,删除预训练模型的全连接层,添加并训练自己定制的全连接层。
- 提取特征向量: 抽取预训练模型的卷积层对所有数据的特征向量,将特征向量灌入自己自己定制的全连接网络。
- Fine-tune: 冻结预训练模型的部分卷积层,甚至不冻结任何网络层,训练非冻结层和自己定制的全连接层。
接下来笔者将通过Karen Simonyan等人[10]提出的VGG-16模型和Saining Xie等人[11]提出的ResNeXt来介绍计算机视觉是如何站在迁移学习的肩膀上发扬光大的。
7.2.1 VGG
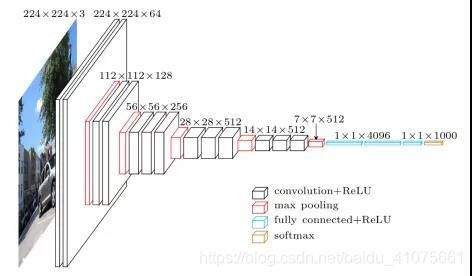
VGG是由牛津的Visual Geometry Group提出的预训练模型,所以VGG名字的由来就是取这三个单词的首字母。VGG16是采用的结构非常简洁,整个网络都使用了同样大小的卷积核尺寸(3×3)和max pooling层(2x2),VGG的结构有两种,分别是16层结构(13个卷积层与3个全连接层)与19层结构(16个卷积层与3个全连接层),如表 7.1和图 7.4所示。
图 7.4
至于为什么采用3×3的卷积核,原因也很简单:对于给定的感受野,使用堆叠的小卷积核是优于采用大的卷积核,因为多层非线性层的堆叠能够增加网络深度,从而保证模型能够学习更复杂的模式,而且因为小卷积核的参数更少,所以整个网络的计算代价比较小。
7.2.2 VGG16与图像分类
图像分类是计算机视觉任务中最基础也是最为简单的任务。在7.2.1节我们提到的3种实现迁移学习的手段,都可以用在图像分类任务,整体的思路就是拆掉VGG16的全连接层,定制自己的全连接层,以适应我们当前的任务。
举个例子,加入我们需要训练一个3分类模型,而VGG16可以识别1000类的物体。我们当然不需要识别这么多类别的模型,因为VGG16一半以上的参数都是来自全连接层,而拆掉全连接层对图像任务几乎没有影响。为此,我们可以拆掉VGG16的全连接层,而后再添加一个识别3分类的全连接层结构,这样就大大减少了我们模型的参数,而且我们的定制模型还可以借助VGG16卷积层学到的知识更好地完成图像分类任务。
7.3 迁移学习与目标检测
(faster RCNN)
目标检测的任务是将图像中不同种类的目标圈出来,而VGG16在目标检测任务中则是扮演充当图像特征抽取器的角色。当前,目标检测有很多种算法如YOLO、RCNN、fast RCNN和faster RCNN等。我们只需要学习最新最强的目标检测算法即可,为此,笔者将介绍由Shaoqing Ren等人[12]当前最优的目标检测算法faster RCNN。整个faster R-CNN分为4大部分:共享卷积网络、候选检测框生成网络RPN(Region Proposal Networks)、Roi(Region of Interest)Pooling和Classifier,如图 7.5所示。
7.3.1 共享卷积网络
G16模型提取图像特征给RPN与Roi网络
7.3.2 RPN网络
对图像特征图生成候选框,如图 7.6所示。
-
锚点anchor
对每一个点使用3种尺寸与3种缩放率来生成候选框anchor(即对特征图中的每一个点初始化九个候选框),因此每一张特征图总共有W × H × k个anchor,又因为VGG输出的特征图有512张,因此总的锚点数为W × H × k × 512个anchor。其中,W为宽度,H为高度,k为9
-
cls layer和reg layer
将512张特征图上的anchor转化为W × H × 512 × 2k scores和W × H × 512 × 4k coordinates。其中,2k scores被cls layer用以分类anchor是否属于positive(positive代表候选框,negative代表非候选框),最后我们用2×k的矩阵装载k个anchor是否属于候选框的概率。输出的矩阵大小为W × H × 512 × 2k。而4k coordinates则被reg layer用以编码每个anchor的4个坐标值,如公式(7.1)和(7.2)所示。
-
训练RNP网络
-
优化器:stochastic gradient descent (SGD)。
-
训练数据:每张图片随机选取128个positive anchors和128个negative anchors作为训练样本,若positive anchors数目不够,则用negative anchors来填充。这样做的好处是避免了负样本过多的情况与训练的anchors数目过多的情况,从而保证训练效果。
-
损失函数:如公式(7.3)所示。
-
RPN网络的输出:W × H × 512 × 2k的分类特征矩阵和W × H × 512 × 4k的坐标回归矩阵。
-
proposals:结合分类矩阵和坐标矩阵计算出更加精确的候选区域,送入Roi层。
总的来说,cls layer的用途是分类候选框, reg layer的用途是让预测的坐标值在训练过程中不断接近真实坐标值。
-
Roi(Region of Interest)Pooling
RPN在特征图中会产生尺寸不一致的Proposal区域,而在Faster RCNN中,之后的分类网络输入尺寸固定为7 × 7,所以对于任意大小的输入,都用7 × 7的网格覆盖原区域的每一个网格,而后在新形成的区域上,取原先格子覆盖区域内的最大值(max pooling)。这样的操作使得任意大小的Proposal都能被pooling成了7*7的尺寸,如图 7.7所示
- 锚点anchor
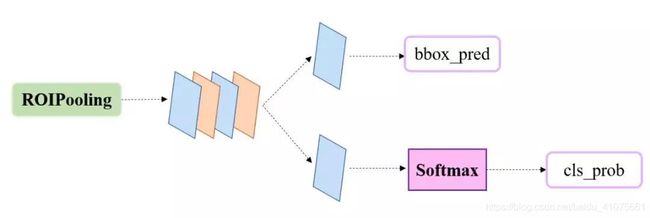
classifier部分利用已经获得的proposal feature maps,通过全连接层与Softmax计算每个proposal具体属于那个类别(如人,车,电视等),输出cls_prob概率向量;同时再次利用bounding box regression获得每个proposal的位置偏移量bbox_pred,用于回归更加精确的目标检测框。classifier网络结构如图 7.8所示。
7.4 迁移学习与语义分割
(Seg Net)
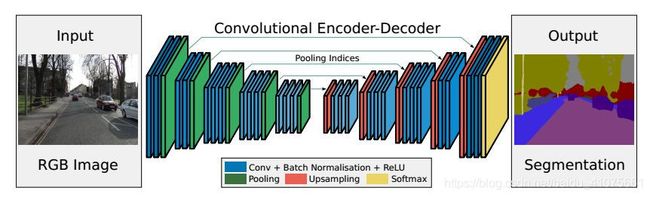
语义分割的任务是将图像每一个像素进行分类,而VGG16在语义分割任务中则是扮演充当图像编码器的角色。Vijay Badrinarayanan等人[13]提出了SegNet模型便很好地完成该项任务,模型结构如图 7.9所示。类似于我们在第四章提及的卷积自编码器,SegNet也是采用Encoder-Decoder模式。编码器由VGG16的前13层组成(即去掉了全连接层),每个卷积层后面跟着Batch Normalization和Relu激励函数,而译码器则是和编码器每一层都相对应,最后下接一个Softmax层来进行分类,进而输出每一个像素的标签。(图-7.9)
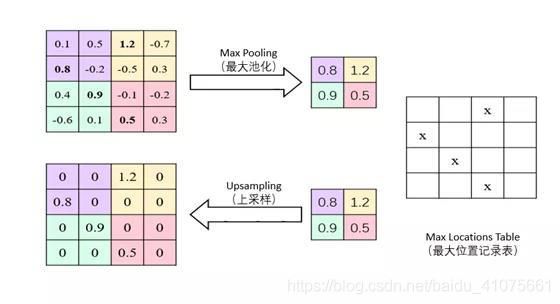
这个模型最大的亮点是采用了Pooling Indices,通过记录每一次Max Pooling的最大值和位置,从而建立索引查询。在upsampling过程中,我们直接利用记录的索引恢复像素,从而达到定向恢复相应值的效果,进而达到分类更加精细的目标。而且这样做的另外一个好处是耗费少量存储空间,加快了训练速度。因为我们只是将对应记录的Max pooling的最大值放回原来的位置,并不需要通过Upsampling来训练学习。Max Pooling与其相对应的UpSampling运算过程如图 7.10所示。
7.5 迁移学习与实例分割
(ResNeXt)
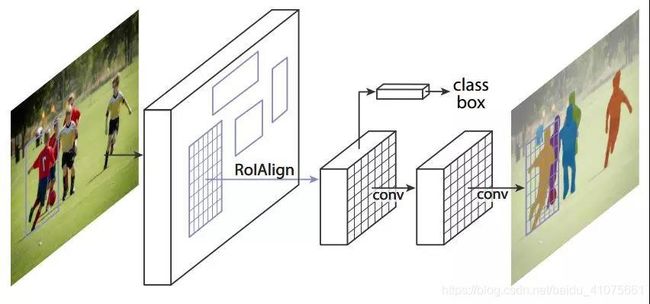
实例分割的任务是将先用目标检测方法将图像中的不同实例框出,再用语义分割方法在不同包围盒内进行逐像素分类,本质上就是目标检测与语义分割的综合任务。Kaiming He等人[14]提出的Mask R-CNN模型则能完成实例分割任务,模型结构如图 7.11所示。它整体的网络还是采用faster RCNN的框架结构,只不过是在faster RCNN的基础上增加了语义分割方法,也就是多加了一个全连接卷积网络分支,从而将原本的双任务(分类,回归)转换成了三任务(分类,回归,分割)。此时整体网络的loss为公式(7.5)所示。
与此同时,Mask R-CNN也对网络结构做了相应的改进:
- 使用了更好的特征抽取器如ResNeXt-101+FPN作为基础网络。其中,FPN是由Lin等人[***]提出的一种有效的网络,全称为特征金字塔中间网络(Feature Pyramid Network)。FPN使用具有横向连接的自上而下的体系结构,可以根据单比例输入构建网络内要素金字塔。具有FPN的基础网络可以根据特征金字塔的规模从不同级别的功能金字塔中提取RoI特征。使用ResNet-FPN作为基础网络进行特征提取,可以在准确性和速度上获得出色的收益。
- RoIAlign:虽然微小偏移对目标检测任务影响不大,但却对像素级别分类的实例分割准确率却有致命影响。为了解决这个问题,作者提出RoiAlign层来解决Roil Pool对特征图量化(即Max Pooling)导致得到的mask与实践物体产生微小偏移的问题,具体的操作就是对特征图上每一个点插多个值以消除量化影响。
如图 7.12所示,虚线网格表示一个特征图,实线表示RoI(在此示例中为2×2格),RoIAlign通过双线性插值在一个点中插入多个值,再进行量化,相当于没有执行量化操作或者降低了量化带来的影响。(图-7.12)

7.6 迁移学习与计算机视觉实践
本节开始,我们将使用VGG16模型做一些小实验,进而巩固我们对迁移学习与计算机视觉理论知识的理解。与第四章一样,我们同样是基于fashion MNIST数据的图像分类去做实验。
在2017年8月份,德国研究机构Zalando Research在GitHub上推出了一个全新的数据集,其中训练集包含60000个样例,测试集包含10000个样例,分为10类,每一类的样本训练样本数量和测试样本数量相同。样本都来自日常穿着的衣裤鞋包,每个都是28×28的灰度图像,其中总共有10类标签,每张图像都有各自的标签。值得注意的是,因为VGG16只能识别尺寸大于48×48的彩色图片,而我们的数据集是28×28的灰色图片,因此我们在将数据集灌入迁移学习模型前,要对图片数据集进行适当地转换,也就是比第四章中传统CNN神经网络的图像预处理多了一步:将图片转换成48×48大小的彩色图片。
7.6.1 实验环境
- Anaconda Python 3.7与Jupyter Notebook
- Keras
- fashion MNIST数据数据集
7.6.2 实验流程
- 加载图像数据
- 图像数据预处理
- 训练模型
- 保存模型与模型可视化
- 训练过程可视化
# chapter7/7_3_Transfer_learning_cnn_image.ipynb
from tensorflow.python.keras.utils import get_file
import gzip
import numpy as np
import keras
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
import os
from keras import applications
import cv2
import functools
from keras.models import load_model
# os.environ["CUDA_VISIBLE_DEVICES"] = "1" # 使用第2个GPU
# 1. 读取数据与数据预处理
# 数据集与代码放在同一个文件夹即可
def load_data():
paths = [
'train-labels-idx1-ubyte.gz', 'train-images-idx3-ubyte.gz',
't10k-labels-idx1-ubyte.gz', 't10k-images-idx3-ubyte.gz'
]
with gzip.open(paths[0], 'rb') as lbpath:
y_train = np.frombuffer(lbpath.read(), np.uint8, offset=8)
with gzip.open(paths[1], 'rb') as imgpath:
x_train = np.frombuffer(
imgpath.read(), np.uint8, offset=16).reshape(len(y_train), 28, 28, 1)
with gzip.open(paths[2], 'rb') as lbpath:
y_test = np.frombuffer(lbpath.read(), np.uint8, offset=8)
with gzip.open(paths[3], 'rb') as imgpath:
x_test = np.frombuffer(
imgpath.read(), np.uint8, offset=16).reshape(len(y_test), 28, 28, 1)
return (x_train, y_train), (x_test, y_test)
# 读取数据集
(x_train, y_train), (x_test, y_test) = load_data()
batch_size = 32
num_classes = 10
epochs = 5
data_augmentation = True # 图像增强
num_predictions = 20
save_dir = os.path.join(os.getcwd(), 'saved_models_transfer_learning')
model_name = 'keras_fashion_transfer_learning_trained_model.h5'
# 将类别弄成独热编码
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
# 由于mist的输入数据维度是(num, 28, 28),因为vgg16 需要三维图像,所以扩充mnist的最后一维
X_train = [cv2.cvtColor(cv2.resize(i, (48, 48)), cv2.COLOR_GRAY2RGB) for i in x_train]
X_test = [cv2.cvtColor(cv2.resize(i, (48, 48)), cv2.COLOR_GRAY2RGB) for i in x_test]
x_train = np.asarray(X_train)
x_test = np.asarray(X_test)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255 # 归一化
x_test /= 255 # 归一化
# 2. 迁移学习建模
# 使用VGG16模型
# 将VGG16的卷积层作为基底网络
base_model = applications.VGG16(include_top=False, weights='imagenet', input_shape=x_train.shape[1:]) # 第一层需要指出图像的大小
print(x_train.shape[1:])
model = Sequential() # 自定义网络
print(base_model.output)
model.add(Flatten(input_shape=base_model.output_shape[1:]))
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
# VGG16模型与自己构建的模型合并
model = Model(inputs=base_model.input, outputs=model(base_model.output))
# 保持VGG16的前15层权值不变,即在训练过程中不训练
for layer in model.layers[:15]:
layer.trainable = False
# 初始化优化器
opt = keras.optimizers.rmsprop(lr=0.0001, decay=1e-6)
# Let's train the model using RMSprop
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
# 3. 训练
if not data_augmentation: # 是否选择数据增强
print('Not using data augmentation.')
history = model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
shuffle=True)
else:
print('Using real-time data augmentation.')
datagen = ImageDataGenerator(
featurewise_center=False,
samplewise_center=False,
featurewise_std_normalization=False,
samplewise_std_normalization=False,
zca_whitening=False,
zca_epsilon=1e-06,
rotation_range=0,
width_shift_range=0.1,
height_shift_range=0.1,
shear_range=0.,
zoom_range=0.,
channel_shift_range=0.,
fill_mode='nearest',
cval=0.,
horizontal_flip=True,
vertical_flip=False,
rescale=None,
preprocessing_function=None,
data_format=None,
validation_split=0.0)
datagen.fit(x_train)
print(x_train.shape[0]//batch_size) # 取整
print(x_train.shape[0]/batch_size) # 保留小数
# 按batch_size大小从x,y生成增强数据
history = model.fit_generator(datagen.flow(x_train, y_train,
batch_size=batch_size),
epochs=epochs,
steps_per_epoch=x_train.shape[0]//batch_size,
validation_data=(x_test, y_test),
# 在使用基于进程的线程时,最多需要启动的进程数量。
workers=10
)
# 4. 保存模型与模型可视化
model.summary() # 模型可视化
# 保存模型
if not os.path.isdir(save_dir):
os.makedirs(save_dir)
model_path = os.path.join(save_dir, model_name)
model.save(model_path)
print('Saved trained model at %s ' % model_path)
# 5. 训练过程可视化
import matplotlib.pyplot as plt
# 绘制训练 & 验证的准确率值
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Valid'], loc='upper left')
plt.savefig('tradition_cnn_valid_acc.png')
plt.show()
# 绘制训练 & 验证的损失值
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Valid'], loc='upper left')
plt.savefig('tradition_cnn_valid_loss.png')
plt.show()
8. 迁移学习与自然语言处理
迁移学习一路前行,走进了自然语言处理的片场。迁移学习在自然语言处理(NLP)领域同样也是一种强大的技术。由这种技术训练出来的模型,我们称之为预训练模型。预训练模型首先要针对数据丰富的任务进行预训练,然后再针对下游任务进行微调,以达到下游任务的最佳效果。迁移学习的有效性引起了理论和实践的多样性,人们通过迁移学习与自然语言处理两者相结合,高效地完成了各种NLP的实际任务。
8.1 BERT的原理与应用
自然语言处理预训练模型
使语言建模和其他学习问题变得困难的一个基本问题是维数的诅咒。在人们想要对许多离散的随机变量(例如句子中的单词或数据挖掘任务中的离散属性)之间的联合分布建模时,这一点尤其明显。
举个例子,假如我们有10000个单词的词汇表,我们要对它们进行离散表示,这样用one-hot 编码整个词汇表就需要10000*10000的矩阵,而one-hot编码矩阵存在很多“0”值,显然浪费了绝大部分的内存空间。为了解决维度诅咒带来的问题,人们开始使用低维度的向量空间来表示单词,从而减少运算资源的损耗,这也是预训练模型思想的开端。
8.1.1 Word2Vec模型
在4.7.2节的实验中,我们提及了Skip-gram模型,它就是Yoshua Bengio等人[1]提出的经典Word2Vec模型之一。Word2Vec模型对NLP任务的效果有显著的提升,并且能够利用更长的上下文。对于Word2Vec具体的原理与应用,笔者在4.7.2节已经进行了详细的讲解,而且本章的主角并不是它,所以笔者就不进行赘述了。
8.1.2 BERT
在2018年,什么震惊了NLP学术界?毫无疑问是Jacob Devlin等人[2]提出的预训练模型BERT(Bidirectional Encoder Representations from Transformers)。BERT被设计为通过在所有层的双向上下文上共同进行条件化来预训练未标记文本的深层双向表示。我们可以在仅一个附加输出层的情况下对经过预训练的BERT模型进行微调,以创建适用于各种任务(例如问题解答和语言推断)的最新模型,进而减少了对NLP任务精心设计特定体系结构的需求。BERT是第一个基于微调的表示模型,可在一系列句子级和字符级任务上实现最先进的性能,优于许多特定于任务的体系结构。
通俗易懂来讲就是我们只需要把BERT当成一个深层次的Word2Vec预训练模型,对于一些特定的任务,我们只需要在BERT之后下接一些网络结构就可以出色地完成这些任务。
另外,2018年底提出的BERT推动了11项NLP任务的发展。BERT的结构是来自Transformers模型的Encoder,Transformers如图 8.1所示。我们从图X中可以看到Transformer的内部结构都是由Ashish Vaswani 等人[3]提出的Self-Attention Layer和Layer Normalization的堆叠而产生。Transformers(左边为Encoder,右边为Decoder)(图-8.1 )
1. Self-Attention Layer原理
-
Self-Attention Layer的出现原因: 为了解决RNN、LSTM等常用于处理序列化数据的网络结构无法在GPU中并行加速计算的问题。
-
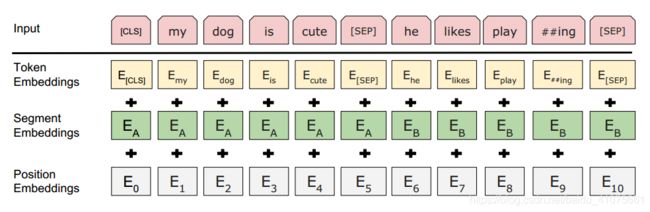
Self-Attention Layer的输入: 如图8.2所示:将输入的Input转化成token embedding + segment embedding +position embedding。因为有时候训练样本是由两句话组成,因此“[CLS]”是用来分类输入的两句话是否有上下文关系,而“[SEP]”则是用以分开两句话的标志符。其中,因为这里的Input是英文单词,所以在灌入模型之前,需要用BERT源码的Tokenization工具对每一个单词进行分词,分词后的形式如图 8.2中Input的“Playing”转换成“Play”+“# #ing”,因为英文词汇表是通过词根与词缀的组合来新增单词语义的,所以我们选择用分词方法可以减少整体的词汇表长度。如果是中文字符的话,输入就不需要分词,整段话的每一个字用“空格”隔开即可。值得注意的是,模型是无法处理文本字符的,所以不管是英文还是中文,我们都需要通过预训练模型BERT自带的字典vocab.txt将每一个字或者单词转换成字典索引(即id)输入。
-
segment embedding的目的:有些任务是两句话一起放入输入X,而segment便是用来区分这两句话的。在Input那里就是用“[SEP]”作为标志符号。而“[CLS]”用来分类输入的两句话是否有上下文关系。
-
position embedding的目的:因为我们的网络结构没有RNN 或者LSTM,因此我们无法得到序列的位置信息,所以需要构建一个position embedding。构建position embedding有两种方法:BERT是初始化一个position embedding,然后通过训练将其学出来;而Transformer是通过制定规则来构建一个position embedding:使用正弦函数,位置维度对应曲线,而且方便序列之间的选对位置,使用正弦会比余弦好的原因是可以在训练过程中,将原本序列外拓成比原来序列还要长的序列,如公式(8.1)~(8.2)所示。
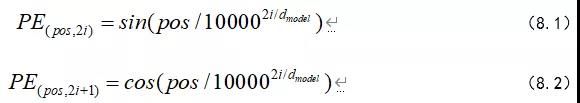
图 8.2 Self-Attention的输入
-
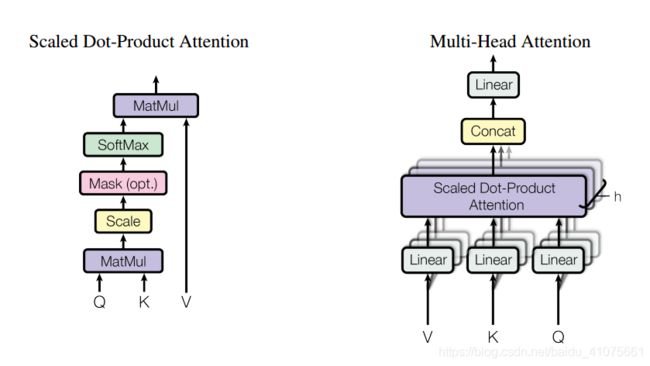
首先,将 Q与K 矩阵乘积并scale(为了防止结果过大,除以他们维度的均方根),其次,将其灌入Softmax函数得到概率分布,最后再与V 矩阵相乘,得到self-attention的输出,如公式(8.3)所示。其中,(Q,K,V) 均来自同一输入X ,他们是 X分别乘上 WQ,WK,WV初始化权值矩阵所得,而后这三个权值矩阵会在训练的过程中确定下来,如图 8.3所示。

图 8.3初始化(Q,K,V)
通过Linear线性投影来初始化不同的(Q,K,V) ,将多个单头的结果融合会比单头Self-Attention的效果好。我们可以将初始化不同的(Q,K,V) 理解为单头从不同的方向去观察文本,这样使Self-Attention更加具有“大局观”。整体的运算逻辑就是Multi-Head Self-Attention将多个不同单头的Self-Attention输出Concat成一条,然后再经过一个全连接层降维输出,如图 8.4所示。
图 8.4 Multi-Head Self-Attention(左边为单头Self-Attention运算逻辑,右边为多头Self-Attention运算逻辑)
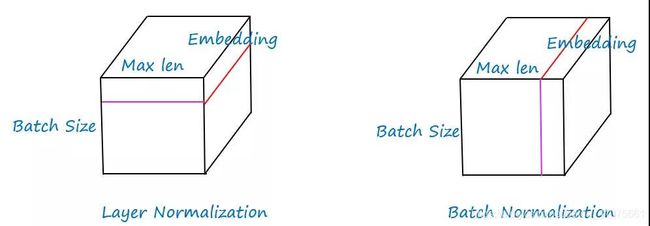
2. Layer Normalization
Self-Attention的输出会经过Layer Normalization,为什么选择Layer Normalization而不是Batch Normalization?此时,我们应该先对我们的数据形状有个直观的认识,当一个batch的数据输入模型的时候,形状是长方体如图 8.5所示,大小为(batch_size, max_len, embedding),其中batch_size为batch的批数,max_len为每一批数据的序列最大长度,embedding则为每一个单词或者字的embedding维度大小。而Batch Normalization是对每个Batch的每一列做normalization,相当于是对batch里相同位置的字或者单词embedding做归一化,Layer Normalization是Batch的每一行做normalization,相当于是对每句话的embedding做归一化。显然,LN更加符合我们处理文本的直觉。
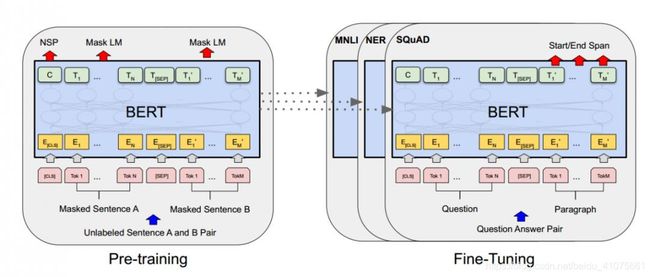
3. BERT预训练
如图 8.6所示。
-
预训练过程是生成BERT模型的过程一般来说,
个人用不着自己训练一个BERT预训练模型,都是直接调用模型的权重,进行fine-tune以适应当前特定任务,但我们可以了解一下BERT是怎么训练出来的。
-
输入X
就是Self-Attention Layer的输入,利用字典将每一个字或者单词用数字表示,并转换成token embedding + segment embedding + position embedding。序列的长度一般有512 或者 1024,不足用“[PAD]”补充。句子开头第一个位置用“[CLS]”表示,如果是输入两句话,则用“[SEP]”隔开。
-
MaskLM策略对于输入X,15%的字或者英文单词采用随机掩盖策略。对于这15%的字或者英文单词,80%的概率用“[mask]”替换序列中的某个字或者英文单词,10%的概率替换序列中的某个字或者英文单词,10%的概率不做任何变换。
-
训练语料总量
330亿语料
-
预训练
两种训练同时进行:
-
预测被掩盖的字或者英文单词(MaskLM)。
-
预测两句话之间是否有顺序关系(Next Sentence Prediction)。
这里需要补充说明的是NLP的预训练模型与计算机视觉的预训练模型有些许不同,NLP的预训练方式采用的是无监督学习,即我们不需要人工打标签,而计算机视觉需要则需要对图像进行人工分类。因为NLP的预训练正如笔者所说,只是预测被掩盖的单词或者字,以及判断是两段话是否有顺序关系,这些只需要写个小程序就可以轻松得到相应的标签,无需人工进行大量的标记。
-
-
预训练BERT模型权重
最后经过大量语料的无监督学习,我们得到了BERT预训练模型,BERT自带字典vocab.txt的每一个字或者单词都被768维度的embedding(即权重)所表示。当我们需要完成特定任务时,若对它们的embedding进行微调(即fine-tune),还能更好的适应任务。
4. BERT的 fine-tune过程
如图 8.6所示。
可以选择是否fine-tune(微调),如果不选择fine-tune,那就是简单地使用BERT的权重,把它完全当成文本特征提取器使用;若使用fine-tune,则相当于在训练过程中微调BERT的权重,以适应我们当前的任务。
文章提及到如果选择下面这几个参数进行fine-tune调参,任务的完成度会比较好。
- Batch Size:16 or 32;
- Learning Rate: 5e-5, 3e-5, 2e-5;
- Epochs:2, 3, 4;
8.1.3 RoBERTa
语言模型的预训练带来了可观的性能提升,但是不同方法之间的仔细比较却是一项艰巨的任务。Yinhan Liu等人[1]认为超参数的选择对最终结果有重大影响,为此他们提出了BERT预训练的重复研究,其中包括对超参数调整和训练集大小的影响的仔细评估。最终,他们发现了BERT的训练不足,并提出了一种改进的模型来训练BERT模型(称为RoBERTa(A Robustly Optimized BERT Pre-training Approach)),该模型可以媲美或超过所有Post-BERT的性能。而且他们对超参数与训练集的修改也很简单,它们包括:
- 训练模型时间更长,Batch Size更大,数据更多。
- 删除下一句预测目标(Next Sentence Prediction)。
- 对较长序列的训练。
- 动态掩盖应用于训练数据的掩盖模式。在BERT源码中,随机掩盖和替换在开始时只执行一次,并在训练期间保存,我们可以将其看成静态掩盖。BERT的预训练依赖于随机掩盖和预测被掩盖字或者单词。为了避免在每个epoch中对每个训练实例使用相同的掩盖,论文作者将训练数据重复10次,以便在40个epoch中以10种不同的方式对每个序列进行掩码。因此,每个训练序列在训练过程中都会看到相同的掩盖四次。他们将静态掩盖与动态掩盖进行了比较,实验证明了动态掩盖的有效性。
- 他们还收集了一个大型新数据集(CC-NEWS),其大小与其他私有数据集相当,以更好地控制训练集大小效果。
- 使用Sennrich[2]等人提出的Byte-Pair Encoding (BPE)字符编码,它是字符级和单词级表示之间的混合体,可以处理自然语言语料库中常见的大词汇,避免训练数据出现更多的“[UNK]”标志符号,从而影响预训练模型的性能。其中,“[UNK]”标记符表示当在BERT自带字典vocab.txt找不到某个字或者英文单词时,则用“[UNK]”表示。
8.1.4 ERNIE
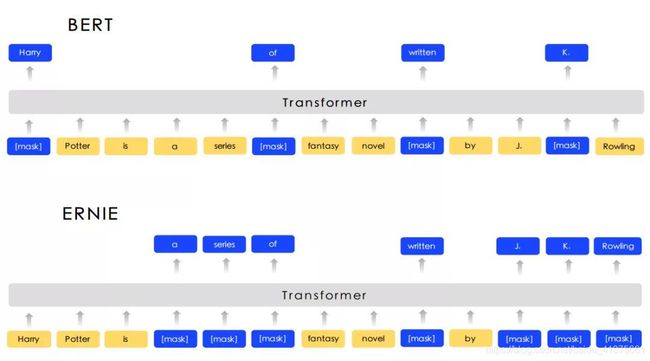
受到BERT掩盖策略的启发,Yu Sun等人[3]提出了一种新的语言表示模型ERNIE(Enhanced Representation through kNowledge IntEgration)。
ERNIE旨在学习通过知识掩盖策略增强模型性能,其中包括实体级掩盖和短语级掩盖,两者对比如图 8.7所示。实体级策略可掩盖通常由多个单词组成的实体。短语级策略掩盖了由几个单词组合成一个概念单元组成的整个短语。实验结果表明,ERNIE优于其他基准方法,在五种中文自然语言处理上获得了最新的最新结果任务包括自然语言推理,语义相似性,命名实体识别,情感分析和问题解答。他们还证明ERNIE在完形填空测试中具有更强大的知识推理能力。知识掩盖策略如图 8.8所示。
图 8.7 三种掩盖策略对比
图 8.8 知识掩盖策略
8.1.5 BERT_WWM
BERT已在各种NLP任务中取得了惊人的改进,因此基于BERT的改进模型接踵而至,带有全字掩码(Whole Word Masking)的BERT升级版本BERT_WWM便是其中之一,它减轻了预训练过程中掩码部分Word Piece字符的弊端。其中,Word Piece字符其实就是笔者在8.1.2节介绍的英文单词分词,在将英文单词灌入模型之前,我们需要将其转换成词根词缀形式,如“Playing”转换成“Play”+“# #ing”。如果我们使用原生BERT的随机掩盖,可能会掩盖“Play”或者“# #ing”或者同时掩盖两者,但如果我们使用全字掩盖,则一定是掩盖两者。
Yiming Cui等人[4]对中文文本也进行了全字掩码,这会掩盖整个词组,而不是掩盖中文字符。实验结果表明,整个中文词组被掩盖可以带来显着的收益。BERT_WWM的掩盖策略本质上和ERNIE是相同的,所以笔者在此就不进行过多的分析了。BERT_WWM掩盖策略如图 8.9所示。
8.1.6 NLP预训练模型对比
Word2Vec等模型已经比不上BERT与后续改进BERT的预训练模型了,除非我们对时间与空间复杂度要求非常苛刻,只能用小模型去完成某些特定任务,不然一般都是考虑用BERT之类的大模型来提升整体任务的准确率。
8.2 BERT四大下游任务
正如8.1.2节所说,BERT等预训练模型的提出,简化了我们对NLP任务精心设计特定体系结构的需求,我们只需在BERT等预训练模型之后下接一些网络结构,即可出色地完成特定任务。原因也非常简单,BERT等预训练模型通过大量语料的无监督学习,已经将语料中的知识迁移进了预训练模型的Eembedding中,为此我们只需在针对特定任务增加结构来进行微调,即可适应当前任务,这也是迁移学习的魔力所在。
BERT在概念上很简单,在经验上也很强大。它推动了11项自然语言处理任务的最新技术成果,而这11项NLP任务可分类为四大自然语言处理下游任务。为此,笔者将以BERT预训练模型为例子,对自然语言处理的四大下游任务进行介绍
8.2.1 句子对分类任务
-
MNLI
Williams等人[22]提出的多体自然语言推理(Multi-Genre Natural Language Inference)是一项大规模的分类任务。给定一对句子,目标是预测第二个句子相对于第一个句子是包含,矛盾还是中立的。
-
QQP
Chen等人[23]提出的Quora Question Pairs是一个二分类任务,目标是确定在Quora上询问的两个问题在语义上是否等效。
-
QNLI
Wang等人[24]出的Question Natural Language Inference是Stanford Question Answering数据集[25]的一个版本,该数据集已转换为二分类任务。正例是(问题,句子)对,它们确实包含正确答案,而负例是同一段中的(问题,句子),不包含答案。
-
STS-B
Cer等人[26]提出的语义文本相似性基准(The Semantic Textual Similarity Benchmark)是从新闻头条和其他来源提取的句子对的集合。它们用1到5的分数来标注,表示这两个句子在语义上有多相似。
-
MRPC
Dolan等人[27]提出的Microsoft Research Paraphrase Corpus由自动从在线新闻源中提取的句子对组成,并带有人工标注,以说明句子对中的句子在语义上是否等效。
-
RTE
Bentivogli等人[28]提出的识别文本蕴含(Recognizing Textual Entailment)是类似于MNLI的二进制蕴含任务,但是训练数据少得多。
-
SWAG
Zellers等人[29]提出的对抗生成的情境(Situations With Adversarial Generations)数据集包含113k个句子对完整示例,用于评估扎实的常识推理。给定一个句子,任务是在四个选择中选择最合理的连续性。其中,在SWAG数据集上进行微调时,我们根据如下操作构造训练数据:每个输入序列都包含给定句子(句子A)和可能的延续词(句子B)的串联。
-
如图 8.11(a)所示,句子对分类任务首先需要将两个句子用“[SEP]”连接起来,并输入模型。然后,我们给预训练模型添加一个简单的分类层,便可以在下游任务上共同对所有参数进行微调了。具体运算逻辑是引入唯一特定于任务的参数是分类层权重矩阵[W]KxH ,并取BERT的第一个输入标记“[CLS]”对应的最后一层向量[C]H 。通过公式(8.4)计算分类损失loss ,我们就可以进行梯度下降的训练了。
(式-8.4)
其中K为标签种类,H为每个字或者英文单词的隐藏层维度(768)。
8.2.2 单句子分类任务
-
SST-2
Socher等人[30]提出的斯坦福情感树库(Stanford Sentiment Treebank)是一种单句二分类任务,包括从电影评论中提取的句子以及带有其情绪的人类标注。
-
CoLA
Warstadt等人[31]提出的语言可接受性语料库(Corpus of Linguistic Acceptability)也是一个单句二分类任务,目标是预测英语句子在语言上是否“可以接受”。
如图 8.11(b)所示,单句子分类任务可以直接在预训练模型中添加了一个简单的分类层,而后便可在下游任务上共同对所有参数进行微调了。具体运算逻辑如公式(8.4)所示。
8.2.3 问答任务
SQuAD v1.1:Rajpurkar等人[25]提出的斯坦福问答数据集(Stanford Question Answering Dataset)是10万个问题/答案对的集合。给定一个问题以及Wikipedia中包含答案的段落,任务是预测段落中的答案文本范围(start,end)。
到目前为止,所有提出的BERT微调方法都是在预训练模型中添加了一个简单的分类层,并且在下游任务上共同对所有参数进行了微调。然而,并非所有任务都可以轻松地由BERT体系结构表示,因此需要添加特定于任务的模型体系结构。如图 8.11(c)所示,阅读理解任务首先需要将问题和文本用“[SEP]”连接起来,并输入模型。然后,我们再将BERT最后一层向量 [C]LxH 输入到输出层。具体运算逻辑是初始化输出层的权重矩阵[W]KxH ,并通过公式(8.5)计算答案指针概率向量logit。
其中H为隐藏层维度(768),L为序列的长度,K为2,表示logit是个L行2列的矩阵,第1列为答案开头start的指针概率向量,第2列为答案结尾end的指针概率向量。
因为K为2,所以我们能分别抽出答案的开头start_logit和答案end_logit的结尾。并根据两者与真实答案对(start, end)之间的差值计算start_logit和end_logit,最后求出总的loss,如公式(8.6)所示,我们便可以进行梯度下降训练了。
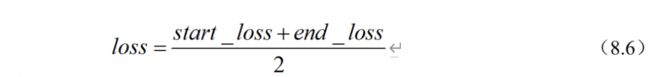
8.2.4 单句子标注任务
单句子标注任务也叫命名实体识别任务(Named Entity Recognition),简称NER,常见的NER数据集有CoNLL-2003 NER[32]等。该任务是指识别文本中具有特定意义的实体,主要包括人名、地名、机构名、专有名词等,以及时间、数量、货币、比例数值等文字。举个例子:“明朝建立于1368年,开国皇帝是朱元璋。介绍完毕!”那么我们可以从这句话中提取出的实体为:
- 机构:明朝
- 时间:1368年
- 人名:朱元璋
同样地,BERT在NER任务上也不能通过添加简单的分类层进行微调,因此我们需要添加特定的体系结构来完成NER任务。不过,在此之前,我们得先了解一下数据集的格式,如图 8.10所示。
它的每一行由一个字及其对应的标注组成,标注采用BIO(B表示实体开头,I表示在实体内部,O表示非实体),句子之间用一个空行隔开。当然了,如果我们处理的是文本含有英文,则标注需采用BIOX,X用于标注英文单词分词之后的非首单词,比如“Playing”在输入BERT模型前会被BERT自带的Tokenization工具分词为“Play”和“# #ing”,此时“Play”会被标注为“O”,则多余出来的“# #ing”会被标注为“X”。
了解完整体的数据格式,我们就开始了解整体的NER任务是如何通过BERT来训练的。如图8.11(d)所示,将BERT最后一层向量 [C]LxH输入到输出层。具体运算逻辑是初始化输出层的权重矩阵[W]KxH ,此时K为1。我们通过公式8.5得到句子的概率向量logit ,进而知道了每一个字或者英文单词的标注概率。然后,我们可以直接通过计算 logit与真实标签之间的差值得到loss ,从而开始梯度下降训练。
当然了,我们也可以将logit 灌入Bi-LSTM进行学习,因为Bi-LSTM能更好地学习文本的上下文关系,最后再下接一个CRF(Conditional Random Field)层拟合真实标签来进行梯度下降训练。
至于为何要加入CRF层,主要是CRF层可以在训练过程中学习到标签的约束条件。比如,“B-ORG I-ORG” 是正确的,而“B-PER I-ORG”则是错误的;“I-PER I-ORG”是错误的,因为命名实体的开头应该是“B-”而不是“I-”,且两个“I-”在同一个实体应该一致。有了这些有用的约束,模型预测的错误序列将会大大减少。
图 8.10 NER数据格式
NLP四大下游任务微调插(图- 8.11)