多智能体强化学习——相关论文
多智能体深度强化学习研究综述
作者:孙 彧,曹 雷,陈希亮,徐志雄,赖 俊
摘 要:多智能体深度强化学习是机器学习领域的一个新兴的研究热点和应用方向,涵盖众多算法、规则、框架,并广泛应用于自动驾驶、能源分配、编队控制、航迹规划、路由规划、社会难题等现实领域,具有极高的研究价值和意义。对多智能体深度强化学习的基本理论、发展历程进行简要的概念介绍;按照无关联型、通信规则型、互相合作型和建模学习型4种分类方式阐述了现有的经典算法;对多智能体深度强化学习算法的实际应用进行了综述,并简单罗列了多智能体深度强化学习的现有测试平台;总结了多智能体深度强化学习在理论、算法和应用方面面临的挑战和未来的发展方向。
传统的MARL 的算法根据其回报函数的不同可以分为完全 合 作 型(Fully Cooperative)、完 全 竞 争 型(Fully Competitive)和混合型(Mixed)三种任务类型。
主流的MDRL,按照智能体之间的通联方式,大致将当前的 MDRL 方法分为:无关联型、通信规则型、互相协作型和建模学习型4大类。

基于强化学习的移动多智能体自组织协同目标搜索
时间:2020年4月
作者:狄小娟 (南京邮电大学)
摘要:本文研究出一种基于强化学习的多智能体系统来实现对目标群体的协同搜索,使其在脱离人工干预的情况下正常运作,对提高多智能体协同合作的搜索效率具有现实意义。本学位论文以多智能体高效协同搜索为目标,在移动自组织网络路由协议改进的基础上结合强化学习的方法以及特殊的搜索覆盖策略来实现。首先设计一种基于优化链路状态协议改进的更适用于多智能体目标搜索任务的自组织网络路由协议,然后设计一种基于传统深度确定性策略梯度算法优化的多智能体协作方法,最后设计一种基于强化学习的移动多智能体区域覆盖搜索策略。
工作创新主要体现在以下三个方面:
1.基于优化链路状态协议改进的更适用于目标搜索场景的多智能体自组织网络路由协议(每个节点选择自己邻居节点中的一部分来作为MPR节点,只允许MPR进行泛洪广播并传播控制消息)。
2.改进的actor-critic嵌入到传统深度确定性策略梯度算法,设计出一种基于深度确定性策略梯度(DDPG)算法改进的移动多智能体协同策略。
3.基于贝叶斯规则的目标更新检测算法,同时设计出一种多智能体区域覆盖搜索算法以使得整个多智能体网络在搜索过程中既能保持连通又能保持搜索的高效性。
基于多智能体强化学习的无人车分布式路径规划方法
时间:2021年
作者:张立雄,郭 艳 *,李 宁,宋晓祥,薛 端(陆军工程大学)
摘要:要求无人车具备自主探索并协同到达多个目标位置的能力。基于此,提出一种基于多智能体强化学习的无人车分布式路径规划模型,通过集中训练方式生成无人车的行驶策略。仿真结果证明了该方法的有效性。
主要工作:
(1)场景设定。在具有多个目标点和障碍物的封闭空间中,假设各无人车可在任意时刻获取环境的状态信息,可基于传感器实时检测车辆与其他障碍物(包括其他车辆)的距离,且各无人车和障碍物的大小是已知的。
(2)路径规划。根据设定的场景,基于不同的路径规划算法,实现无人车对多目标位置的访问。
(3)性能测试。将到达目标位置的成功率和各无人车与目标点的平均距离作为性能指标,对不同路径规划算法的效果进行评估。
在多智能体环境下,通常将强化学习问题扩展为部分可观察的马尔可夫博弈 ,也称作马尔可夫决策过程的多智能体扩展。
该过程可描述为 N 个智能体配置的一组状态 S、动作 A 1 , A 2 , . . . , A N A_1,A_2,..., A_N A1,A2,...,AN 和每个智能体的观察 O 1 , O 2 , . . . , O N O_1,O_2,..., O_N O1,O2,...,ON。每个智能体的初始状态由分布 n确定:S ⟼ \longmapsto ⟼[0,1],在选择动作时采用随机策略 π θ t π_{θ_t} πθt∶ O i × A i ⟼ [ 0 , 1 ] O_i×A_i \longmapsto[0,1] Oi×Ai⟼[0,1],根据状态转移函数产生下一个状态。每个智能体通过状态和动作获得奖励 r i ∶ S × A i ⟼ R r_i ∶ S×A_i\longmapsto R ri∶S×Ai⟼R,并收到与各自状态有关的观察 o i ∶ S i ⟼ O i o_i ∶ S_i \longmapsto O_i oi∶Si⟼Oi,旨在最大化奖励之和 R i = ∑ t = 0 T γ t r i t R_i=∑^T_{t=0}\gamma_tr_i^t Ri=∑t=0Tγtrit ,式中 a是折扣因子,T 是时间范围。
基于值函数逼近的多智能体应用,Q-learning 是 经 典 的 强 化 学 习 算 法,可 以直 接 应 用 于 多 智 能 体 环 境,利 用 动 作 值 函 数 Q π ( s , a ) = E [ R ∣ s ′ = s , a ′ = a ] Q^π(s,a)=E[R|s'=s, a'=a] Qπ(s,a)=E[R∣s′=s,a′=a]生成策略 π。该函数的递归形式为:
![]()
每个智能体单独学习一个最优值函数 Qi并独立更新各自的策略,因此,对于每个智能体来说,环境都会变得不稳定,这将使 Q-learning 达不到收敛所需的马尔可夫假设。
Deep Q Network(简称 DQN)是一种将神经网络和 Q-learning 结合起来的强化学习算法,主要通过最小化损失来学习最优策略对应的动作值函数Q*,其损失函数为:
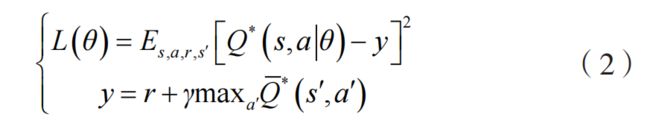
式中: Q ˉ ∗ \bar{Q}^* Qˉ∗ 是目标动作 - 值函数,其参数根据最新的网络参数 θ 周期性更新。DQN 还包含一个经验重放缓冲器 D,其包含元组 (s,a,r,s’),可以打破样本之间的关联性,有助于训练稳定。然而,DQN在用于多智能体的环境时,训练和测试通常不能包含不同的信息。
基于确定性策略搜索的多智能体应用,多智能体深度确定性策略梯度(Multi-Agent
Deep Deterministic Policy Gradient,MADDPG)算法采用集中评估、分布执行的方式,执行时仅依靠智能体的部分观察,无需建立环境模型,不假设有通信环境,算法如下:

相比于 DDPG 算法,MADDPG 算法允许使用一些额外信息(如其他智能体的动作)进行学习。具体体现在:每个智能体的训练同单个 DDPG 算法的训练过程类似,不同之处在于评估网络 Q π Q^π Qπ 的输入。在单个智能体的 DDPG 算法中,评估网络 Q π Q^π Qπ的输入仅仅是一个状态 - 动作信息,但是,在MADDPG 算法中,每个智能体的评估网络 Qπ 的输入除包含自身的状态 - 动作信息外,还包含其他智能体的动作,所利用算法的网络结构如图 2所示。