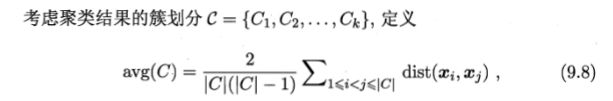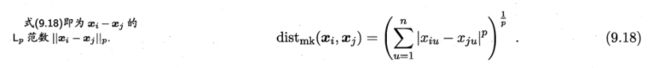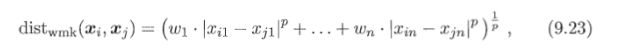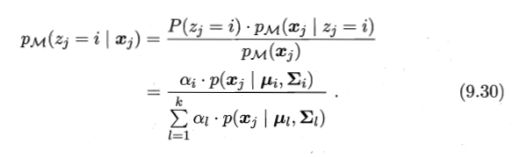西瓜书学习笔记——第九章:聚类
9. 聚类
- 9.1 聚类任务
- 9.2 性能度量
-
- 外部指标:
-
- 定义
- 外部指标
- 内部指标
-
- 定义
-
- 簇内样本平均距离avg( C)
- 簇内样本间最远距离diam( C )
- 簇间最近样本距离$d_{min}(C)$
- 簇中心间距$d_{cen}(C_i,C_j)$
- 内部指标
- 9.3 距离计算
-
- 闵可夫斯基距离(Minkowski distance)
- 曼哈顿距离(街区距离)
- 欧氏距离
- 切比雪夫距离
- 根据属性的性质选择采用的距离
-
- 有序属性
- 无序属性
- 混合属性(有序+无序:闵可夫斯基距离和VDM结合)
- 属性重要性不同(加权距离)
- 9.4 原型聚类
-
- 9.4.1 k均值算法(k-means聚类)
- 9.4.2 学习向量量化
- 9.4.3 高斯混合聚类
-
- 1.定义高斯混合分布
- 2.样本生成过程
- 3.EM法迭代优化求解
- 将样本划分簇
- 高斯混合聚类算法过程
- 9.5 密度聚类
-
- DBSCAN算法
-
- 一些概念
- 簇的定义
- 算法过程
- 9.6 层次聚类
-
- AGNES算法
- AGNES算法过程
9.1 聚类任务
聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个簇(cluster)。但需注意的是,聚类过程仅能自动形成簇结构,簇所对应的概念语义需由使用者来把握和命名。
聚类既能作为一个单独的过程,用于寻找数据内在的分布结构,也可作为分类等其他学习任务的前驱过程。
9.2 性能度量
聚类性能度量也称聚类有效性指标(validity index),与监督学习中的性能度量作用类似。
- 对聚类结果,需要通过某种性能度量来评估其好坏。
- 若明确了最终将要使用的性能度量,则可直接将其作为聚类过程的优化目标。
对于聚类,一般通用的度量标准为“物以类聚”,即:簇内相似度高且簇间相似度低。
两类性能度量:
- 外部指标:将聚类结果与某个参考模型(如将领域专家给出的划分结果作为参考模型)进行比较
- 内部指标:直接考察聚类结果而不利用任何参考模型
外部指标:
定义
外部指标
- Rand指数(Rand Index,简称RI)
(9.7) R I = a + d C m 2 RI=\dfrac{a+d}{C_m^2}\tag{9.7} RI=Cm2a+d(9.7)
a + b a+b a+b表示与参考模型划分结果一致的样本数量
注:以上指数取值范围为[0,1],且越大越好
内部指标
定义
簇内样本平均距离avg( C)
簇内样本间最远距离diam( C )
簇间最近样本距离 d m i n ( C ) d_{min}(C) dmin(C)
簇中心间距 d c e n ( C i , C j ) d_{cen}(C_i,C_j) dcen(Ci,Cj)
![]()
μ i \mu_i μi表示簇 C i C_i Ci的中心点
内部指标
- 对于式(9.12)的分子(簇内平均距离),应越小越好,分母则是越大越好,故整体DBI应越小越好
- 对于式(9.13)的分子(最小簇间距离)应越大越好,分母(簇内样本最大距离)应越小越好,故整体DI应越大越好
9.3 距离计算

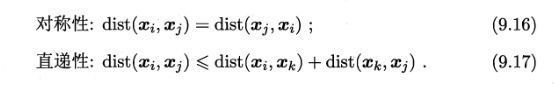
注:直递性常被直接称为“三角不等式”,不满足直递性的距离称为非度量距离,对于某些现实任务,我们不能使用定义好的距离公式,而是需要我们基于数据样本来确定合适的距离计算式,这可通过距离度量学习来实现
闵可夫斯基距离(Minkowski distance)
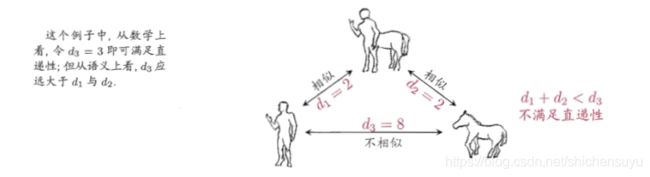
曼哈顿距离(街区距离)
当闵可夫斯基距离表达式的 p = 1 p=1 p=1时,即为曼哈顿距离的表达式:
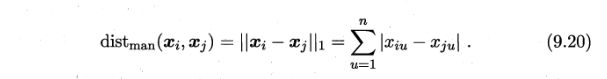
欧氏距离
当闵可夫斯基距离表达式的 p = 2 p=2 p=2时,即为欧氏距离的表达式:
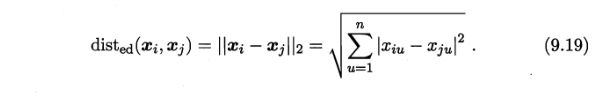
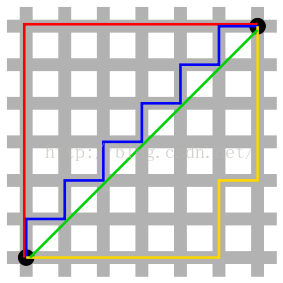
注:红蓝黄都为曼哈顿距离,绿色为欧氏距离
切比雪夫距离
维基百科对切比雪夫距离的定义:
数学上,切比雪夫距离(Chebyshev distance)或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各坐标数值差的最大值。
二维平面上两点a(x1,y1),b(x2,y2)之间的切比雪夫距离公式:
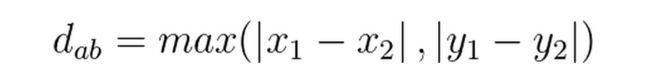
n维空间上两点a(x1,x2,…,xn),b(y1,y2,…,yn)的切比雪夫距离公式:
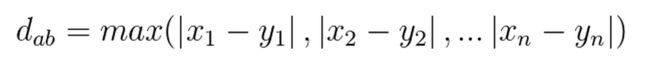
根据属性的性质选择采用的距离
有序属性
如{小,中,大},“小”与“中”较近,与“大”较远。显然,闵可夫斯基距离可用于有序属性。
无序属性
如{飞机,火车,轮船}这样的离散属性则不能直接在属性上直接计算距离,称为无序属性。

如:要计算对于出行方式这个属性上飞机和火车这两个离散值的VDM距离,即为:
∑ i = 1 k ∣ 在 簇 i 中 出 行 方 式 为 飞 机 的 人 数 出 行 方 式 为 飞 机 的 总 人 数 − 在 簇 i 中 出 行 方 式 为 火 车 的 人 数 出 行 方 式 为 火 车 的 总 人 数 ∣ \sum_{i=1}^{k}|\dfrac{在簇i中出行方式为飞机的人数}{出行方式为飞机的总人数}-\dfrac{在簇i中出行方式为火车的人数}{出行方式为火车的总人数}| i=1∑k∣出行方式为飞机的总人数在簇i中出行方式为飞机的人数−出行方式为火车的总人数在簇i中出行方式为火车的人数∣
混合属性(有序+无序:闵可夫斯基距离和VDM结合)
属性重要性不同(加权距离)
9.4 原型聚类
原型:样本空间中具有代表性的点
原型聚类也称基于原型的聚类(prototype-based clustering),此类算法假设聚类结构能通过一组原型刻画。采用不同的原型表示、不同的求解方式,将产生不同的算法。
9.4.1 k均值算法(k-means聚类)

k-means聚类算法过程:

对于簇中心的迭代停止条件为:达到最大迭代轮数或调整幅度小于最小调整幅度阈值
9.4.2 学习向量量化
学习向量量化(Learning Vector Quantization,LVQ)同k-means聚类类似,也是试图找到一组原型向量来刻画聚类结构。不同的是,LVQ针对于带有类别标记的数据样本,学习过程利用样本的监督信息(类别标记)来辅助聚类。

注:停止条件为达到最大迭代轮数或原型向量更新很小甚至不再更新
上面的算法过程6-10行对应着如何更新原型向量。直观上看,对样本 x j x_j xj,若最近的原型向量 p i ∗ p_{i*} pi∗与 x j x_j xj的类别标记相同,则令 p i ∗ p_{i*} pi∗向 x j x_j xj的方向靠拢,如第7行所示,此时新原型向量为:
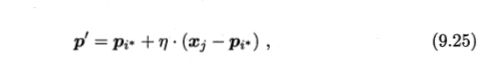
即产生一个新的 p i ∗ p_{i*} pi∗,它距离样本 x j x_j xj更近
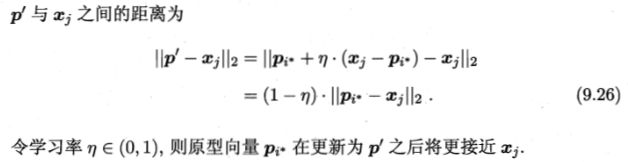
9.4.3 高斯混合聚类
与k-means、LVQ用原型向量来刻画聚类结构不同,高斯混合聚类采用概率模型来表达聚类原型。

注:一元高斯分布的概率密度函数为:
p ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 p(x)=\dfrac{1}{\sqrt{2\pi} \sigma}e^{-\dfrac{(x-\mu)^2}{2\sigma^2}} p(x)=2πσ1e−2σ2(x−μ)2
1.定义高斯混合分布
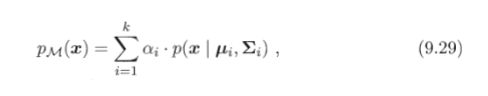
该分布共由k个混合成分组成,每个混合成分对应一个高斯分布;
α i > 0 \alpha_i>0 αi>0为混合系数,且 ∑ i = 1 k α i = 1 \sum_{i=1}^k\alpha_i=1 ∑i=1kαi=1,混合系数也为选择第i个混合成分的概率。
2.样本生成过程
- 被选中的高斯混合分布的参数为 μ i \mu_i μi和 ∑ i \sum_i ∑i代入式(9.28)即可求出对应的概率密度 p ( x ∣ μ i , ∑ i ) p(x|\mu_i,\sum_i) p(x∣μi,∑i)
- 样本 x j x_j xj出现的概率为 p M ( x j ) p_M(x_j) pM(xj)
- P ( z j = i ) = α i P(z_j=i)=\alpha_i P(zj=i)=αi
- p M ( z j = i ∣ x j ) p_M(z_j=i|x_j) pM(zj=i∣xj):样本 x j x_j xj由第 i i i个高斯混合成分生成的后验概率,简写为 γ j i \gamma_{ji} γji
3.EM法迭代优化求解
利用EM算法迭代更新式(9.29)的模型参数 { α i , μ i , ∑ i ∣ 1 ≤ i ≤ k } \{\alpha_i,\mu_i,\sum_i|1\leq i\leq k\} { αi,μi,∑i∣1≤i≤k}才能计算出新的式(9.30)的结果用于下轮的迭代计算。
求解模型参数,我们可以使用MLE,似然函数为各个样本出现概率的乘积,为了防止连乘溢出,通常我们计算的是最大化对数似然:
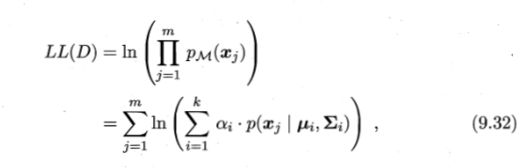
分别对 μ i , ∑ i \mu_i,\sum_i μi,∑i求导,并令其导数为0,得:

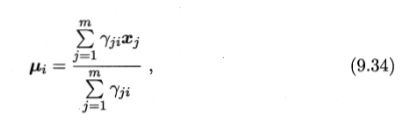
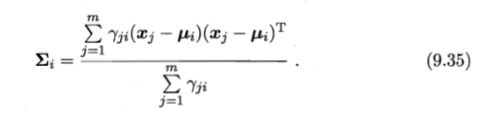
而对于混合系数 α i \alpha_i αi,除了要最大化对数似然,还要满足约束条件 α i > 0 , ∑ i = 1 k α i = 1 \alpha_i>0,\sum_{i=1}^k\alpha_i=1 αi>0,∑i=1kαi=1,可以采用拉格朗日乘数法进行求解, L L ( D ) LL(D) LL(D)的拉格朗日形式为:
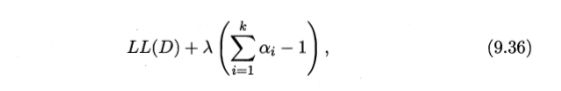


将样本划分簇
当EM迭代优化轮数到达停止条件,就可以按照最终模型得到各个样本 x j x_j xj的后验概率 p M ( z j = i ∣ x j ) p_M(z_j=i|x_j) pM(zj=i∣xj),也即得到 γ j i \gamma_{ji} γji

注:对每个样本 x j x_j xj对应的 λ j \lambda_j λj的确定,即计算对于样本 x j x_j xj,当 i = 1 , 2 , . . . , k i=1,2,...,k i=1,2,...,k时的 p M ( z j = i ∣ x j ) p_M(z_j=i|x_j) pM(zj=i∣xj),最大的那一个 γ j i \gamma_{ji} γji即为该样本的 λ j \lambda_j λj
这样,就完成了对每个样本的簇划分。
高斯混合聚类算法过程
9.5 密度聚类
密度聚类也称基于密度的聚类,此类算法假设聚类结构能通过样本分布的紧密程度确定(原型聚类是假设聚类结构能够通过一组原型刻画)。
通常情况下,密度聚类算法从样本密度角度来考察样本间的可连接性(密度直达,密度可达,密度相连),并基于可连接样本来不断拓展聚类簇。
DBSCAN算法
一些概念
该算法基于一组邻域参数 ( ϵ , M i n P t s ) (\epsilon,MinPts) (ϵ,MinPts)来刻画样本分布的紧密程度。
给定数据集 D = { x 1 , x 2 , . . . , x m } D=\{x_1,x_2,...,x_m\} D={ x1,x2,...,xm},定义以下概念:

注:距离为欧氏距离

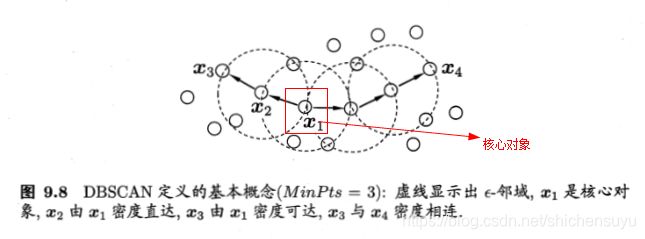
- 直达:在同一个 ϵ \epsilon ϵ-邻域
- 可达:间接可达,不在同一个 ϵ \epsilon ϵ-邻域
簇的定义
基于上面的概念,DBSCAN将簇定义为:由密度可达关系导出的最大密度相连样本集合。对于D中不属于任何簇的样本,会被视为噪声或异常样本。
算法过程
9.6 层次聚类
层次聚类试图在不同层次对数据集进行划分,从而形成树形的聚类结构。
对于数据集的划分,层次聚类通常有两种策略:
- 自底向上的聚合策略
- 自上而下的分拆策略
AGNES算法
AGNES是一种采用自底向上聚合策略的层次聚类算法。算法的基本过程是:先将每个样本都看做一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直到到达预设的聚类簇个数。
对于簇间距离的计算,可通过以下式子计算 C i 和 C j C_i和C_j Ci和Cj之间的距离:
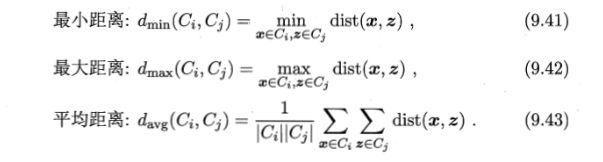
显然,可以看出:
- 簇间最小距离由两个簇的最近样本决定
- 簇间最大距离由两个簇的最远样本决定
- 平均距离由两个簇的所有样本决定
当聚类簇的距离由 d m i n 、 d m a x 或 d a v g d_{min}、d_{max}或d_{avg} dmin、dmax或davg计算时,AGNES算法被相应地称为单链接、全链接或均链接算法。