详解记录历史的可持久化数据结构

文本编辑器里的 "undo" 和 "redo"，数据库系统的 MVCC，git 的历史记录，mac 的
Time Machine，等等功能，他们都有一个共同点，就是记录历史。这个功能依赖一种数据结
构：持久化数据结构 (Persistent data structure)。持久化数据结构记录所有历史版本，
你可以读取任意版本的数据。

原文地址

"持久化" 的含义

"持久化(persistence)" 是指拥有查询数据历史版本的能力，它有以下4个级别：

1. 半持久化 (Partial Persistance) - 可以读数据结构过去任意版本，只能在最新版本
   写。
2. 全持久化 (Full Persistance) - 可以读数据结构过去任意版本，可以在数据结构任意
   版本写。
3. 可合并持久化 (Confluent Persistent) - 不光可以在任何版本上读写，还可以将两个版
   本合并以创建一个新的版本。
4. 函数式持久化 (Functional Persistance) - 函数式编程中实现的持久化数据结构，对
   象都是只读的，任意修改都是创建一个新的节点，而不是在旧节点上修改。参考
   Puerly functional data structure。

以上四种持久化是逐步增强的，函数式持久化包含可合并持久化，合并持久化包含全持久化，
全持久化包含半持久化。函数式持久化包含合并持久化是因为在函数式持久化中我们只限制
了实现方式。如果在合并持久化中我们不允许合并，那么它就是全持久化。在全持久化中限
制只能在最新版本上写，它就变成了半持久化。

4种持久化示意图如下所示。

半持久化就像是 undo 和 redo，它是线性的记录历史。 全持久化就像是 emacs 上的
undo-tree，它记录了分支。合并持久化就像是 gitflow，它允许分支与合并操作。

gitflow:

半持久化数据结构

先看半持久化链表的实现，很容易扩展出其他数据结构半持久化版本。

半持久化链表的实现方法

正常链表节点包含三个成员： (val, next, prev)， val 表示节点值，next 指向链表下一
个节点， prev 指向链表上一个节点。 要实现半持久化，还需要一个区域 mods，用来保存
节点的修改历史。

(1) 写操作, new_version = write(node, variable, value)

半持久化写操作参数为变量，目标值，返回版本号。

如果节点 n 的 mods 区域没有满，还能容纳新的修改历史，就把修改历史直接写到
mods 区域。

如果节点 n 已经的 mods 区域已经写满了，再也不能容纳新的修改历史了：

• 新建节点 n' 。
• 将节点 n 的最新值 (包括 val, next, prev) 复制到 n' 。
• 对所有 n 指向的节点 x (x=n->next)，修改反向指针指向 n'
  ( x->prev=n' )。
• 对于所有拥有指针指向 n 的节点 x ( x->next=n )，递归的调用
  write(x, next, n') 。

(2) 读操作， read(node, variable, version)

读操作 read(node, var, v) 查询 mods 记录，找到版本最大的记录版本 \( w \) 使得
\( w\leq v \) ， 版本修改记录 \( w \) 中的值就是要查询的值。

以上述链表为例，要修改第二个节点 v1=write(node2, val, 20) ，只需要添加 mods 修改历史，如
图所示。

再多加几次修改:

v2=write(node2,val,33)
v3=write(node2,val,50)    
v4=write(node2,val,21)

结构如下图， mods 区域已经写满了。

记没修改过的初始值为 v0 。
要查询这个链表 v3 版本，从根节点开始： (val,v0)=1,(next,v0)=node2 ； node2
节点查询到满足 \( \leq v3 \) 的版本 (val,v3)=50,(next,v0)=node3,(prev,v0)=node1 ;
node3 节点查询到满足 \( \leq v3 \) 的版本
(val,v0)=3,(next,v0)=nullptr,(prev,v0)=node2 。得知链表在版本 v3 为
<1,50,3> 。

再修改 node2 的值 v5=write(node2,val,200) ，此时 mods 已经满了，需要新建节
点 new_node2 ：

此时查询链表版本 v5 ， 从根节点开始： (val,v0)=1,(next,v5)=new_node2 ; new\_node2
节点 (val,v0)=200,(next,v0)=node3 ， node3 节点 (val,v0)=3,(next,v0)=nullptr
。得知链表版本 v5 为 <1,200,3> 。

不难看出如果 write() 方法要递归修改多处，均修改完成后返回版本的最大值。

使用类似的方法，可以实现半持久化二叉树等数据结构。 基本数据结构都可以使用节点和
指针来表示，稍作变化就可以半持久化几乎所有基本数据结构。

更一般的半持久化数据结构

链表、树、图可以抽象为 Pointer Machine 。我们扩展 Pointer Machine，将其变成半持
久化数据结构，这样就相当于扩展了任意基础数据结构。

只考虑入度确定的 Pointer Machine，设入度为 \( p \) , 如上图所示，每个节点有三类成员。

1. 只读的数据成员，共 \( d \) 个数据成员。 这是原有数据结构本来就存在的，数据成员包
   括数值和指针。
2. 可写的反向指针区域 (back pointers)。这些反向指针能告诉我们哪些节点的数据成员
   指向了当前节点。入度是 \( p \) 所以反向指针成员数量为 \( p \) 。
3. 可写的修改历史区域 (mods)。保存对节点数据成员的修改，内容结构是
   (field,version)=value 。注意修改反向指针并不需记录 mods 。

实现任意节点的读写操作如下：

1. read(node, field, version) - 在节点的修改记录区 node.mods 查找修改 field
   成员的最大版本 \( w \) ， 使得 \( w\leq version \) 。 如果没找到，那么只读的数据成员
   区域的 field 成员就是当前值。

2. write(node, field, value) - 如果 node.mods 没满，就向其中添加一个记录
   (field,version)=value 。如果 node.mods 满了：

   • [新建节点] node'
   • [设置最新值] 将旧节点的数据成员区域(数据和指针)的最新值复制到 node' 的数据成员区域。
   • [修改其他节点的反向指针] 任意 node 指向的节点 x ， 修改 x 的反向指针指向新节点 node' 。
   • [递归修改其他节点的指针成员] 任意指向 node 的节点 x , 递归调用
     write(x, pointer_to_node, node') 使得最新版本的指针指向新节点。

演示半持久化二叉树实现如下图。

半持久化数据结构的时间复杂度

我们只考虑度数是指定常数的数据结构。节点入度数为 \( p \) , 令节点的 mods 的最大记
录数量为 \( 2p \) 。

读操作 read(node, field, version) 是很快的，只需要读取 node.mods ， \( O(1) \) 。
写操作 write(node, field, value) 有两种情况，如果节点没满，直接写入一个修改日
志，复杂度是 \( O(1) \) ； 如果节点满了，可能会递归调用 write() 修改指针：

$$ cost(n) = c + \sum_{all\ node\ x\ point\ to\ n}\left(cost(x)\right) $$

其中 \( c \) 表示新建一个节点并复制旧节点数据，修改反向指针的 \( O(1) \) 操作。递归步骤
是很贵的，但只有节点满的时候才会执行递归操作，然后节点又会变空，直到节点变满之前
都不会引起递归操作。平均下来 write() 耗时很少。 我们使用摊还分析
(amortize analysis) 来计算写操作的事件复杂度。

设势能函数 \( \phi \) ， 每次操作的摊还代价等于这次操作的实际代价加上此操作引起的势
能变化：

$$ amortized\_cost(n) = cost(n) + \Delta\phi $$

势能函数为：

$$ \phi = c\times (mods\ number) $$

节点之前是满的，后来空了，所以势能变化为 \( -2cp \) 。

$$ amortized\_cost(n) \leq c + c - 2cp + p \times amortized\_cost(x) $$

对于节点 \( x \) ， 公式中第二个 \( c \) 是找到 mods 对应位置并添加个记录的次数，所以
造成势能增加 \( c \) 。

将右边展开容易的出均摊复杂度是 \( O(1) \) 。
更详细的分析见此文档。

全持久化数据结构

全持久化版本号的问题

在半持久化数据结构中，版本是线性的、全序的，版本号使用数字就可以，数字大小表现了
版本的新旧关系。全持久化可以修改任意版本，它的版本变化形成树形结构，版本是个偏序
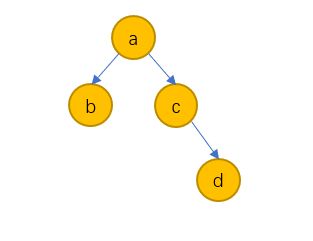
关系，并不是任意两个版本都可以比较的。如下图，版本 \( a \) 和版本 \( b \) 的关系是 \( a，但版本 \( b \) 和版本 \( d \) 是不可比较的。因此版本使用数字大小来代表就不合适了，全持
久化中的版本只是一个标识，他的序关系只能在版本树中展示，这意味着每次比较版本号都
执行一个 \( O(n) \) 操作。

幸运的是，树形结构可以通过中序遍历的顺序转化为线性结构，中序遍历过程中记录每个节
点初次访问和末次访问的顺序。如上图的树，线性表示为：

$$ b_{a}b_{b}e_{b}b_{c}b_{d}e_{d}e_{c}e_{a} $$

\( b_{a} \) 表示初次访问节点 \( a \) ， \( e_{a} \) 表示末次访问节点 \( a \) 。这样，就很容易判
断后继、前序的关系，例如 \( b_{c}>b_{d}>e_{d}>e_{c} \) 可知 \( d \) 是 \( c \) 的后继。
有一个数据结构
order maintenance 可以在 \( O(1) \) 的时间复杂度上实现这个版本号序的解答。这样就可以
在 \( O(1) \) 时间内解答版本 \( v \) 是否是版本 \( w \) 的后继。

全持久化数据结构实现

如下图所示，全持久化的数据结构与半持久化数据结构类似。同样值考虑入度为 \( p \) 的数
据结构。每个节点存储 \( d \) 个成员 (包括数据和指针)， \( p \) 个反向指针， 注意出度也受
到成员数量 \( d \) 的限制。 mods 区域大小增加到 \( 2(d+p+1) \) ， mods 除了保存数据
成员的修改，也要保存反向指针的修改。

实现读写操作如下。

1. read(node, field, version) - 在 mods 中使用 order-maintenance 结构找到
   \( version \) 或它的最近前驱，返回其值。

2. write(node, field, value, version) - 如果 node.mods 还有空间，就添加一个
   记录 (field,version_next)=value ， 其中 \( version_next>version \) 。如果
   node.mods 满了：

   • [以版本 \( k \) 为界切分子树] 新建节点 \( m \) 。将节点 \( node \) 的 mods 记录分为两
     份，使得存在某个版本 \( k \) 和它的的所有后继都在其中一份，另一份中不包含 \( k \)
     或任何 \( k \) 的后继。
     新节点 \( m \) 保存所有 \( k \) 的后继的 mods ；老节点 \( node \) 保存其它的。
     如下图所示。
   • [保存版本 \( k \) 的值] 计算老节点 \( node \) 的最近 \( m \) 的前驱版本所有数据和反向指
     针，复制到 \( m \) 的数据区。
   • [修改指针] 递归调用 write() 更新所有邻居的指针(正向和反向)，最多需要更新
     \( d+p+(d+p+1) \) 次。

全持久化数据结构的时间复杂度

显然读操作复杂度是 \( O(1) \) 。

写操作如果不切分节点的话是 \( O(1) \) ， 如果要切分节点就比较复杂。同样使用 amortize
技术：

$$ \phi = -c(numer\ of\ empty\ mods) $$

势能函数是 mods 空间数量的负数（其实每次操作的势能变化都加上 mods 空间总量就
是 mods 记录数，与半持久化时一样）。 如果切分 \( \Delta\phi = -2c(d+p+1) \) 否则
\( \Delta\phi=c \) 。所以

$$ amortized\_cost(n) \leq c + c - 2c(d+p+1)+(d+p+(d+p+1))*amortized_cost(x) $$

展开后常数部分消失了，所以写操作是 \( O(1) \) 。

合并持久化数据结构

实现方法可以参照以上全持久化数据结构。版本从树结构变成了有向无环图，但是偏序关系
仍在。

合并操作很麻烦，比如说某个版本，自己跟自己合并， 合并后的新版本再跟自己合并，
这样合并 \( n \) 次之后版本就有 \( 2^{n} \) 了。

可合并持久化数据结构的时间复杂度分析很麻烦，每种特定的数据结构可以定义自己的合并
操作，就可能出现不同的时间复杂度。
具体参考 Making Data Structures Confluently Persistent。

函数式持久化数据结构

相比与前述结构，它只规定了使用函数式方法来实现。有几个成熟的数据结构实现了函数式
持久化：

• 二叉树 (Functional balanced BST) - 主要是复制一份要修改的节点，并把它的前驱节
  点都复制一份因为要修改。
  Confluently Persistent Tries for Efficient Version Control 这篇文章实现了
  \( O(log(n)) \) 的函数式持久化实现。

  

• 列表 - Purely Functional Worst Case Constant Time Catenable Sorted Lists 实现
  了这个数据结构的函数式持久化。

可以参照这几个数据结构实现函数式持久化的其他数据结构。