sklearn机器学习(五)线性回归算法测算房价
本文的数据集使用的是sklearn自带的波士顿房价数据集。
一个地方的房价会受到很多因素的影响,这些因素对应的就是输入矩阵中的特征。而本波士顿的数据集中记录房价主要是受到了十三个因素的影响,故输入矩阵的特征也为13个。分别为
在scikit-learn中的房价数据集里,总共收集了13个特征
CRIM:城镇人均犯罪率
ZN:城镇超过25000平方英尺的住宅区域的占地比例
INDUS:城镇非零售用占地比例
CHAS:是否靠近河边,1靠近,0远离
NOX:一氧化氮浓度
RM:每套房产的平均房间个数
AGE:1940年之前盖好,且业主自住的房子比例
DIS:与波士顿市中心的距离
RAD:周边高速公道的便利性指数
TAX:每10000美元的财产税率
PTRATIO:小学老师的比例
B:城镇黑人比例
LSTAT:地位较低的人口比例
以上数据采集自1996年的波士顿房价数据。
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
boston=load_boston()#波士顿的房价数据集
X=boston.data#一共506个拥有13个特征的数据
y=boston.target#(506,1)的数组,对应房价的数值
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2,random_state=3)#划分数据集,80%作为训练集,20%作为测试集
输入X[0]能够看到十三个特征的数值,boston.feature_names可以看到十三个特征的名字。作者输入了y[0],得到的输出为24,应该就是当时的房价。对比一下现在中国的房价。。。。。。。。
以下是数据集的整理与划分
import time#引入时间
from sklearn.linear_model import LinearRegression
model=LinearRegression()#生成线性回归模型
start=time.clock()#记录时间
model.fit(X_train,y_train)#训练模型
train_score=model.score(X_train,y_train)#得到训练集的分数
cv_score=model.score(X_test,y_test)#得到测试集的分数
print('elaspe:{0:0.6f};train_score:{1:0.6f};cv_score:{2:.6f}'.format(time.clock()-start,train_score,cv_score))#输出
输出如下:elaspe:0.002321;train_score:0.723941;cv_score:0.795262
elaspe是程序运行时间,就是程序的效率;train_score是训练集得分,得分0.723941,明显处欠拟合的状态,cv_score是test集得分,观察可得出是否过拟合。
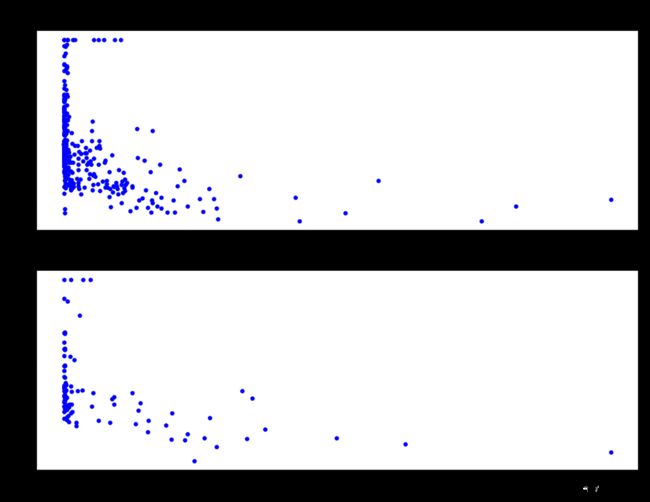
另外处于好奇心,我看了一下数据训练集与测试集中,房价与犯罪率的对比图,代码图例如下:
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6),dpi=144)
plt.subplot(2,1,1)
plt.title("Target and CRIM Train")
plt.scatter(X_train[:,0],y_train,c='b',s=5)
plt.subplot(2,1,2)
plt.title("Target and CRIM test")
plt.scatter(X_test[:,0],y_test,c='b',s=5)
plt.show()
接下来将一些优化政策。
首先是将上面的数据进行归一化处理。其实就只需要改一句
model=LinearRegression(normalize=True)#改一句就好
这是改了之后的输出:elaspe:0.002477;train_score:0.723941;cv_score:0.795262
可是我发现这个效率怎么好像还低了啊!咱也不敢说,咱也不敢问。
有大佬能帮忙解释一下最好!
然后就是再来建立一个流水线的生产模型,在前面已经备注得很详细,这里就不多说。
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
def polynomial_model (degree=1):
polynomial_features=PolynomialFeatures(degree=degree,include_bias=False)
linear_regression=LinearRegression(normalize=True)
pipeline=Pipeline([("polynomial_features",polynomial_features),("linear_regresssion",linear_regression)])
return pipeline
下面是使用2阶多项式来进行拟合:
model=polynomial_model(degree=2)
start=time.clock()
model.fit(X_train,y_train)
train_score=model.score(X_train,y_train)
cv_score=model.score(X_test,y_test)
print('elaspe:{0:0.6f};train_score:{1:0.6f};cv_score:{2:0.6f}'.format(time.clock()-start,train_score,cv_score))
结果如下:
elaspe:0.125763;train_score:0.930547;cv_score:0.860049
从上可以发现花费的时间上升,训练集与测试集的分数得到了明显的提升。因此上面应该是欠拟合了。
接下来,换成三阶多项式尝试一下:
model=polynomial_model(degree=3)
输出如下:
elaspe:3.007593;train_score:1.000000;cv_score:-107.295951
从上可以看出,首先时间效率上出现很大的浪费,其次训练集的分数竟然达到了1.0,而测试集却是负数。明显这是过拟合的状态。
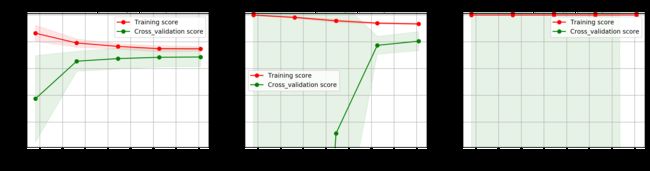
下面就是进行学习曲线的绘制。
首先我们需要把前面的学习曲线函数给拿过来。
还是贴在这里吧!
学习曲线
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
import numpy as np
import matplotlib.pyplot as plt
def plot_learning_curve(estimator,title,X,y,ylim=None,cv=None,n_jobs=1,train_sizes=np.linspace(0.1,1.0,5)):
plt.title(title)#图像标题
if ylim is not None:#y轴限制不为空时
plt.ylim(*ylim)
plt.xlabel("Training examples")#两个标题
plt.ylabel("Score")
train_sizes,train_scores,test_scores=learning_curve(estimator,X,y,cv=cv,n_jobs=n_jobs,train_sizes=train_sizes)#获取训练集大小,训练得分集合,测试得分集合
train_scores_mean=np.mean(train_scores,axis=1)#将训练得分集合按行的到平均值
train_scores_std=np.std(train_scores,axis=1)#计算训练矩阵的标准方差
test_scores_mean=np.mean(test_scores,axis=1)
test_scores_std=np.std(test_scores,axis=1)
plt.grid()#背景设置为网格线
plt.fill_between(train_sizes,train_scores_mean-train_scores_std,train_scores_mean+train_scores_std,alpha=0.1,color='r')
# plt.fill_between()函数会把模型准确性的平均值的上下方差的空间里用颜色填充。
plt.fill_between(train_sizes,test_scores_mean-test_scores_std,test_scores_mean+test_scores_std,alpha=0.1,color='g')
plt.plot(train_sizes,train_scores_mean,'o-',color='r',label='Training score')
# 然后用plt.plot()函数画出模型准确性的平均值
plt.plot(train_sizes,test_scores_mean,'o-',color='g',label='Cross_validation score')
plt.legend(loc='best')#显示图例
return plt
之后是绘制
cv=ShuffleSplit(n_splits=10,test_size=0.2,random_state=0)#这是交叉验证类迭代十次
#plt.figure(figsize=(18,4),dpi=200)
title=("Learning curve (degree={0})")
degrees=[1,2,3]
start=time.clock()#开始计时
plt.figure(figsize=(18,4),dpi=200)
for i in range(len(degrees)):
plt.subplot(1,3,i+1)
plot_learning_curve(polynomial_model(degrees[i]),title.format(degrees[i]),X,y,ylim=(0.01,1.01),cv=cv)
print('elaspe:{0:.6f}'.format(time.clock()-start))#运行的时间