机器学习基础篇（五）——决策树

机器学习基础篇（五）——决策树

一、简介

决策树是机器学习的一种分类器算法（特定情况也可以用于回归），基于特征对实例进行分类的过程，可以认为是if-then的集合。
决策树的思想很简单，类似于我们平时做选择的过程，为了方便理解，让我们模拟一个现实情境：
假如你是Mike，你在考虑自己在某一天是否要去商场购物，你会基于什么信息做出是否购物的决定？
你可能会考虑自己的家里物品的存量是不是足够用，会考虑到当天的天气是好是坏，也可能要考虑当天是否需要上班。Mike会基于这些因素，来判断当天是否去购物。下图是Mike是否购物的一个决策示例：

通过图示数据，我们可以理解Mike在什么情况下会购物，并且用这个方法判断Mike以后是否会去购物。首先我们将第一因素划分成一个决策树，如图：

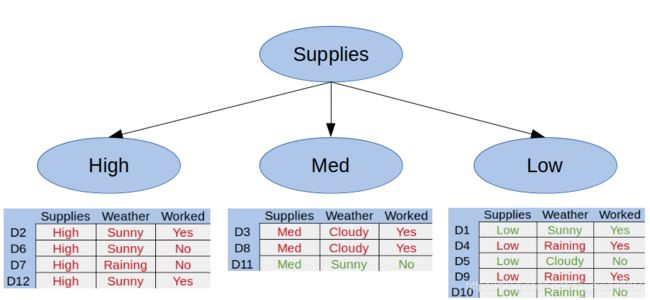
从图中我们可以发现，当Mike家里物品的供应量足够高时，无论其他条件如何，他都不会去购物，这种情况被称为纯子集。
纯子集：仅仅具有正例或者仅仅具有反例的子集。
下图是Mike在这天是否工作的情况：

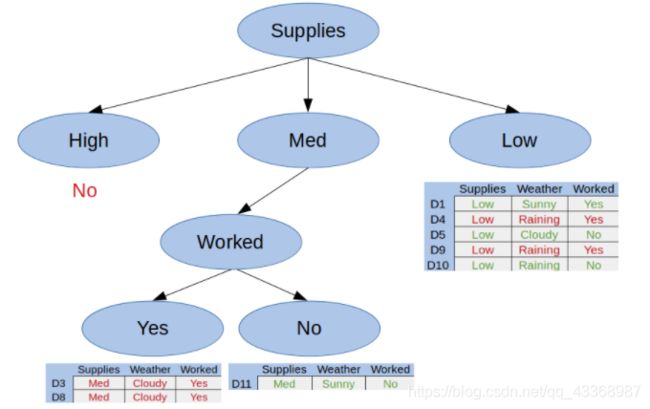
如图所示，当物品的存量中等的时候，根据是否工作，我们可以得出两个纯子集，即当物品存量始终的时候：工作，就不去购物；不工作，就去购物。所以在这个分支中我们得到了一个完整的分枝树。最后，让我们看看当天的天气对Mike是否购物的影响，如图：

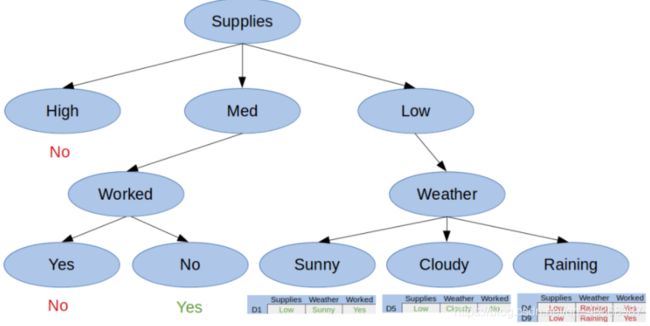
现在我们拥有了所有的纯子集，可以根据此创建一个完整的决策树了，如图：

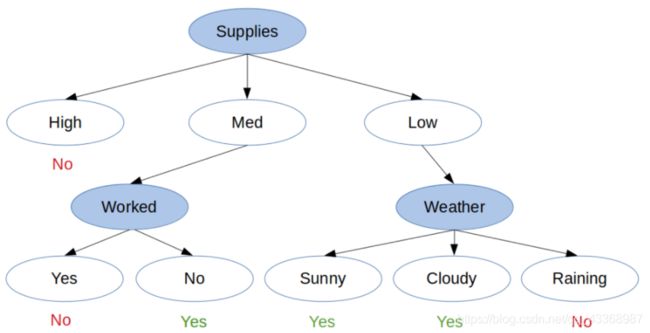
我们可以很简单的创建，解释和可视化一个决策树。决策树的层次结构和分类特征决定了决策树可以非常直观的展现出我们的选择，因此，在数据建模的过程中，我们通常首先会选择决策树的算法。在决策的每个结点，我们都能够确切的看到我们的模型做出了什么决定。在实践中，我们将能够完全理解我们的准确度和误差来自何处，模型可以很好地处理哪种类型的数据，以及输出如何受到特征值的影响。

二、分类树和回归树

决策树的常见算法有CART,ID3,C4.5等算法，这些算法分别被用于分类和回归问题。分类树如上，最终在一组可能的值中选取结果，而回归树的结果是连续的，例如商品的价格。

三、决策树的分裂

我们应该如何构建一棵决策树？
决策树的构建是数据逐步分裂的过程，我们需要一种递归算法来确定我们所要分裂的最佳特征，常见的一种算法是贪心算法

该算法的构建的步骤：

1. 将所有的特征看成一个一个节点
2. 遍历所有特征的所有分割方式，找到最好的分割点，将数据化分为不同的子节点，计算划分后子节点的纯度信息
3. 寻找最优的特征以及最优化分方式，按照该条件对当前数据集进行分割操作，形成子节点
4. 对子女的子节点执行2—3步，知道每个最终的子节点都足够纯

决策树算法构建的停止条件：

1. （会导致过拟合）当子节点中只有一种类型的时候停止构建（此时该节点纯度最高）
2. （比较常用）当前节点样本值小于某个值，同时迭代次数达到指定值，停止构建，此时使用该节点中出现最多的类别样本数据作为对应值
   注：纯度可以理解为目标样本分的足够开的程度，可以用cost函数来衡量

四、基尼指数

我们可以运用基尼指数来衡量样本的纯度
基尼指数： 表示在样本集合中一个随机选中的样本被分错的概率
（基尼指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯）
基尼指数的算法：基尼指数=样本被选中的概率*样本被选错的概率

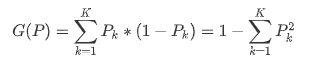
Pk表示选中的样本属于k类别的额概率，则这个样本被分错的概率是1-Pk,同样的，我们根据基尼指数计算基尼信息增益。这里引入一个心的概念——信息增益（信息增益：某个分割前后数据的熵的减少量称为信息增益）

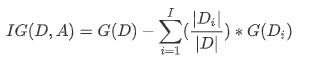
其中，数据集D按照条件A划分成了I个类别，|Di|表示第i类别中的样本数，|D|表示总体的样本数。G(D)代表整个数据集的基尼指数，G(Di)代表第i类别样本的基尼指数。

理论显得枯燥乏味，下面举例说明：
还记得Mike的选择吗？我们将数据集整理如下：

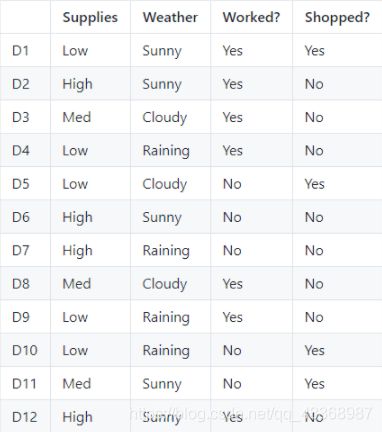
1. 首先，我们知道整个数据集的决策是是否去购物。
2. 在所有的12中选择中，最终去购物有4种情况，不去购物有8种情况，那么总体的基尼指数应该为：

3. G(shopped)=1-((4/12)²+(8/12)²)				
   

4. G(shopped)=0.44
   

5. 现在我们来拆分第一个因素：物品的供应量，我们可以根据物品的供应量分成三个类别：高，中，低
6. 针对每个类别，根据上图数据，我们计算出其基尼指数：

7. G(Low)=1-((3/5)²+(2/5)²)=0.48	
   

8. G(Med)=1-((1/3)²+(2/3)²)=0.44	
   

9. G(High)=1-((0/4)²+(4/4)²)=0
   

10. 所以我们可以计算出此次分割的基尼信息增益为：
    

11.    IG(shopped,supplies)=0.44-(5/12*0.48+3/12*0.44+4/12*0)=0.133
    

12. 我们可以一直重复这种操作，直到做出最优化分为止

五、剪枝

决策树算法在学习的过程中为了尽可能的正确的分类训练样本，会不停地对节点进行划分。因此这会导致整棵树的分支过多，也就会出现过拟合的现象。所以修剪决策树中比较不太重要的分支是有用的。常见的兼职策略有两种：
预剪枝：
预剪枝就是在构造决策树的过程中，先对每个节点在划分前后进行估计。如果当前节点的划分不能带来决策树模型泛化性能的提升，则不对当前节点进行划分并且将当前节点标记为叶结点
后剪枝：
后剪枝就是先把整棵决策树构造完毕，然后自底向上的对非叶节点进行考察。若将该结点对应的子树换为叶结点能够带来泛化性能的提升，则把该子树替换为叶节点

六、代码实现

# 决策树
import graphviz
import itertools
import random
from sklearn.tree import DecisionTreeClassifier,export_graphviz
from sklearn.preprocessing import OneHotEncoder

# 为每个特征创建不同的特征值作为分类
classes={
     
    'supplies':['low','med','high'],
    'weather':['raining','cloudy','sunny'],
    'worked':['yes','no']
}
# 创建数据集
data=[
    ['low',  'sunny',   'yes'],
    ['high', 'sunny',   'yes'],
    ['med',  'cloudy',  'yes'],
    ['low',  'raining', 'yes'],
    ['low',  'cloudy',  'no' ],
    ['high', 'sunny',   'no' ],
    ['high', 'raining', 'no' ],
    ['med',  'cloudy',  'yes'],
    ['low',  'raining', 'yes'],
    ['low',  'raining', 'no' ],
    ['med',  'sunny',   'no' ],
    ['high', 'sunny',   'yes']
]
# 创建不同的决策结果
target=['yes', 'no', 'no', 'no', 'yes', 'no', 'no', 'no', 'no', 'yes', 'yes', 'no']
# sklearn 无法直接处理字符串类型的数据，所以要将数据重新编码，采取onehot编码
# onehot编码又称为一位有效编码，主要是采用N位状态寄存器来对N个状态进行编码，每个状态都有他独立的寄存器位，并且在任意时候只有一位有效
# onehot编码是分类变量作为二进制向量的表示，这首先要求将分类值映射到整数值，然后，每个整数值被表示为二进制向量，除了整数的索引之外，他都是零值，他被标记为1

# 将分类转换成onehot
categories=[classes['supplies'],classes['weather'],classes['worked']]
encoder=OneHotEncoder(categories=categories)
# 用onehot编码转换数据集
x_data=encoder.fit_transform(data)
# 用给定的数据集训练决策树的模型
classifier=DecisionTreeClassifier()
tree=classifier.fit(x_data,target)
prediction_data=[]
# 随机创建五条三种特征的条件
for _ in itertools.repeat(None,5):
    prediction_data.append([
        random.choice(classes['supplies']),
        random.choice(classes['weather']),
        random.choice(classes['worked'])
    ])
# 运用决策树模型，预测最终结果
prediction_result=tree.predict(encoder.transform(prediction_data))
# 输出结果
# print(prediction_result)

# 为方便阅读，将结果格式化输出
def format_array(arr):
    return ''.join(['|{:<10}'.format(item) for item in arr])
def print_table(data,result):
    line='day  '+format_array(list(classes.keys())+['go shopping?'])
    print('-'*len(line))
    print(line)
    print('-'*len(line))
    for day,row in enumerate(data):
        print('{:<5}'.format(day+1)+format_array(row+[result[day]]))
    print('')
# 训练数据集
print('训练数据：')
print_table(data,target)
# 预测结果
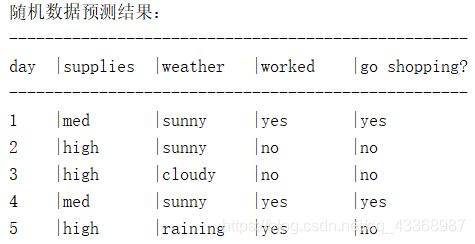
print('随机数据预测结果：')
print_table(prediction_data,prediction_result)

运行结果

七、小结

决策树可以非常快速有效的对数据进行分类，而且算法的实现过程也很容易理解。决策树的创建和优化是经过两个过程所完成的：分裂和修剪。分裂选择最佳的特征对其进行拆分，而修剪则可以过滤掉无用的枝叶，带来性能的提升。由于决策树的创建和理解十分容易，所以常常被用来作为机器学习的首选算法。

自学自用，希望可以和大家积极沟通交流，小伙伴们加油鸭，如有错误还请指正，不喜勿喷，喜欢的小伙伴帮忙点个赞支持，蟹蟹呀