动手学深度学习PyTorch版——Task01学习笔记
线性回归
线性回归模型从零开始
# 引入需要的包和模块
%matplotlib inline
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
print(torch.__version__)
# 使用线性模型来生成数据集,生成一个1000个样本的数据集
#设置输入特征数量,两个特征
num_inputs = 2
#设置样本数量
num_examples = 1000
#设置真实的权重和偏差以生成相应的标签
true_w = [2,-3.4]
true_b = 4.2
features = torch.randn(num_examples,num_inputs,dtype=torch.float32) #1000*2的矢量
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b
labels += torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float32) #通过正态分布随机生成偏差
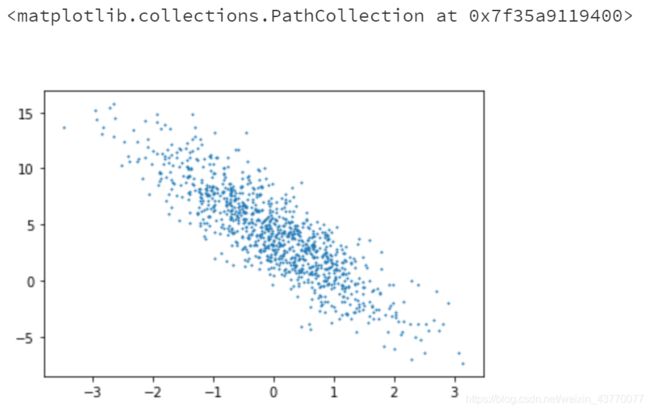
# 使用图像来展示生成的数据
plt.scatter(features[:,1].numpy(),labels.numpy(),1)
# 读取数据集
def data_iter(batch_size,features,labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) #随机读取10个样本
for i in range(0,num_examples,batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size,num_examples)]) #最后一次可能不足以整个批次
yield features.index_select(0,j),labels.index_select(0,j)
batch_size = 10
for X,y in data_iter(batch_size,features,labels):
print(X,'\n',y)
break
# 初始化模型参数
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
w.requires_grad_(requires_grad=True) #梯度的附加操作
b.requires_grad_(requires_grad=True)
def linreg(X,w,b):
return torch.mm(X,w) + b
# 定义损失函数(均方误差损失函数)
def squared_loss(y_hat,y):
return (y_hat - y.view(y_hat.size())) ** 2 / 2
# 定义优化函数(小批量随机梯度下降)
def sgd(params,lr,batch_size):
for param in params:
param.data -= lr * param.grad / batch_size #使用.data可以在没有渐变轨迹的情况下操作参数
# 训练
#超参数初始化,超参数是需要人为设置的参数
lr = 0.03 #学习率
num_epochs = 5 #训练周期
net = linreg
loss = squared_loss
#训练
for epoch in range(num_epochs): #训练重复num_epochs次
#每个epoch中,所有在数据集中的样本都被使用一次
#X是特征,y是批量样本的标签
for X,y in data_iter(batch_size,features,labels):
l = loss(net(X,w,b),y).sum()
#计算批量样本损失的梯度
l.backward()
#使用小批量随机梯度下降迭代模型参数
sgd([w,b],lr,batch_size)
#重置参数梯度
w.grad.data.zero_() #参数梯度清零,防止参数累加
b.grad.data.zero_()
train_l = loss(net(features,w,b),labels)
print('epoch %d,loss %f' % (epoch + 1,train_l.mean().item()))
w,true_w,b,true_b
线性回归模型的pytorch实现
import torch
from torch import nn
import numpy as np
torch.manual_seed(1)
print(torch.__version__)
torch.set_default_tensor_type('torch.FloatTensor')
# 生成数据集
num_inputs = 2
num_examples = 1000
true_w = [2,-3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
# 读取数据
import torch.utils.data as Data
batch_size = 10
# 结合数据集的特征和标签
dataset = Data.TensorDataset(features, labels)
# 将数据集放入DataLoader
data_iter = Data.DataLoader(
dataset=dataset, # torch TensorDataset format
batch_size=batch_size, # 小批量的大小
shuffle=True, # 是否随机读取数据
num_workers=2, # 在多线程中读数据
)
for X, y in data_iter:
print(X, '\n', y)
break
# 定义模型
class LinearNet(nn.Module):
def __init__(self,n_features):
super(LinearNet,self).__init__() #调用父函数来初始化
self.linear = nn.Linear(n_features,1)
def forward(self,x):
y = self.linear(x)
return y
net = LinearNet(num_inputs)
print(net)
#初始化多层神经网络的方法
#方法一
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# 其它层在这里加
)
# 方法二
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......
# 方法三
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
('linear', nn.Linear(num_inputs, 1))
# ......
]))
print(net)
print(net[0])
#初始化模型参数
from torch.nn import init
init.normal_(net[0].weight, mean=0.0, std=0.01)
init.constant_(net[0].bias, val=0.0)
# 定义损失函数
loss = nn.MSELoss()
#定义优化函数
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03) # 内置随机梯度下降函数
print(optimizer)
# 训练
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X)
l = loss(output, y.view(-1, 1))
optimizer.zero_grad() # 重置梯度,相当于net.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss: %f' % (epoch, l.item()))
# 结果比较
dense = net[0]
print(true_w, dense.weight.data)
print(true_b, dense.bias.data)
学习笔记
线性回归的基本要素:训练模型,训练集,优化函数,损失函数。
线性回归的训练模型为线性模型,训练集即为数据集,优化函数为小批量的梯度下降,损失函数为均方误差。
pytorch内的函数
☛torch.ones()/torch.zeros(),与MATLAB的ones/zeros很接近。初始化生成
均匀分布
☛torch.rand(*sizes, out=None) → Tensor
返回一个张量,包含了从区间[0, 1)的均匀分布中抽取的一组随机数。张量的形状由参数sizes定义。
标准正态分布
☛torch.randn(*sizes, out=None) → Tensor
返回一个张量,包含了从标准正态分布(均值为0,方差为1,即高斯白噪声)中抽取的一组随机数。张量的形状由参数sizes定义。
☛torch.mul(a, b)是矩阵a和b对应位相乘,a和b的维度必须相等,比如a的维度是(1, 2),b的维度是(1, 2),返回的仍是(1, 2)的矩阵
☛torch.mm(a, b)是矩阵a和b矩阵相乘,比如a的维度是(1, 2),b的维度是(2, 3),返回的就是(1, 3)的矩阵
☛torch.Tensor是一种包含单一数据类型元素的多维矩阵,定义了7种CPU tensor和8种GPU tensor类型。
☛random.shuffle(a):用于将一个列表中的元素打乱。shuffle() 是不能直接访问的,需要导入 random 模块,然后通过 random 静态对象调用该方法。
☛*backward()*是pytorch中提供的函数,配套有require_grad:
1.所有的tensor都有.requires_grad属性,可以设置这个属性.x = tensor.ones(2,4,requires_grad=True)
2.如果想改变这个属性,就调用tensor.requires_grad_()方法: x.requires_grad_(False)
实现顺序
1.生成数据集
随机标签,指定参数,计算标准结果添加噪声
2.定义模型
3.定义损失函数
4.定义优化模型
5.训练模型
1)设置超参,初始化模型参数
2)每次迭代中,小批量读取数据,初始化模型计算预测值,损失函数计算插值,反向传播求梯度,优化算法更新参数,参数梯度清零
softmax与分类模型
softmax回归模型的从零开始实现
# 导入所需要的包和模块
import torch
import torchvision
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)
print(torchvision.__version__)
# 获取训练集和测试数据集
batch_size = 256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size,root="/home/kesci/input/FashionMNIST2065")
# 模型参数初始化
num_inputs = 784
print(28 * 28)
num_outputs = 10
w = torch.tensor(np.random.normal(0 , 0.01, (num_inputs, num_outputs)),dtype=torch.float)
b = torch.zeros(num_outputs, dtype=torch.float)
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
# 对多维tensor按维度操作
X = torch.tensor([[1,2,3], [4,5,6]])
print(X.sum(dim=0, keepdim=True)) #dim=0,按照相同的列求和,并在结果中保留列的特征
print(X.sum(dim=1, keepdim=True)) #dim=1,按照相同的行求和
#定义softmax操作
def softmax(X):
X_exp = X.exp()
partition = X_exp.sum(dim=1,keepdim=True)
#print("X size is ",X_exp.size())
#print("partition size is ",partition,partition.size())
return X_exp / partition #这里使用了广播机制
X = torch.rand((2, 5))
X_prob = softmax(X)
print(X_prob, '\n', X_prob.sum(dim=1))
#softmax的回归模型
def net(X):
return softmax(torch.mm(X.view((-1, num_inputs)), w) + b)
# 定义损失函数
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = torch.LongTensor([0, 2])
y_hat.garther(1, y.view(-1, 1))
#定义准确率
def accuracy(y_hat, y):
return (y_hat.argmax(dim=1) == y).float().mean().item()
print(accuracy(y_hat,y))
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().iter()
n += y.shape[0]
return acc_sum / n
print(evaluate_accuracy(data_iter, net))
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
d2l.sgd(params, lr, batch_size)
else:
optimizer.step()
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)
#模型预测
X, y = iter(test_iter).next()
true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [true + '\n' +pred for true,pred in zip(true_labels, pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])
softmax回归模型pytorch实现
# 加载各种包或者模块
import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)
# 初始化参数和获取数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, root='/home/kesci/input/FashionMNIST2065')
# 定义网络模型
num_inputs = 784
num_outputs = 10
class LinearNet(nn.Module):
def __init__(self, num_inputs, num_outputs):
super(LinearNet, self).__init__()
self.linear = nn.Linear(num_inputs, num_outputs)
def forward(self, x): # x 的形状: (batch, 1, 28, 28)
y = self.linear(x.view(x.shape[0], -1))
return y
# net = LinearNet(num_inputs, num_outputs)
class FlattenLayer(nn.Module):
def __init__(self):
super(FlattenLayer, self).__init__()
def forward(self, x): # x 的形状: (batch, *, *, ...)
return x.view(x.shape[0], -1)
from collections import OrderedDict
net = nn.Sequential(
# FlattenLayer(),
# LinearNet(num_inputs, num_outputs)
OrderedDict([
('flatten', FlattenLayer()),
('linear', nn.Linear(num_inputs, num_outputs))]) # 或者写成我们自己定义的 LinearNet(num_inputs, num_outputs) 也可以
)
# 初始化模型参数
init.normal_(net.linear.weight, mean=0, std=0.01)
init.constant_(net.linear.bias, val=0)
#定义损失函数
loss = nn.CrossEntropyLoss() # 下面是他的函数原型
# class torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')
# 定义优化函数
optimizer = torch.optim.SGD(net.parameters(), lr=0.1) # 下面是函数原型
# class torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)
num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)
学习笔记
线性回归:预测连续值,损失函数通常用均方根
SoftMax回归:预测离散值,用于分类,损失函数通常用交叉熵,softMax这一步主要用于归一化,得到概率分布
SoftMax对输出层进行归一化的原因:
1、输出层的输出值的范围不确定,难以直观上判断这些值的意义。
2、由于真实标签是离散值,这些离散值与不确定范围的输出值之间的误差难以衡量。
交叉熵损失函数: 只考虑正确类别的预测概率
多层感知机
多层感知机图像分类的从零开始的实现
import torch
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)
#获取训练集
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,root='/home/kesci/input/FashionMNIST2065')
#定义模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_hiddens)), dtype=torch.float)
b1 = torch.zeros(num_hiddens, dtype=torch.float)
W2 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens, num_outputs)), dtype=torch.float)
b2 = torch.zeros(num_outputs, dtype=torch.float)
params = [W1, b1, W2, b2]
for param in params:
param.requires_grad_(requires_grad=True)
#定义激活函数
def relu(X):
return torch.max(input=X, other=torch.tensor(0.0))
#定义网络
def net(X):
X = X.view((-1, num_inputs))
H = relu(torch.matmul(X, W1) + b1)
return torch.matmul(H, W2) + b2
#定义损失函数
loss = torch.nn.CrossEntropyLoss()
#训练
# def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
# params=None, lr=None, optimizer=None):
# for epoch in range(num_epochs):
# train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
# for X, y in train_iter:
# y_hat = net(X)
# l = loss(y_hat, y).sum()
#
# # 梯度清零
# if optimizer is not None:
# optimizer.zero_grad()
# elif params is not None and params[0].grad is not None:
# for param in params:
# param.grad.data.zero_()
#
# l.backward()
# if optimizer is None:
# d2l.sgd(params, lr, batch_size)
# else:
# optimizer.step() # “softmax回归的简洁实现”一节将用到
#
#
# train_l_sum += l.item()
# train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
# n += y.shape[0]
# test_acc = evaluate_accuracy(test_iter, net)
# print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
# % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)
多层感知机pytorch实现
import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("/home/kesci/input")
import d2lzh1981 as d2l
print(torch.__version__)
#初始化模型和各个参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256
net = nn.Sequential(
d2l.FlattenLayer(),
nn.Linear(num_inputs, num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens, num_outputs),
)
for params in net.parameters():
init.normal_(params, mean=0, std=0.01)
#训练
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,root='/home/kesci/input/FashionMNIST2065')
loss = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)
学习笔记
线性回归和softmax回归是单层神经网络,多层感知机是多层神经网络
隐藏层:多层感知机在单层神经网络的基础上引入了一道多的隐藏层,位于输入层和输出层之间。
层感知机中的隐藏层和输出层都是全连接层。
多层感知机:含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出通过记过函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。
激活函数:非线性变换
- ReLU函数
ReLU(rectified linear unit)函数提供了一个很简单的非线性变换。给定元素x,该函数定义为
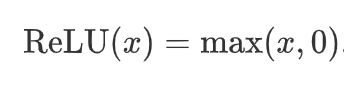
- Sigmoid函数
sigmoid函数可以将元素的值变换到0和1之间:
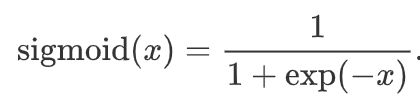
- tanh函数
tanh(双曲正切)函数可以将元素的值变换到-1和1之间:

关于激活函数的选择
☛ReLu函数是一个通用的激活函数,目前在大多数情况下使用。但是,ReLU函数只能在隐藏层中使用。
☛用于分类器时,sigmoid函数及其组合通常效果更好。由于梯度消失问题,有时要避免使用sigmoid和tanh函数。
☛在神经网络层数较多的时候,最好使用ReLu函数,ReLu函数比较简单计算量少,而sigmoid和tanh函数计算量大很多。
☛在选择激活函数的时候可以先选用ReLu函数如果效果不理想可以尝试其他激活函数。