聚类算法之DBSCAN

DBSCAN聚类算法

1. DBSCAN算法基本概念

DBSCAN是一种典型的基于密度的聚类算法，基于一组邻域$(ϵ,MinPts)$来描述样本集的紧密程度。其中$ϵ$描述了某一样本的邻域距离阈值，$MinPts$描述了某一样本的距离为$ϵ$的邻域中样本个数的阈值。

在DBSCAN算法中将数据点分为以下三类：

• 核心点：若样本$x_i$的$ϵ$邻域内至少包含$MinPts$样本，即$|N_{ϵ}(x_i)|\ge MinPts$，则称样本点$x_i$为核心点
• 边界点：若样本点$x_i$的$ϵ$邻域内包含的样本数目小于$MinPts$，但是它在其他核心点的邻域内，则称样本点$x_i$为边界点
• 噪音点：既不是核心点也不是边界点的点

在DBSCAN算法中还定义了如下概念：

• 密度直达：若样本点$x_j$在核心点$x_i$的$ϵ$邻域内，则称样本点$x_j$由$x_i$密度直达。
• 密度可达：若在样本点$x_{i,1}$和样本点$x_{i,n}$之间存在序列$x_{i,2},...,x_{i,n-1}$，且$x_{i,j+1}$由$x_{i,j}$密度直达，则称$x_{i,n}$由$x_{i,1}$密度可达。由密度直达的定义可知，样本点$x_{i,1},x_{i,2},...,x_{i,n-1}$均为核心点
• 密度连接：对于样本点$x_i$和样本点$x_j$，若存在样本点$x_k$，使得$x_i$和$x_j$都由$x_k$密度可达，则称$x_i$和$x_j$密度相连

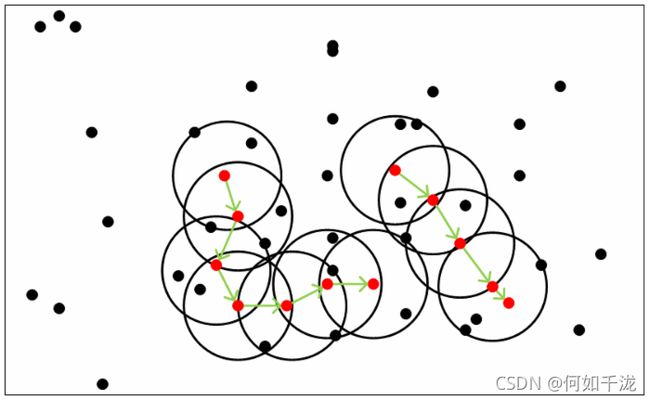
上图$MinPts=5$，红色的样本都是核心点，因为其$ϵ$邻域至少有5个样本。黑色的样本是非核心点，其中红色样本邻域内的黑色样本为边界点，其他黑色样本为噪音点。所有核心点密度直达的样本在以红色样本为中心的超球体内，如果不在超球体内，则不能密度直达。图中用绿色箭头连起来的核心点组成了密度可达的样本序列。在这些密度可达的样本序列的$ϵ$邻域内所有的样本相互都是密度相连的。

2. DBSCAN聚类算法流程

$输入：样本集D=\{x_1,x_2,...,x_n\}，邻域参数(ϵ,MinPts)，样本距离度量方式$

$输出：簇划分C=\{C_1,C_2,...,C_k\}$

1. 初始化核心点集合$\Omega =\varnothing$，初始化聚类簇数$k=0$，初始化为访问集合$\Gamma =D$，簇划分$C=\varnothing$

2. 对于$i=1,2,...,n$，按下面步骤找出所有的核心点：

   • 通过距离度量方式，找到样本$x_i$的$ϵ$邻域子样本集$N_{ϵ}(x_i)$
   • 如果子样本集样本个数满足$|N_{ϵ}(x_i)|\ge MinPts$，将样本$x_i$加入核心点集合：$\Omega =\Omega \cup \{x_i\}$

3. 如果核心点集合$\Omega =\varnothing$，结束，否则转入步骤4

4. 在核心点集合$\Omega$中，随机选择一个核心点$o$，初始化当前簇核心点队列${\Omega }_{cur}=\{o\}$，初始化类别序号$k=k+1$，初始化当前簇样本集合$C_k=\{o\}$，更新为访问样本集合$\Gamma =\Gamma -\{o\}$

5. 如果当前核心点队列${\Omega }_{cur}=\varnothing$，则当前簇$C_k$生成完毕，更新簇划分$C=\{C_1,C_2,...,C_k\}$，更新核心点集合$\Omega =\Omega -C_k$，转入步骤3。否则更新核心点集合$\Omega =\Omega -C_k$

6. 在当前簇核心点队列${\Omega }_{cur}$中取出一个核心点$o^{\prime }$，通过邻域阈值$ϵ$找出所有的$ϵ$邻域子样本集$N_{ϵ}(o^{\prime })$，令$\Delta =N_{ϵ}(o^{\prime })\cap \Gamma$，更新当前簇样本集合$C_k=C_k\cup \Delta$，更新为访问样本集合$\Gamma =\Gamma -\Delta$，更新${\Omega }_{cur}={\Omega }_{cur}\cup (\Delta \cap \Omega )-\{o^{\prime }\}$，转入步骤5

简单来说：

1. 根据给定的邻域参数$ϵ$和$MinPts$确定所有的核心点
2. 对每一个核心点
3. 选择一个未处理过的核心点，找到由其密度可达的样本生成聚类‘簇’
4. 重复以上过程

3. 实例演示

import numpy as np 
import matplotlib.pyplot as plt 

from sklearn import cluster, datasets
from sklearn.preprocessing import StandardScaler

np.random.seed(0)

# 构建数据
n_samples = 1500
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)

data_sets = [
    (
        noisy_circles,
        {
     
            "eps": 0.3,
            "min_samples": 5
        }
    ),
    (
        noisy_moons,
        {
     
            "eps": 0.3, 
            "min_samples": 5
        }
    ), 
    (
        blobs, 
        {
     
            "eps": 0.3, 
            "min_samples": 5
        }
    )
]
colors = ["#377eb8", "#ff7f00", "#4daf4a"]

plt.figure(figsize=(15, 5))

for i_dataset, (dataset, algo_params) in enumerate(data_sets):
    # 模型参数
    params = algo_params

    # 数据
    X, y = dataset
    X = StandardScaler().fit_transform(X)

    # 创建DBSCAN
    dbscan = cluster.DBSCAN(eps=params["eps"], min_samples=params['min_samples'])

    # 训练
    dbscan.fit(X)

    # 预测
    y_pred = dbscan.labels_.astype(int)

    y_pred_colors = []

    for i in y_pred:
        y_pred_colors.append(colors[i])
    
    plt.subplot(1, 3, i_dataset+1)

    plt.scatter(X[:, 0], X[:, 1], color=y_pred_colors)

plt.show()

4. DBSCAN小结

优点：

1. 可以对任意形状的稠密数据集进行聚类，相对的，K-Means、Mean Shift之类的聚类算法一般只适用于凸数据集
2. 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。
3. 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

缺点：

1. 如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。
2. 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
3. 调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值$ϵ$，邻域样本数阈值$MinPts$联合调参，不同的参数组合对最后的聚类效果有较大影响。