MCMC和Gibbs Sampling
很多常见的概率分布,都可以用 U n i f o r m ( 0 , 1 ) Uniform(0, 1) Uniform(0,1)的样本生成,比如正态分布:

但是,如果某个分布过于复杂,样本的生成就很困难了。于是我们需要更加复杂的随机模拟方法生成样本。MCMC采样和gibbs sampling就是常用的一种。介绍这两个算法前,需要有一些马氏链的基本知识。
马尔科夫链
马尔可夫链又称离散时间马尔可夫链,为状态空间中经过从一个状态到另一个状态转换的随机过程。
该过程要求具有“无记忆”的性质:下一个状态的概率分布只能由当前状态来决定,在时间序列中前面的事件均与之无关。这种特定的 无记忆性 被称作马尔可夫性质。
用数学的方式来表达:假设状态序列为 x 1 , x 2 , ⋯ , x t − 1 , x t , x t + 1 , ⋯ x_1,x_2,\cdots,x_{t-1},x_t,x_{t+1},\cdots x1,x2,⋯,xt−1,xt,xt+1,⋯,由马尔可夫链定义知,时刻t+1的状态只与时刻t的状态有关,则有:
P ( x t + 1 ∣ x 1 , x 2 , ⋯ ) = P ( x t + 1 ∣ x t ) P(x_{t+1}|x_1,x_2,\cdots)=P(x_{t+1}|x_t) P(xt+1∣x1,x2,⋯)=P(xt+1∣xt)
由于下一个状态只与当前状态有关,因此,只要求得到两个状态之间的转移概率(又称状态转移矩阵),即可得到一个马尔可夫链模型。
举个例子:

的状态转移矩阵为:

如果我们对其不断的求幂,我们会发现它会收敛:
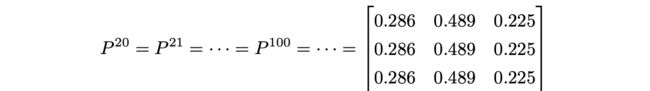
关于马氏链的平稳分布我们有如下定理:

细致平衡条件
什么样的状态转移矩阵能够使得马氏链达到平稳分布呢?
细致平衡条件(Detailed Balance Condition):给定一个马尔可夫链,分布 π \pi π和概率矩阵 P P P,如果下面等式成立:
π i P i j = π j P j i \pi_iP_{ij}=\pi_jP_{ji} πiPij=πjPji
则称马尔可夫链具有平稳分布(Stationary Distribution)。
细致平衡条件是马氏链收敛的充分条件。
简单给出证明:
如果满足平稳分布,则根据定理0.4.2有:
π i = ∑ j π j P j i \pi_i=\sum_j \pi_jP_{ji} πi=j∑πjPji
我们对等式右边进行变换:
∑ j π j P j i = ∑ j π i P j i = π i ∑ j P j i = π i \sum_j \pi_jP_{ji} = \sum_{j}\pi_i P_{ji}=\pi_i \sum_jP_{ji}=\pi_i j∑πjPji=j∑πiPji=πij∑Pji=πi
证明成立。
MCMC
对于给定的概率分布 p ( x ) p(x) p(x),我们希望能有便捷的方式生成它对应的随机样本。一个想法是,如果有一个马氏链的平稳分布恰恰是 p ( x ) p(x) p(x),就可以根据任何初始状态最终收敛于平稳分布。
假设有一个状态转移矩阵是 Q Q Q,通常情况下:
p ( i ) q ( i , j ) ≠ p ( j ) q ( j , i ) p(i)q(i,j)≠p(j)q(j,i) p(i)q(i,j)=p(j)q(j,i)
细致平衡条件不成立,我们对其稍作修改,使之满足细致平衡条件:
p ( i ) q ( i , j ) α ( i , j ) = p ( j ) q ( j , i ) α ( j , i ) p(i)q(i,j)\alpha(i,j)=p(j)q(j,i)\alpha(j,i) p(i)q(i,j)α(i,j)=p(j)q(j,i)α(j,i)
其中:
α ( i , j ) = p ( j ) q ( j , i ) , α ( j , i ) = p ( i ) q ( i , j ) \alpha(i,j)=p(j)q(j,i),\alpha(j,i)=p(i)q(i,j) α(i,j)=p(j)q(j,i),α(j,i)=p(i)q(i,j)
此时,细致平稳分布就成立了。
我们把 α ( i , j ) \alpha(i,j) α(i,j)称为接受率,如下图所示:
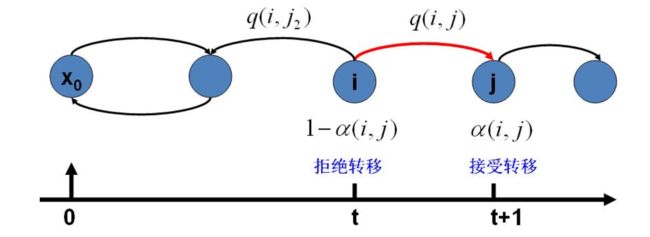
根据上述分析,我们就可以得到一个采样概率分布 p ( x ) p(x) p(x)的算法:

但是,这个算法收敛的比较慢,因为 α ( i , j ) \alpha(i,j) α(i,j)较小,大部分时间在原地踏步,所以我们可以针对 α ( i , j ) \alpha(i,j) α(i,j)进行一些改进:
对 p ( i ) q ( i , j ) α ( i , j ) = p ( j ) q ( j , i ) α ( j , i ) p(i)q(i,j)\alpha(i,j)=p(j)q(j,i)\alpha(j,i) p(i)q(i,j)α(i,j)=p(j)q(j,i)α(j,i)而言,左右两边同时扩大N倍,等式同样成立,因此,将两数中大的那个数放大到1,会大幅提高接受度,其改进后的公式如下:

于是,我们得到Metropolis-Hastings算法:

Gibbs Sampling
对于高维的情形,由于接受率的存在,Metropolis-Hastings的算法效率仍不够高,我们希望找到一个转移矩阵 Q Q Q使得接受率为1。那么应该怎么做呢?首先来看二维的情形:
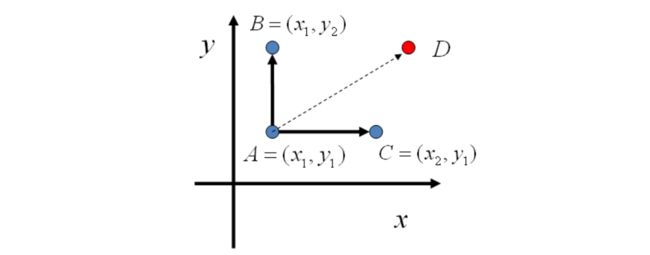
假设有一个概率分布 p ( x , y ) p(x,y) p(x,y),对于A,B两个点,我们有:
p ( x 1 , y 1 ) p ( y 2 ∣ x 1 ) = p ( x 1 , y 1 , y 2 ) p ( x 1 , y 2 ) p ( y 1 ∣ x 1 ) = p ( x 1 , y 1 , y 2 ) ⇒ p ( x 1 , y 1 ) p ( y 2 ∣ x 1 ) = p ( x 1 , y 2 ) p ( y 1 ∣ x 1 ) p(x_1,y_1)p(y_2|x_1)=p(x_1,y_1,y_2) \\ p(x_1,y_2)p(y_1|x_1)=p(x_1,y_1,y_2) \\ ⇒ p(x_1,y_1)p(y_2|x_1)=p(x_1,y_2)p(y_1|x_1) p(x1,y1)p(y2∣x1)=p(x1,y1,y2)p(x1,y2)p(y1∣x1)=p(x1,y1,y2)⇒p(x1,y1)p(y2∣x1)=p(x1,y2)p(y1∣x1)
同样的,对于具有某个相同坐标的A,C也具有相同的性质。因此,我们可以得出:如果马氏链的转移是沿着坐标轴做转移,那么满足细致平衡条件。以下是二维吉布斯采样中的马氏链转移图:
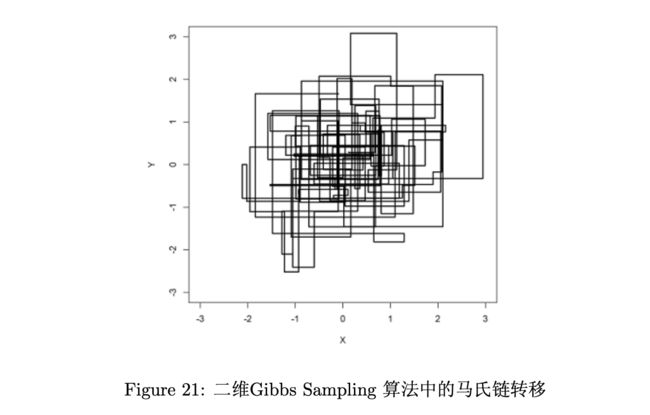
如果将问题扩散到高维,也很容易可以得出:
p ( x ⃗ 1 , y 1 ) p ( y 2 ∣ x ⃗ 1 ) = p ( x ⃗ 1 , y 2 ) p ( y 1 ∣ x ⃗ 1 ) p(\vec x_1,y_1)p(y_2|\vec x_1)=p(\vec x_1,y_2)p(y_1|\vec x_1) p(x1,y1)p(y2∣x1)=p(x1,y2)p(y1∣x1)
同样满足细致平衡条件。
因此我们可以得出高维的吉布斯采样的算法:

参考
LDA 数学八卦